Play Freedom Trail with DP

The cover image of this article is from a mission storyline in a game called "Fallout 4":

This rotating disk resembles a combination lock. Notice the red pointer slightly above the center. By rotating the disk, you can align the pointer with different letters and then press the central button to input the selected letter.

To trigger the mechanism and open the adjacent door, you need to rotate the disk so the pointer successively points to R, A, I, L, R, O, A, D, pressing the button each time.

The reason these specific letters form the password is hinted at in the game's storyline, which we won't delve into here.

So, what does this game scenario have to do with dynamic programming?

Let's think about it a bit: inputting these letters by rotating the disk can be cumbersome. In what sequence should you rotate the disk to minimize the number of moves required?

The number of moves required will vary depending on the method used to rotate the disk.

For instance, to align a letter with the pointer, you can rotate the disk clockwise or counterclockwise. Some letters may appear more than once, such as the uppercase letter O in the image, which appears three times at different positions on the disk. Which O should you align with to minimize the total number of moves?

As we've mentioned several times before, problems that ask for the optimal solution are typically solved using dynamic programming, as it is a type of optimization algorithm.

There's a problem on LeetCode based on this disk game, and it's rated Hard. However, I solved it quickly because I had previously considered a very interesting real-life example that can be compared to this problem. Let's briefly introduce it below.

I once practiced several piano pieces by Liszt and Chopin. Readers who haven't played the piano might not know that practicing piano scores requires determining the "fingerings" in advance.

The notes on the staff go up and down, and the fingers of both hands must coordinate with each other. This means you must decide which finger of which hand to use for each note and write it on the score.

For example, a piece I really like is called "Liebestraum," and here is the score from when I was a beginner:

The number 1 on the notes represents the thumb, 2 represents the index finger, and so on. By practicing according to the determined fingerings, you develop muscle memory and eventually master a piece.

Fingerings vary from person to person. For instance, those with larger hands might be able to cross their middle finger over their thumb, while those with smaller hands might find this awkward. Thus, the fingerings for the same piece might differ.

So the question arises: How should I design the fingerings to minimize the "awkwardness" of finger transitions, thereby maximizing the smoothness of the performance?

Here, I employed dynamic programming techniques: aren't finger transitions just state transitions? Referring to the earlier article Detailed Explanation of Dynamic Programming, we can solve this problem by clearly defining "states" and "choices."

What is a state? A state is "the next note to be played" and "the current state of the hand."

The next note to be played is simply one of the 88 keys on the piano. The state of the hand is also straightforward: with five fingers, each finger is either pressing a key or not. This results in 32 possible situations, represented by 5 binary digits.

What is a choice? A choice is "which finger should play the next note," which involves simply considering all five fingers.

Of course, considering the current state of the hand, each choice comes with a corresponding cost. As mentioned earlier, this cost varies from person to person, so I need to design a custom loss function for myself to calculate the "awkwardness level" of different finger transitions.

The problem now becomes a standard dynamic programming problem: make the choices that result in the minimum "awkwardness level" according to the loss function to ensure the smoothest performance...

However, the time complexity of this algorithm is too high. We only analyzed a single note earlier, but if we string them into a piece, the time and space complexity must be multiplied by the number of notes in the piece, which is significant.

Moreover, this loss function is difficult to quantify. Hitting the black and white keys on a piano varies in difficulty, and the "awkwardness level" is based on feeling, which is somewhat imprecise...

However, there is no need to calculate the fingering for the entire piece; only certain complex passages need to be considered. This algorithm is still relatively effective.

Having digressed so much, it is finally time to get to the main topic. Today, we will discuss LeetCode Problem 514, "Freedom Trail," which has a similar concept to the piano fingering problem. If you understand the piano example, you should be able to solve this algorithm problem quickly.

The problem provides you with an input string ring representing the characters on a dial (the pointer is at the 12 o'clock position, initially pointing to ring[0]), and another input string key representing the string you need to type by rotating the dial. Your algorithm needs to return the minimum number of operations required to input this key (rotating one notch of the dial and pressing the button in the center of the dial both count as one operation).

The function signature is as follows:

int findRotateSteps(String ring, String key);

int findRotateSteps(string ring, string key);

def findRotateSteps(ring: str, key: str) -> int:

func findRotateSteps(ring string, key string) int {}

var findRotateSteps = function(ring, key) {}

For example, given the input ring = "godding", key = "gd", the corresponding disk is shown below (uppercase is for clarity, the actual input strings are lowercase letters):

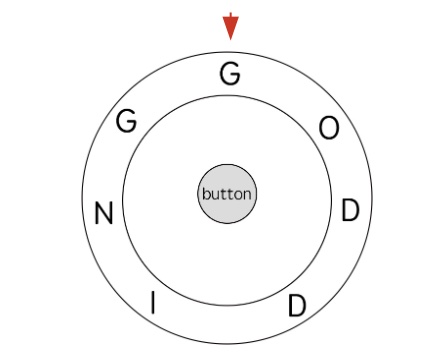
We need to input key = "gd", and the algorithm returns 4.

Since the pointer is currently on the letter "g", you can press the middle button directly, then rotate the disk two steps counterclockwise so that the pointer points to the letter "d", and press the middle button again.

In this process, the button is pressed twice, and the disk is rotated two steps, totaling 4 operations, which is the minimum number of operations, so the algorithm should return 4.

We can first make an equivalence in the problem: is rotating the disk equivalent to moving the pointer?

The original problem can be transformed into: the disk is fixed, and we can move the pointer; now we need to move the pointer and press the button to input the string corresponding to key with the fewest operations.

So, how can we solve this problem using dynamic programming techniques? Or rather, what are the "states" and "choices" in this problem?

The "state" is "the current character to be input" and "the current position of the disk pointer."

More specifically, the "state" is represented by two variables i and j. We can use i to represent the character that the pointer on the current disk is pointing to (i.e., ring[i]); j represents the character to be input (i.e., key[j]).

Thus, we can write a dp function:

int dp(String ring, int i, String key, int j);

int dp(string ring, int i, string key, int j);

def dp(ring: str, i: int, key: str, j: int) -> int:

func dp(ring string, i int, key string, j int) int

var dp = function(ring, i, key, j){}

The dp function is defined as follows:

When the disk pointer points to ring[i], at least dp(ring, i, key, j) operations are needed to input the string key[j..].

According to this definition, the problem is essentially asking to calculate the value of dp(ring, 0, key, 0), and we can write the base case of the dp function:

int dp(String ring, int i, String key, int j) {
    // base case, input is complete
    if (j == key.length()) return 0;
    // ...
}

int dp(string ring, int i, string key, int j) {
    // base case, input is completed
    if (j == key.length()) return 0;
    // ...
}

def dp(ring: str, i: int, key: str, j: int) -> int:
    # base case, input completed
    if j == len(key):
        return 0
    # ...

func dp(ring string, i int, key string, j int) int {
    // base case, input is complete
    if j == len(key) {
        return 0
    }
    // ...
}

var dp = function(ring, i, key, j) {
    // base case, input completed
    if (j === key.length) return 0;
    // ...
};

Next, consider how to make choices based on the state and how to transition between states.

"Choice" refers to "how to move the pointer to obtain the desired input character."

Specifically, for the character key[j] that you want to input, how can the dial be moved to get this character?

For example, if the input is ring = "gdonidg", the state of the dial is shown below:

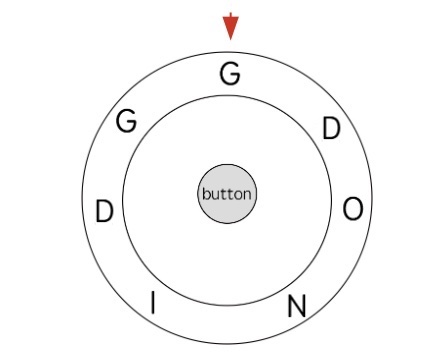
Assume the character you want to input is key[j] = "d". There are two letters "d" on the dial, and you can move the pointer clockwise or counterclockwise. Therefore, there are four "choices" to input the character "d", and we need to choose the method with the least number of operations.

The general code logic is as follows:

int dp(String ring, int i, String key, int j) {
    // base case: finished input
    if (j == key.length()) return 0;
    
    // make a choice
    int res = Integer.MAX_VALUE;
    for (int k : [all indices of character key[j] in ring]) {
        res = min(
            cost of rotating i clockwise to k,
            cost of rotating i counterclockwise to k
        );
    }
    
    return res;
}

As for whether to move clockwise or counterclockwise, it's straightforward to decide; just choose the closer direction. However, for the two characters "d" on the dial, can you still choose the closer one?

No, because it depends on the character that needs to be input after key[i]. Consider the previous example:

If the input is key = "di", even if the right "d" is closer, you should choose the left "d" because the "i" is right next to the left "d", resulting in fewer overall operations.

So, how should it be determined? Essentially, it's brute-force search. Recursively call the dp function to calculate the "overall" cost of both choices, then compare them.

That's about it. Let's look at the final code:

class Solution {
    // character -> index list
    private Map<Character, List<Integer>> charToIndex = new HashMap<>();
    // memoization
    private int[][] memo;

    // main function
    public int findRotateSteps(String ring, String key) {
        int m = ring.length();
        int n = key.length();
        // initialize all memoization entries to 0
        memo = new int[m][n];
        // record the mapping of characters to indices on the ring
        for (int i = 0; i < ring.length(); i++) {
            char c = ring.charAt(i);
            if (!charToIndex.containsKey(c)) {
                charToIndex.put(c, new ArrayList<>());
            }
            charToIndex.get(c).add(i);
        }
        // the initial pointer of the ring points at the 12 o'clock direction,
        // start inputting the key from the first character
        return dp(ring, 0, key, 0);
    }

    // calculate the minimum number of operations when the
    // pointer is at ring[i] and inputting key[j..]
    private int dp(String ring, int i, String key, int j) {
        // base case: finished inputting
        if (j == key.length()) return 0;
        // check the memoization to avoid overlapping subproblems
        if (memo[i][j] != 0) return memo[i][j];

        int n = ring.length();
        // make choices
        int res = Integer.MAX_VALUE;
        // there might be multiple characters key[j] on the ring
        for (int k : charToIndex.get(key.charAt(j))) {
            // number of times to move the pointer
            int delta = Math.abs(k - i);
            // choose clockwise or counterclockwise
            delta = Math.min(delta, n - delta);
            // move the pointer to ring[k] and continue inputting key[j+1..]
            int subProblem = dp(ring, k, key, j + 1);
            // choose the overall minimum number of operations
            // add one because pressing the button is also an operation
            res = Math.min(res, 1 + delta + subProblem);
        }
        // store the result in the memoization table
        memo[i][j] = res;
        return res;
    }
}

#include <unordered_map>
#include <vector>
#include <string>
#include <algorithm>
#include <limits>

using namespace std;

class Solution {
    // character -> index list
    unordered_map<char, vector<int>> charToIndex;
    // memoization
    vector<vector<int>> memo;

    // calculate the minimum number of operations when the
    // pointer is at ring[i] and inputting key[j..]
    int dp(const string& ring, int i, const string& key, int j) {
        // base case: finished inputting
        if (j == key.size()) return 0;
        // check the memoization to avoid overlapping subproblems
        if (memo[i][j] != 0) return memo[i][j];

        int n = ring.size();
        // make choices
        int res = numeric_limits<int>::max();
        // there might be multiple characters key[j] on the ring
        for (int k : charToIndex[key[j]]) {
            // number of times to move the pointer
            int delta = abs(k - i);
            // choose clockwise or counterclockwise
            delta = min(delta, n - delta);
            // move the pointer to ring[k] and continue inputting key[j+1..]
            int subProblem = dp(ring, k, key, j + 1);
            // choose the overall minimum number of operations
            // add one because pressing the button is also an operation
            res = min(res, 1 + delta + subProblem);
        }
        // store the result in the memoization table
        memo[i][j] = res;
        return res;
    }

public:
    // main function
    int findRotateSteps(string ring, string key) {
        int m = ring.size();
        int n = key.size();
        // initialize all memoization entries to 0
        memo = vector<vector<int>>(m, vector<int>(n, 0));
        // record the mapping of characters to indices on the ring
        for (int i = 0; i < ring.size(); i++) {
            char c = ring[i];
            charToIndex[c].push_back(i);
        }
        // the initial pointer of the ring points at the 12 o'clock direction,
        // start inputting the key from the first character
        return dp(ring, 0, key, 0);
    }
};

class Solution:
    # character -> index list
    def __init__(self):
        self.charToIndex = {}
        # memoization
        self.memo = []

    # main function
    def findRotateSteps(self, ring: str, key: str) -> int:
        m = len(ring)
        n = len(key)
        # initialize all memoization entries to 0
        self.memo = [[0] * n for _ in range(m)]
        # record the mapping of characters to indices on the ring
        for i, c in enumerate(ring):
            if c not in self.charToIndex:
                self.charToIndex[c] = []
            self.charToIndex[c].append(i)
        # the initial pointer of the ring points at the 12 o'clock direction,
        # start inputting the key from the first character
        return self.dp(ring, 0, key, 0)

    # calculate the minimum number of operations when
    # the pointer is at ring[i] and inputting key[j..]
    def dp(self, ring: str, i: int, key: str, j: int) -> int:
        # base case: finished inputting
        if j == len(key):
            return 0
        # check the memoization to avoid overlapping subproblems
        if self.memo[i][j] != 0:
            return self.memo[i][j]

        n = len(ring)
        # make choices
        res = float('inf')
        # there might be multiple characters key[j] on the ring
        for k in self.charToIndex[key[j]]:
            # number of times to move the pointer
            delta = abs(k - i)
            # choose clockwise or counterclockwise
            delta = min(delta, n - delta)
            # move the pointer to ring[k] and continue inputting key[j+1..]
            subProblem = self.dp(ring, k, key, j + 1)
            # choose the overall minimum number of operations
            # add one because pressing the button is also an operation
            res = min(res, 1 + delta + subProblem)
        # store the result in the memoization table
        self.memo[i][j] = res
        return res

// main function
func findRotateSteps(ring string, key string) int {
    // character -> index list
    charToIndex := make(map[rune][]int)
    // memoization
    memo := make([][]int, len(ring))
    // initialize all memoization entries to 0
    for i := range memo {
        memo[i] = make([]int, len(key))
    }

    // record the mapping of characters to indices on the ring
    for i, c := range ring {
        charToIndex[c] = append(charToIndex[c], i)
    }

    // the initial pointer of the ring points at the 12 o'clock direction,
    // start inputting the key from the first character
    return dp(ring, 0, key, 0, charToIndex, memo)
}

// calculate the minimum number of operations when
// the pointer is at ring[i] and inputting key[j..]
func dp(ring string, i int, key string, j int, charToIndex map[rune][]int, memo [][]int) int {
    // base case: finished inputting
    if j == len(key) {
        return 0
    }
    // check the memoization to avoid overlapping subproblems
    if memo[i][j] != 0 {
        return memo[i][j]
    }

    n := len(ring)
    // make choices
    res := int(^uint(0) >> 1) // Initialize res to the maximum int value
    // there might be multiple characters key[j] on the ring
    for _, k := range charToIndex[rune(key[j])] {
        // number of times to move the pointer
        delta := abs(k - i)
        // choose clockwise or counterclockwise
        delta = min(delta, n - delta)
        // move the pointer to ring[k] and continue inputting key[j+1..]
        subProblem := dp(ring, k, key, j + 1, charToIndex, memo)
        // choose the overall minimum number of operations
        // add one because pressing the button is also an operation
        res = min(res, 1 + delta + subProblem)
    }
    // store the result in the memoization table
    memo[i][j] = res
    return res
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

func abs(a int) int {
    if a < 0 {
        return -a
    }
    return a
}

var findRotateSteps = function(ring, key) {
    // character -> index list
    let charToIndex = {};
    // memoization
    let memo = [];

    // record the mapping of characters to indices on the ring
    for (let i = 0; i < ring.length; i++) {
        let c = ring[i];
        if (!charToIndex[c]) {
            charToIndex[c] = [];
        }
        charToIndex[c].push(i);
    }

    // initialize all memoization entries to 0
    for (let i = 0; i < ring.length; i++) {
        memo[i] = Array(key.length).fill(0);
    }

    // main function
    // the initial pointer of the ring points at the 12 o'clock direction,
    // start inputting the key from the first character
    return dp(0, 0);

    // calculate the minimum number of operations when the
    // pointer is at ring[i] and inputting key[j..]
    function dp(i, j) {
        // base case: finished inputting
        if (j == key.length) return 0;
        // check the memoization to avoid overlapping subproblems
        if (memo[i][j] != 0) return memo[i][j];

        let n = ring.length;
        // make choices
        let res = Number.MAX_VALUE;
        // there might be multiple characters key[j] on the ring
        for (let k of charToIndex[key[j]]) {
            // number of times to move the pointer
            let delta = Math.abs(k - i);
            // choose clockwise or counterclockwise
            delta = Math.min(delta, n - delta);
            // move the pointer to ring[k] and continue inputting key[j+1..]
            let subProblem = dp(k, j + 1);
            // choose the overall minimum number of operations
            // add one because pressing the button is also an operation
            res = Math.min(res, 1 + delta + subProblem);
        }
        // store the result in the memoization table
        memo[i][j] = res;
        return res;
    }
};