Classic DP: Edit Distance

A few days ago, I saw an interview question from Tencent. Most of the algorithm section was about dynamic programming, and the last question was to write a function to calculate the edit distance. Today, I will write a dedicated article to discuss this problem.

LeetCode Problem 72 "Edit Distance" is exactly about this topic. Let's look at the problem first:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

// The function signature is as follows
int minDistance(String s1, String s2)

// The function signature is as follows
int minDistance(string s1, string s2)

# The function signature is as follows
def minDistance(s1: str, s2: str) -> int:

// the function signature is as follows
func minDistance(s1 string, s2 string) int {}

// The function signature is as follows
var minDistance = function(s1, s2) {}

For readers who have not encountered dynamic programming problems before, this question can be quite challenging. Does it feel like you don't know where to begin?

However, this problem is actually very practical. I have used this algorithm in real life. In the past, I wrote a public article and accidentally misplaced a section of content. I decided to fix this part to make the logic clear. But the platform only allows you to edit up to 20 characters, supporting only insert, delete, and replace operations (exactly like the edit distance problem). So, I used the algorithm to find the optimal solution and completed the modification in just 16 steps.

Another more advanced application is in DNA sequences, which are composed of A, G, C, T and can be viewed as strings. Edit distance can measure the similarity between two DNA sequences. The smaller the edit distance, the more similar the two DNA strands are. It's possible that the owners of those DNAs are ancient relatives.

Now, let's get back to the main topic and explain in detail how to calculate the edit distance. I believe this article will be helpful to you.

1. Approach

The edit distance problem involves transforming one string s1 into another string s2 using three types of operations, and finding the minimum number of such operations. It's important to note that transforming s1 to s2 is equivalent to transforming s2 to s1, so we will use the former as an example.

Suppose the two strings are "rad" and "apple", and the pointers i and j point to the tails of s1 and s2, respectively. To transform s1 into s2, the algorithm proceeds as follows:

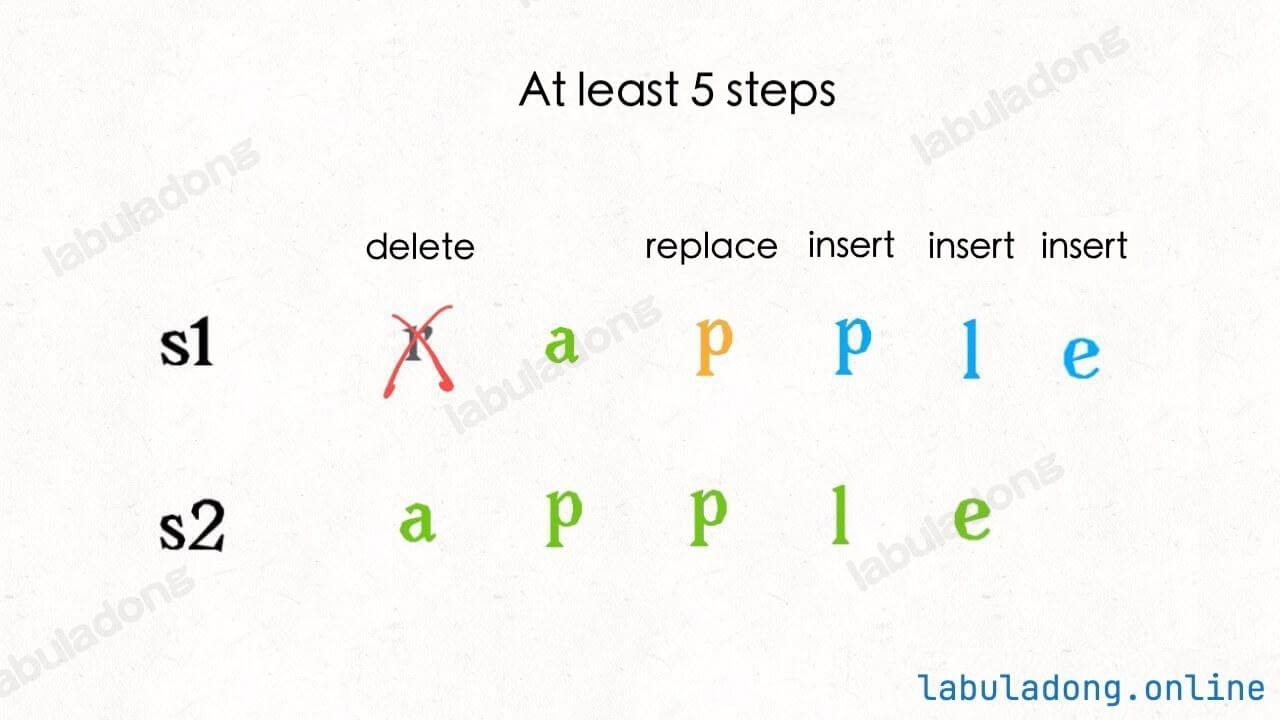
Remember this GIF process, as it will help you calculate the edit distance. The key is to perform the correct operations, which will be explained shortly.

From the GIF above, you can see that there is actually a fourth operation: do nothing (skip). For example, in this situation:

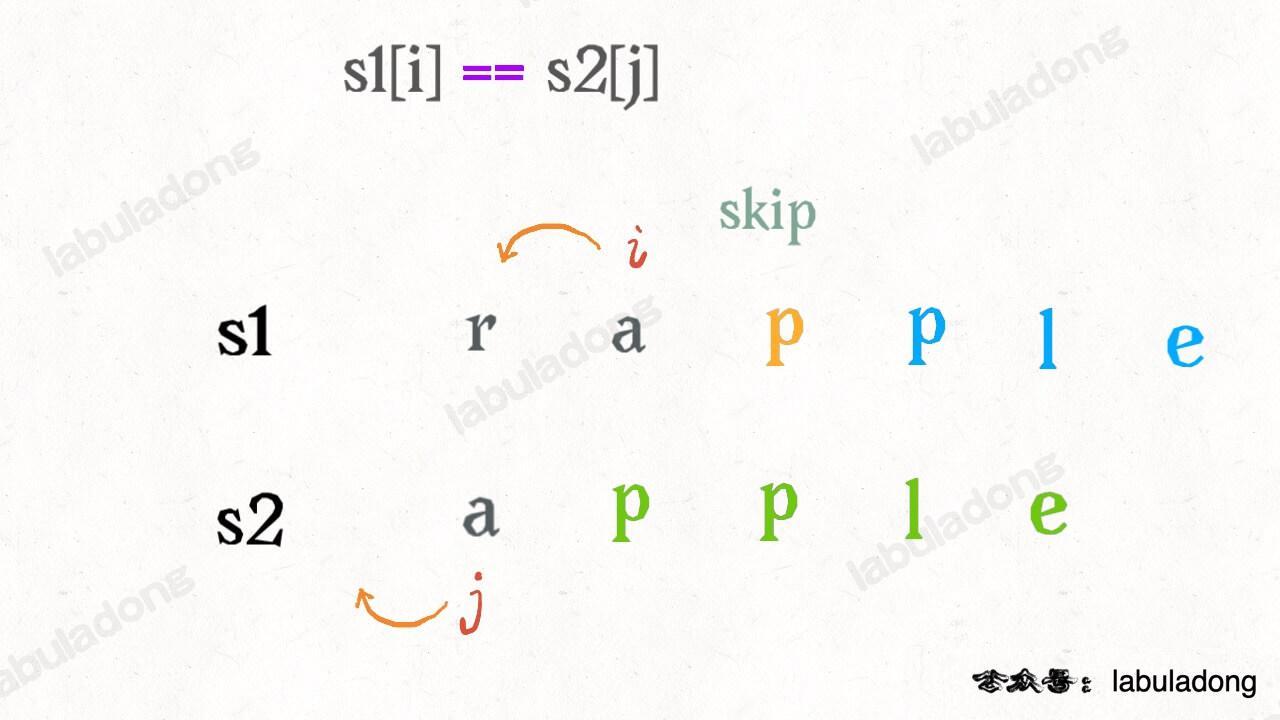
Since these two characters are already the same, to minimize the edit distance, obviously no operation should be performed. Simply move i and j forward.

Another easy-to-handle situation is when j reaches the end of s2 but i has not reached the end of s1. In this case, you can only use the delete operation to shorten s1 to match s2. For example:

Similarly, if i reaches the end of s1 while j has not reached the end of s2, you can only use the insert operation to add all the remaining characters of s2 to s1. These two situations are the base cases of the algorithm.

Next, let's detail how to translate this approach into code.

2. Detailed Code Explanation

Let's first review the previous approach:

The base case occurs when i traverses through s1 or j through s2, at which point you can directly return the remaining length of the other string.

For each pair of characters s1[i] and s2[j], there are four possible operations:

if s1[i] == s2[j]:
    Do nothing (skip)
    Move both i and j forward
else:
    Choose one of three:
        Insert
        Delete
        Replace

With this framework, the problem is essentially solved. Readers might ask, how exactly should we choose among the "three options"? It's simple: try all of them, and choose the one that results in the minimum edit distance. Here, recursion is necessary. Let's first look at the brute-force solution code:

class Solution {
    public int minDistance(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        // i, j are initialized to point to the last index
        return dp(s1, m - 1, s2, n - 1);
    }

    // definition: return the minimum edit distance between s1[0..i] and s2[0..j]
    int dp(String s1, int i, String s2, int j) {
        // base case
        if (i == -1) return j + 1;
        if (j == -1) return i + 1;

        if (s1.charAt(i) == s2.charAt(j)) {
            // do nothing
            return dp(s1, i - 1, s2, j - 1);
        }
        return min(
            // insert
            dp(s1, i, s2, j - 1) + 1,
            // delete
            dp(s1, i - 1, s2, j) + 1,
            // replace
            dp(s1, i - 1, s2, j - 1) + 1
        );
    }

    int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}

class Solution {
public:
    int minDistance(string s1, string s2) {
        int m = s1.size(), n = s2.size();
        // initialize i and j to point to the last index
        return dp(s1, m - 1, s2, n - 1);
    }

private:
    // definition: return the minimum edit distance between s1[0..i] and s2[0..j]
    int dp(string &s1, int i, string &s2, int j) {
        // base case
        if (i == -1) return j + 1;
        if (j == -1) return i + 1;

        if (s1[i] == s2[j]) {
            // do nothing
            return dp(s1, i - 1, s2, j - 1);
        }
        return min({
            // insert
            dp(s1, i, s2, j - 1) + 1,
            // delete
            dp(s1, i - 1, s2, j) + 1,
            // replace
            dp(s1, i - 1, s2, j - 1) + 1
        });
    }
};

class Solution:
    def minDistance(self, s1: str, s2: str) -> int:
        m = len(s1)
        n = len(s2)
        # initialize i and j to point to the last index
        return self.dp(s1, m - 1, s2, n - 1)

    # definition: return the minimum edit distance between s1[0..i] and s2[0..j]
    def dp(self, s1: str, i: int, s2: str, j: int) -> int:
        # base case
        if i == -1:
            return j + 1
        if j == -1:
            return i + 1

        if s1[i] == s2[j]:
            # do nothing
            return self.dp(s1, i - 1, s2, j - 1)

        return min(
            # insert
            self.dp(s1, i, s2, j - 1) + 1,
            # delete
            self.dp(s1, i - 1, s2, j) + 1,
            # replace
            self.dp(s1, i - 1, s2, j - 1) + 1
        )

func minDistance(s1 string, s2 string) int {
    m, n := len(s1), len(s2)
    // initialize i and j to point to the last index
    return dp(s1, m - 1, s2, n - 1)
}

// definition: return the minimum edit distance between s1[0..i] and s2[0..j]
func dp(s1 string, i int, s2 string, j int) int {
    // base case
    if i == -1 {
        return j + 1
    }
    if j == -1 {
        return i + 1
    }

    if s1[i] == s2[j] {
        // do nothing
        return dp(s1, i - 1, s2, j - 1)
    }
    return min(
        // insert
        dp(s1, i, s2, j - 1) + 1,
        // delete
        dp(s1, i - 1, s2, j) + 1,
        // replace
        dp(s1, i - 1, s2, j - 1) + 1
    )
}

var minDistance = function(s1, s2) {
    let m = s1.length, n = s2.length;
    // initialize i and j to point to the last index
    return dp(s1, m - 1, s2, n - 1);
}

// definition: return the minimum edit distance between s1[0..i] and s2[0..j]
var dp = function(s1, i, s2, j) {
    // base case
    if (i == -1) return j + 1;
    if (j == -1) return i + 1;

    if (s1.charAt(i) == s2.charAt(j)) {
        // do nothing
        return dp(s1, i - 1, s2, j - 1);
    }
    return min(
        // insert
        dp(s1, i, s2, j - 1) + 1,
        // delete
        dp(s1, i - 1, s2, j) + 1,
        // replace
        dp(s1, i - 1, s2, j - 1) + 1,
    );
}

var min = function(a, b, c) {
    return Math.min(a, Math.min(b, c));
}

Now, let's explain this recursive code in detail. The base case should be self-explanatory, so let's focus on the recursive part.

It's often said that recursive code is highly interpretable, and there is a reason for that. As long as you understand the function's definition, you can clearly understand the algorithm's logic. Here, the dp function is defined as follows:

// Definition: return the minimum edit distance between s1[0..i] and s2[0..j]
int dp(String s1, int i, String s2, int j)

// Definition: return the minimum edit distance between s1[0..i] and s2[0..j]
int dp(string s1, int i, string s2, int j)

# Definition: Return the minimum edit distance between s1[0..i] and s2[0..j]
def dp(s1: str, i: int, s2: str, j: int):

// Definition: return the minimum edit distance between s1[0..i] and s2[0..j]
func dp(s1 string, i int, s2 string, j int) int

// Definition: return the minimum edit distance between s1[0..i] and s2[0..j]
var dp = function(s1, i, s2, j)

Remember this definition, then let's look at this code:

if s1[i] == s2[j]:
    # Do nothing
    return dp(s1, i - 1, s2, j - 1)
# Explanation:
# They are already equal, no operation needed
# The minimum edit distance between s1[0..i] and s2[0..j] equals
# the minimum edit distance between s1[0..i-1] and s2[0..j-1]
# In other words, dp(i, j) equals dp(i-1, j-1)

If s1[i] != s2[j], three operations need to be considered recursively, requiring some thought:

# Insert
dp(s1, i, s2, j - 1) + 1,
# Explanation:
# Insert a character identical to s2[j] after s1[i]
# This matches s2[j], move j forward, continue comparing with i
# Don't forget to add one to the operation count

# Delete
dp(s1, i - 1, s2, j) + 1,
# Explanation:
# Delete the character s[i]
# The minimum edit distance between s1[0..i-1] and s2[0..j] equals
# Move i forward, continue comparing with j
# Add one to the operation count

# Replace
dp(s1, i - 1, s2, j - 1) + 1
# Explanation:
# Replace s1[i] with s2[j], making them match
# Move both i and j forward, continue comparison
# Add one to the operation count

Now, you should fully understand this concise code. A minor issue is that this solution is a brute-force method, with overlapping subproblems that require dynamic programming techniques for optimization.

How to identify overlapping subproblems at a glance? I have discussed this in Dynamic Programming Q&A. To briefly mention, it is necessary to abstract the recursive framework of this algorithm:

int dp(i, j) {
    dp(i - 1, j - 1); // #1
    dp(i, j - 1);     // #2
    dp(i - 1, j);     // #3
}

For the subproblem dp(i-1, j-1), how can it be derived from the original problem dp(i, j)? There is more than one path, such as dp(i, j) -> #1 and dp(i, j) -> #2 -> #3. Once a duplicate path is found, it indicates a significant number of duplicate paths, meaning overlapping subproblems exist.

3. Dynamic Programming Optimization

Regarding overlapping subproblems, as detailed in the previous article Dynamic Programming Detailed Explanation, optimization methods include adding a memoization to the recursive solution or using a DP table to implement the dynamic programming process iteratively. Let's discuss each method.

Memoization Solution

Since the brute-force recursive solution is already written, adding memoization is straightforward, with slight modifications to the original code:

class Solution {
    // memoization
    int[][] memo;
        
    public int minDistance(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        // initialize the memoization with a special value,
        // indicating it has not been calculated
        memo = new int[m][n];
        for (int[] row : memo) {
            Arrays.fill(row, -1);
        }
        return dp(s1, m - 1, s2, n - 1);
    }

    int dp(String s1, int i, String s2, int j) {
        if (i == -1) return j + 1;
        if (j == -1) return i + 1;
        // check the memoization to avoid overlapping subproblems
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // state transition, store the result in memoization
        if (s1.charAt(i) == s2.charAt(j)) {
            memo[i][j] = dp(s1, i - 1, s2, j - 1);
        } else {
            memo[i][j] =  min(
                dp(s1, i, s2, j - 1) + 1,
                dp(s1, i - 1, s2, j) + 1,
                dp(s1, i - 1, s2, j - 1) + 1
            );
        }
        return memo[i][j];
    }

    int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}

class Solution {
private:
    // memoization table
    vector<vector<int>> memo;
    int dp(string& s1, int i, string& s2, int j) {
        if (i == -1) return j + 1;
        if (j == -1) return i + 1;
        // check memoization table to avoid overlapping subproblems
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // state transition, store the result in the memoization table
        if (s1[i] == s2[j]) {
            memo[i][j] = dp(s1, i - 1, s2, j - 1);
        } else {
            memo[i][j] = min3(
                dp(s1, i, s2, j - 1) + 1,
                dp(s1, i - 1, s2, j) + 1,
                dp(s1, i - 1, s2, j - 1) + 1
            );
        }
        return memo[i][j];
    }

    int min3(int a, int b, int c) {
        return min(a, min(b, c));
    }

public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        // initialize the memoization table with a special
        // value, indicating it has not been calculated
        memo = vector<vector<int>>(m, vector<int>(n, -1));
        return dp(word1, m - 1, word2, n - 1);
    }
};

class Solution:
    def __init__(self):
        self.memo = []

    def minDistance(self, s1: str, s2: str) -> int:
        m, n = len(s1), len(s2)
        # Initialize the memoization table with a special value,
        # indicating that it has not been calculated yet
        self.memo = [[-1] * n for _ in range(m)]
        return self.dp(s1, m - 1, s2, n - 1)

    def dp(self, s1: str, i: int, s2: str, j: int) -> int:
        if i == -1:
            return j + 1
        if j == -1:
            return i + 1

        # Check the memoization table to avoid overlapping subproblems
        if self.memo[i][j] != -1:
            return self.memo[i][j]

        # State transition, store the result in the memoization table
        if s1[i] == s2[j]:
            self.memo[i][j] = self.dp(s1, i - 1, s2, j - 1)
        else:
            self.memo[i][j] = min(
                self.dp(s1, i, s2, j - 1) + 1,
                self.dp(s1, i - 1, s2, j) + 1,
                self.dp(s1, i - 1, s2, j - 1) + 1
            )

        return self.memo[i][j]

func minDistance(s1 string, s2 string) int {
    // memoization table
    memo := make([][]int, len(s1))
    for i := range memo {
        memo[i] = make([]int, len(s2))
        for j := range memo[i] {
            memo[i][j] = -1
        }
    }
    return dp(s1, len(s1)-1, s2, len(s2)-1, memo)
}

func dp(s1 string, i int, s2 string, j int, memo [][]int) int {
    if i == -1 {
        return j + 1
    }
    if j == -1 {
        return i + 1
    }
    // check the memoization table to avoid overlapping subproblems
    if memo[i][j] != -1 {
        return memo[i][j]
    }
    // state transition, store the result in the memoization table
    if s1[i] == s2[j] {
        memo[i][j] = dp(s1, i-1, s2, j-1, memo)
    } else {
        memo[i][j] = min(
            dp(s1, i, s2, j-1, memo)+1,
            dp(s1, i-1, s2, j, memo)+1,
            dp(s1, i-1, s2, j-1, memo)+1,
        )
    }
    return memo[i][j]
}

func min(a int, b int, c int) int {
    if a < b {
        if a < c {
            return a
        }
        return c
    }
    if b < c {
        return b
    }
    return c
}

var minDistance = function(s1, s2) {
    let memo = [];
    let m = s1.length, n = s2.length;
    // Initialize the memoization array with a special
    // value, indicating that it has not been calculated yet
    for (let i = 0; i <= m; i++) {
        memo[i] = new Array(n + 1).fill(-1);
    }
    return dp(s1, m - 1, s2, n - 1, memo);
};

function dp(s1, i, s2, j, memo) {
    if (i == -1) return j + 1;
    if (j == -1) return i + 1;
    // Check the memoization array to avoid overlapping subproblems
    if (memo[i][j] != -1) {
        return memo[i][j];
    }
    // State transition, store the result in the memoization array
    if (s1.charAt(i) == s2.charAt(j)) {
        memo[i][j] = dp(s1, i - 1, s2, j - 1, memo);
    } else {
        memo[i][j] = Math.min(
            dp(s1, i, s2, j - 1, memo) + 1,
            dp(s1, i - 1, s2, j, memo) + 1,
            dp(s1, i - 1, s2, j - 1, memo) + 1
        );
    }
    return memo[i][j];
}

DP Table Solution

Let's discuss the DP table solution. We need to define a dp array and apply the state transition equation on this array.

First, clarify the meaning of the dp array. Since this problem involves two states (indices i and j), the dp array is a two-dimensional array, structured as follows:

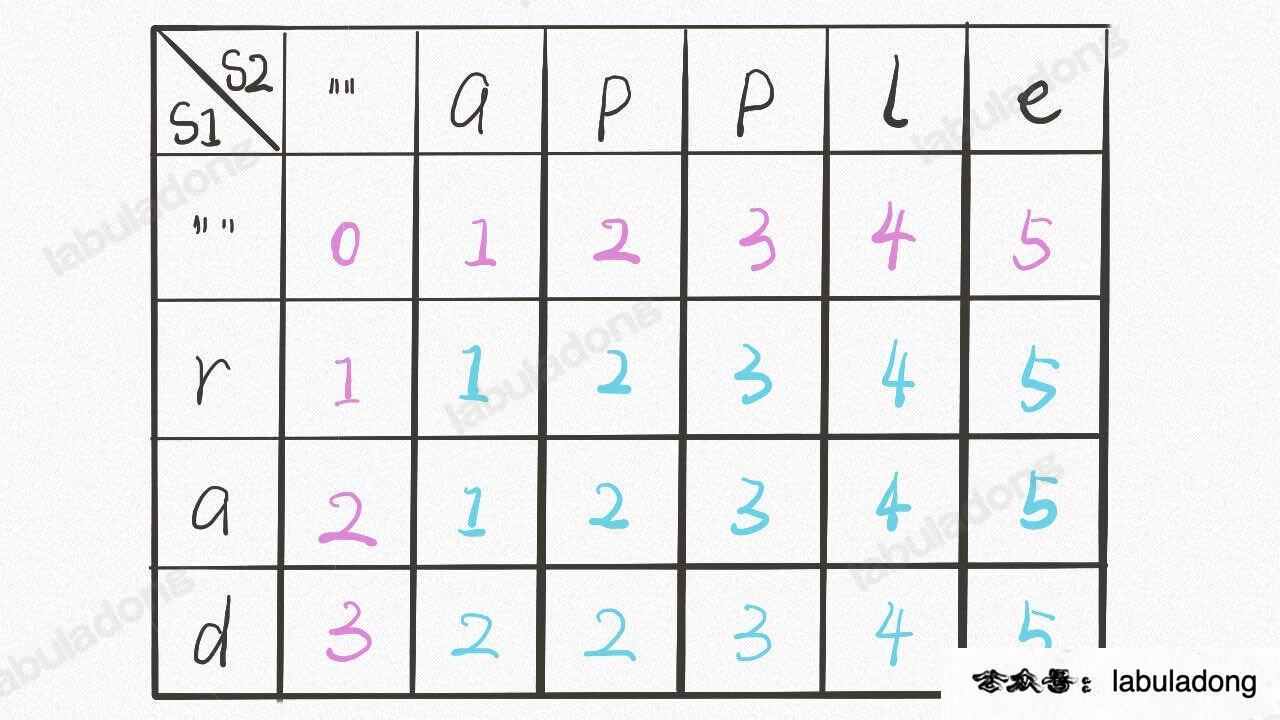
The state transition is the same as in the recursive solution. dp[..][0] and dp[0][..] correspond to the base case, and the meaning of dp[i][j] is similar to the previous definition of the dp function:

int dp(String s1, int i, String s2, int j)
// Returns the minimum edit distance between s1[0..i] and s2[0..j]

dp[i-1][j-1]
// Stores the minimum edit distance between s1[0..i] and s2[0..j]

The base case for the dp function is when i, j equals -1, but array indices start at least from 0, so the dp array is offset by one position.

Since the dp array and the recursive dp function share the same meaning, you can directly apply the previous approach in writing the code. The only difference is that the recursive solution solves from top to bottom (starting from the original problem and breaking it down to the base case), whereas the DP table solves from bottom to top (starting from the base case and building up to the original problem):

class Solution {
    public int minDistance(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        int[][] dp = new int[m + 1][n + 1];
        // base case
        for (int i = 1; i <= m; i++)
            dp[i][0] = i;
        for (int j = 1; j <= n; j++)
            dp[0][j] = j;
        // bottom-up calculation
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                if (s1.charAt(i - 1) == s2.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = min(
                        dp[i - 1][j] + 1,

                        dp[i][j - 1] + 1,

                        dp[i - 1][j - 1] + 1

                    );
        // stores the minimum edit distance between s1 and s2
        return dp[m][n];
    }

    int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}

class Solution {
public:
    int minDistance(string s1, string s2) {
        int m = s1.length(), n = s2.length();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        // base case
        for (int i = 1; i <= m; i++)
            dp[i][0] = i;
        for (int j = 1; j <= n; j++)
            dp[0][j] = j;
        // bottom-up calculation
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s1[i - 1] == s2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = min(
                        dp[i - 1][j] + 1,

                        dp[i][j - 1] + 1,

                        dp[i - 1][j - 1] + 1

                    );
            }
        }
        // stores the minimum edit distance between s1 and s2
        return dp[m][n];
    }

    int min(int a, int b, int c) {
        return std::min(a, std::min(b, c));
    }
};

class Solution:
    def minDistance(self, s1: str, s2: str) -> int:
        m, n = len(s1), len(s2)
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        # base case
        for i in range(1, m + 1):
            dp[i][0] = i
        for j in range(1, n + 1):
            dp[0][j] = j
        # bottom-up calculation
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if s1[i - 1] == s2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = min(
                        dp[i - 1][j] + 1,
                        # <extend up -300>
                        # <div class="img-content"><img src="/images/editDistance/delete.gif" alt class="myimage" loading="lazy" photo-swipe="" /></div>
                        dp[i][j - 1] + 1,
                        # <extend up -300>
                        # <div class="img-content"><img src="/images/editDistance/insert.gif" alt class="myimage" loading="lazy" photo-swipe="" /></div>
                        dp[i - 1][j - 1] + 1
                        # <extend up -300>
                        # <div class="img-content"><img src="/images/editDistance/replace.gif" alt class="myimage" loading="lazy" photo-swipe="" /></div>
                    )
        # stores the minimum edit distance between s1 and s2
        return dp[m][n]

    def min(self, a: int, b: int, c: int) -> int:
        return min(a, min(b, c))

func minDistance(s1 string, s2 string) int {
    m, n := len(s1), len(s2)
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
    }
    // base case
    for i := 1; i <= m; i++ {
        dp[i][0] = i
    }
    for j := 1; j <= n; j++ {
        dp[0][j] = j
    }
    // bottom-up calculation
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            if s1[i-1] == s2[j-1] {
                dp[i][j] = dp[i-1][j-1]
            } else {
                dp[i][j] = min(
                    dp[i-1][j]+1,
                    dp[i][j-1]+1,
                    dp[i-1][j-1]+1,
                )
            }
        }
    }
    // stores the minimum edit distance between s1 and s2
    return dp[m][n]
}

func min(a, b, c int) int {
    if a < b {
        if a < c {
            return a
        }
        return c
    }
    if b < c {
        return b
    }
    return c
}

var minDistance = function(s1, s2) {
    let m = s1.length, n = s2.length;
    let dp = Array.from({length: m + 1}, () => Array(n + 1).fill(0));
    
    // base case
    for (let i = 1; i <= m; i++)
        dp[i][0] = i;
    for (let j = 1; j <= n; j++)
        dp[0][j] = j;
    
    // bottom-up calculation
    for (let i = 1; i <= m; i++)
        for (let j = 1; j <= n; j++)
            if (s1.charAt(i - 1) === s2.charAt(j - 1))
                dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] = Math.min(
                    dp[i - 1][j] + 1,
                    dp[i][j - 1] + 1,
                    dp[i - 1][j - 1] + 1
                );

    // stores the minimum edit distance between s1 and s2
    return dp[m][n];
};

IV. Further Exploration

Generally, when dealing with dynamic programming problems involving two strings, the approach outlined in this article is used to establish a DP table. Why? Because it's easier to identify the state transitions, for example, the DP table for edit distance:

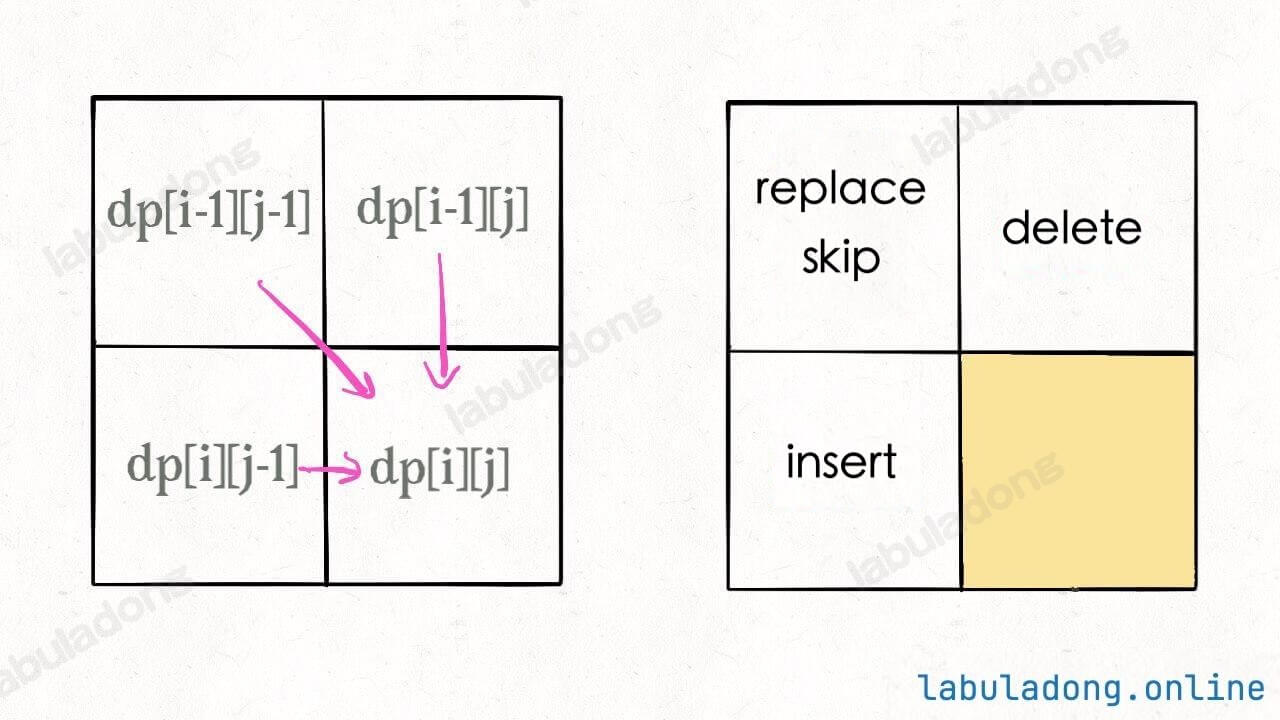
There's another detail: since each dp[i][j] is only related to the three nearby states, the space complexity can be reduced to $O(min(M, N))$ (where M and N are the lengths of the two strings). This is not difficult, but it greatly reduces interpretability, so readers can try optimizing it themselves.

You might also ask, this only finds the minimum edit distance, but what are the specific operations? In the example of modifying a WeChat public account article you gave, just knowing the minimum edit distance is not enough; you also need to know the specific modifications.

This is actually quite simple. With slight modifications to the code, additional information can be added to the dp array:

// int[][] dp;
Node[][] dp;

class Node {
    int val;
    int choice;
    // 0 represents doing nothing
    // 1 represents insertion
    // 2 represents deletion
    // 3 represents replacement
}

class Node {
public:
    int val;
    int choice;
    // 0 represents doing nothing
    // 1 represents insertion
    // 2 represents deletion
    // 3 represents replacement
};

vector<vector<Node>> dp;

class Node:
    val: int
    choice: int
    # 0 represents doing nothing
    # 1 represents insertion
    # 2 represents deletion
    # 3 represents replacement

dp: List[List[Node]] = []

// Node struct
type Node struct {
    val    int
    choice int
    // 0 means do nothing
    // 1 means insert
    // 2 means delete
    // 3 means replace
}

var dp [][]Node

class Node {
    constructor(val, choice) {
        this.val = val;
        this.choice = choice;
    }
}

const dp: Node[][] = [];

The val attribute represents the previous value of the dp array, and the choice attribute represents the operation. When making the optimal choice, record the operation at the same time, and then backtrack from the result to get the specific operations.

Our final result is dp[m][n], where val stores the minimum edit distance and choice stores the last operation, for example, an insertion operation, allowing you to move left one step:

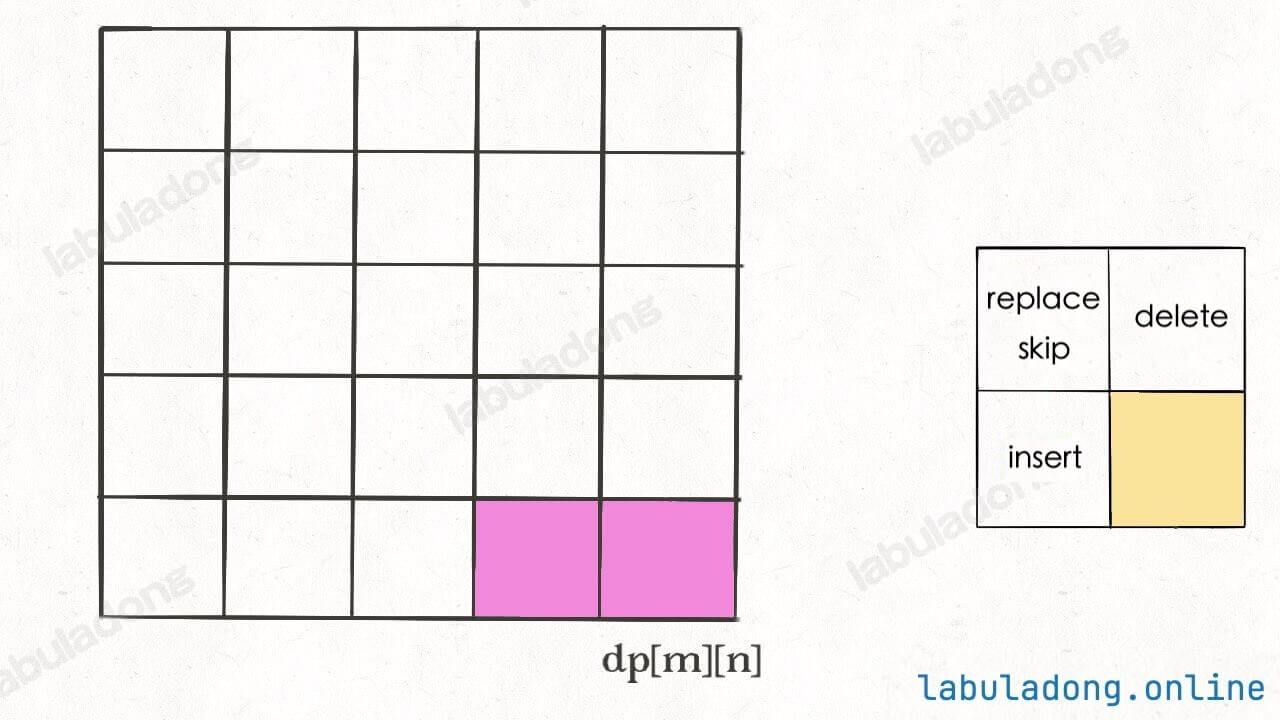
By repeating this process, you can step back to the starting point dp[0][0], forming a path. Following the operations on this path for editing provides the optimal solution.

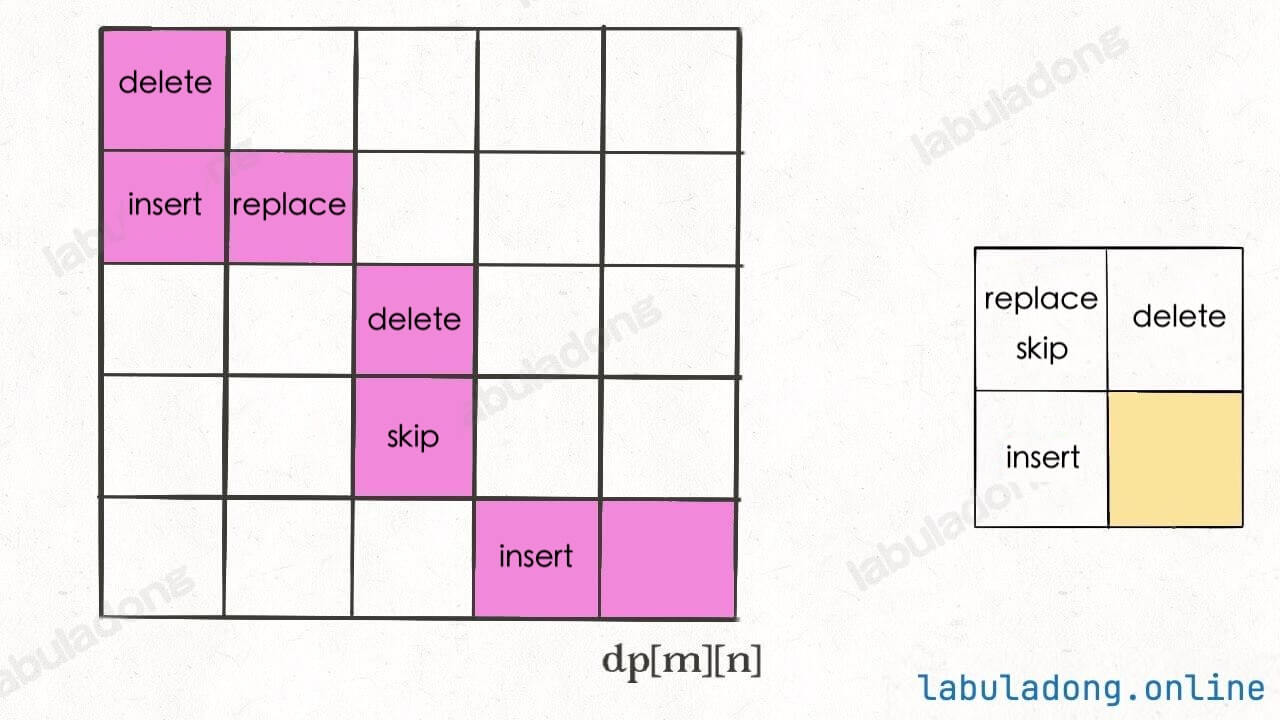
At everyone's request, I have written this approach as well, and you can try running it yourself:

int minDistance(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    Node[][] dp = new Node[m + 1][n + 1];
    // base case
    for (int i = 0; i <= m; i++) {
        // transforming s1 to s2 only requires deleting a character
        dp[i][0] = new Node(i, 2);
    }
    for (int j = 1; j <= n; j++) {
        // transforming s1 to s2 only requires inserting a character
        dp[0][j] = new Node(j, 1);
    }
    // state transition equation
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (s1.charAt(i-1) == s2.charAt(j-1)){
                // if the two characters are the same, nothing needs to be done
                Node node = dp[i - 1][j - 1];
                dp[i][j] = new Node(node.val, 0);
            } else {
                // otherwise, record the operation with the minimum cost
                dp[i][j] = minNode(
                    dp[i - 1][j],
                    dp[i][j - 1],
                    dp[i-1][j-1]
                );
                // and increment the edit distance by one
                dp[i][j].val++;
            }
        }
    }
    // deduce the specific operation process based on the dp table and print it
    printResult(dp, s1, s2);
    return dp[m][n].val;
}

// calculate the operation with the minimum cost among delete, insert, replace
Node minNode(Node a, Node b, Node c) {
    Node res = new Node(a.val, 2);
    
    if (res.val > b.val) {
        res.val = b.val;
        res.choice = 1;
    }
    if (res.val > c.val) {
        res.val = c.val;
        res.choice = 3;
    }
    return res;
}


// deduce the result and print the specific operations
void printResult(Node[][] dp, String s1, String s2) {
    int rows = dp.length;
    int cols = dp[0].length;
    int i = rows - 1, j = cols - 1;
    System.out.println("Change s1=" + s1 + " to s2=" + s2 + ":\n");
    while (i != 0 && j != 0) {
        char c1 = s1.charAt(i - 1);
        char c2 = s2.charAt(j - 1);
        int choice = dp[i][j].choice;
        System.out.print("s1[" + (i - 1) + "]:");
        switch (choice) {
            case 0:
                // skip, then both pointers move forward
                System.out.println("skip '" + c1 + "'");
                i--; j--;
                break;
            case 1:
                // insert s2[j] into s1[i], then the s2 pointer moves forward
                System.out.println("insert '" + c2 + "'");
                j--;
                break;
            case 2:
                // delete s1[i], then the s1 pointer moves forward
                System.out.println("delete '" + c1 + "'");
                i--;
                break;
            case 3:
                // replace s1[i] with s2[j], then both pointers move forward
                System.out.println(
                    "replace '" + c1 + "'" + " with '" + c2 + "'");
                i--; j--;
                break;
        }
    }
    // if s1 is not finished, the remaining characters need to be deleted
    while (i > 0) {
        System.out.print("s1[" + (i - 1) + "]:");
        System.out.println("delete '" + s1.charAt(i - 1) + "'");
        i--;
    }
    // if s2 is not finished, the remaining characters need to be inserted into s1
    while (j > 0) {
        System.out.print("s1[0]:");
        System.out.println("insert '" + s2.charAt(j - 1) + "'");
        j--;
    }
}

int minDistance(string s1, string s2) {
    int m = s1.size(), n = s2.size();
    vector<vector<Node>> dp(m + 1, vector<Node>(n + 1));
    // base case
    for (int i = 0; i <= m; i++) {
        // converting s1 to s2 requires only deleting one character
        dp[i][0] = Node{i, 2};
    }
    for (int j = 1; j <= n; j++) {
        // converting s1 to s2 requires only inserting one character
        dp[0][j] = Node{j, 1};
    }
    // state transition equation
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (s1[i-1] == s2[j-1]){
                // if the two characters are the same, nothing needs to be done
                Node node = dp[i - 1][j - 1];
                dp[i][j] = Node{node.val, 0};
            } else {
                // otherwise, record the operation with the minimum cost
                dp[i][j] = minNode(
                    dp[i - 1][j],
                    dp[i][j - 1],
                    dp[i-1][j-1]
                );
                // and increment the edit distance by one
                dp[i][j].val++;
            }
        }
    }
    // deduce the specific operation process based on the dp table and print it
    printResult(dp, s1, s2);
    return dp[m][n].val;
}

// calculate the operation with the minimum cost among delete, insert, replace
Node minNode(Node a, Node b, Node c) {
    Node res = a;
    if (res.val > b.val) {
        res = b;
        res.choice = 1;
    }
    if (res.val > c.val) {
        res = c;
        res.choice = 3;
    }
    return res;
}

// deduce the result and print the specific operations
void printResult(vector<vector<Node>>& dp, string s1, string s2) {
    int rows = dp.size();
    int cols = dp[0].size();
    int i = rows - 1, j = cols - 1;
    cout << "Change s1=" << s1 << " to s2=" << s2 << ":\n" << endl;
    while (i != 0 && j != 0) {
        char c1 = s1[i - 1];
        char c2 = s2[j - 1];
        int choice = dp[i][j].choice;
        cout << "s1[" << i - 1 << "]:";
        switch (choice) {
            case 0:
                // skip, then both pointers move forward
                cout << "skip '" << c1 << "'" << endl;
                i--; j--;
                break;
            case 1:
                // insert s2[j] into s1[i], then the s2 pointer moves forward
                cout << "insert '" << c2 << "'" << endl;
                j--;
                break;
            case 2:
                // delete s1[i], then the s1 pointer moves forward
                cout << "delete '" << c1 << "'" << endl;
                i--;
                break;
            case 3:
                // replace s1[i] with s2[j], then both pointers move forward
                cout << "replace '" << c1 << "' with '" << c2 << "'" << endl;
                i--; j--;
                break;
        }
    }
    // if s1 is not finished, the remaining characters need to be deleted
    while (i > 0) {
        cout << "s1[" << i - 1 << "]:";
        cout << "delete '" << s1[i - 1] << "'" << endl;
        i--;
    }
    // if s2 is not finished, the remaining characters need to be inserted into s1
    while (j > 0) {
        cout << "s1[0]:";
        cout << "insert '" << s2[j - 1] << "'" << endl;
        j--;
    }
}

def minDistance(self, s1: str, s2: str) -> int:
    m, n = len(s1), len(s2)
    dp = [[Node() for _ in range(n + 1)] for _ in range(m + 1)]
    # base case
    for i in range(m + 1):
        # converting s1 to s2 requires only deleting one character
        dp[i][0] = Node(i, 2)
    for j in range(1, n + 1):
        # converting s1 to s2 requires only inserting one character
        dp[0][j] = Node(j, 1)
    # state transition equation
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if s1[i-1] == s2[j-1]:
                # if the two characters are the same, nothing needs to be done
                node = dp[i - 1][j - 1]
                dp[i][j] = Node(node.val, 0)
            else:
                # otherwise, record the operation with the minimum cost
                dp[i][j] = self.minNode(
                    dp[i - 1][j],
                    dp[i][j - 1],
                    dp[i-1][j-1]
                )
                # and increment the edit distance by one
                dp[i][j].val += 1
    # deduce the specific operation process based on the dp table and print it
    self.printResult(dp, s1, s2)
    return dp[m][n].val

# calculate the operation with the minimum cost among delete, insert, replace
def minNode(self, a: Node, b: Node, c: Node) -> Node:
    res = a
    if res.val > b.val:
        res = b
        res.choice = 1
    if res.val > c.val:
        res = c
        res.choice = 3
    return res

# deduce the result and print the specific operations
def printResult(self, dp, s1, s2):
    rows = len(dp)
    cols = len(dp[0])
    i, j = rows - 1, cols - 1
    print(f"Change s1={s1} to s2={s2}:\n")
    while i != 0 and j != 0:
        c1 = s1[i - 1]
        c2 = s2[j - 1]
        choice = dp[i][j].choice
        print(f"s1[{i - 1}]:", end='')
        if choice == 0:
            # skip, then both pointers move forward
            print(f"skip '{c1}'")
            i -= 1
            j -= 1
        elif choice == 1:
            # insert s2[j] into s1[i], then the s2 pointer moves forward
            print(f"insert '{c2}'")
            j -= 1
        elif choice == 2:
            # delete s1[i], then the s1 pointer moves forward
            print(f"delete '{c1}'")
            i -= 1
        elif choice == 3:
            # replace s1[i] with s2[j], then both pointers move forward
            print(f"replace '{c1}' with '{c2}'")
            i -= 1
            j -= 1
    # if s1 is not finished, the remaining characters need to be deleted
    while i > 0:
        print(f"s1[{i - 1}]:", end='')
        print(f"delete '{s1[i - 1]}'")
        i -= 1
    # if s2 is not finished, the remaining characters need to be inserted into s1
    while j > 0:
        print(f"s1[0]:", end='')
        print(f"insert '{s2[j - 1]}'")
        j -= 1

func minDistance(s1 string, s2 string) int {
    m, n := len(s1), len(s2)
    dp := make([][]Node, m+1)
    for i := range dp {
        dp[i] = make([]Node, n+1)
    }
    // base case
    for i := 0; i <= m; i++ {
        // converting s1 to s2 requires only deleting one character
        dp[i][0] = Node{val: i, choice: 2}
    }
    for j := 1; j <= n; j++ {
        // converting s1 to s2 requires only inserting one character
        dp[0][j] = Node{val: j, choice: 1}
    }
    // state transition equation
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            if s1[i-1] == s2[j-1] {
                // if the two characters are the same, nothing needs to be done
                node := dp[i-1][j-1]
                dp[i][j] = Node{val: node.val, choice: 0}
            } else {
                // otherwise, record the operation with the smallest cost
                dp[i][j] = minNode(
                    dp[i-1][j],
                    dp[i][j-1],
                    dp[i-1][j-1],
                )
                // and increment the edit distance by one
                dp[i][j].val++
            }
        }
    }
    // deduce the specific operation process based on the dp table and print it
    printResult(dp, s1, s2)
    return dp[m][n].val
}

// calculate the operation with the smallest cost among delete, insert, replace
func minNode(a, b, c Node) Node {
    res := a
    if res.val > b.val {
        res = b
        res.choice = 1
    }
    if res.val > c.val {
        res = c
        res.choice = 3
    }
    return res
}

// deduce the result and print the specific operations
func printResult(dp [][]Node, s1, s2 string) {
    rows := len(dp)
    cols := len(dp[0])
    i, j := rows - 1, cols - 1
    fmt.Printf("Change s1=%s to s2=%s:\n\n", s1, s2)
    for i != 0 && j != 0 {
        c1 := s1[i-1]
        c2 := s2[j-1]
        choice := dp[i][j].choice
        fmt.Printf("s1[%d]:", i-1)
        switch choice {
        case 0:
            // skip, then both pointers move forward
            fmt.Printf("skip '%c'\n", c1)
            i--
            j--
        case 1:
            // insert s2[j] into s1[i], then the s2 pointer moves forward
            fmt.Printf("insert '%c'\n", c2)
            j--
        case 2:
            // delete s1[i], then the s1 pointer moves forward
            fmt.Printf("delete '%c'\n", c1)
            i--
        case 3:
            // replace s1[i] with s2[j], then both pointers move forward
            fmt.Printf("replace '%c' with '%c'\n", c1, c2)
            i--
            j--
        }
    }
    // if s1 is not finished, the remaining characters need to be deleted
    for i > 0 {
        fmt.Printf("s1[%d]:", i-1)
        fmt.Printf("delete '%c'\n", s1[i-1])
        i--
    }
    // if s2 is not finished, the remaining characters need to be inserted into s1
    for j > 0 {
        fmt.Printf("s1[0]:")
        fmt.Printf("insert '%c'\n", s2[j-1])
        j--
    }
}

function minDistance(s1, s2) {
    var m = s1.length, n = s2.length;
    var dp = Array.from({length: m + 1}, () => Array(n + 1).fill(new Node()));
    // base case
    for (var i = 0; i <= m; i++) {
        // converting s1 to s2 requires only deleting one character
        dp[i][0] = new Node(i, 2);
    }
    for (var j = 1; j <= n; j++) {
        // converting s1 to s2 requires only inserting one character
        dp[0][j] = new Node(j, 1);
    }
    // state transition equation
    for (var i = 1; i <= m; i++) {
        for (var j = 1; j <= n; j++) {
            if (s1.charAt(i-1) == s2.charAt(j-1)) {
                // if two characters are the same, nothing needs to be done
                var node = dp[i - 1][j - 1];
                dp[i][j] = new Node(node.val, 0);
            } else {
                // otherwise, record the operation with the minimum cost
                dp[i][j] = minNode(
                    dp[i - 1][j],
                    dp[i][j - 1],
                    dp[i-1][j-1]
                );
                // and increment the edit distance by one
                dp[i][j].val++;
            }
        }
    }
    // deduce the specific operation process based on the dp table and print it
    printResult(dp, s1, s2);
    return dp[m][n].val;
}

// calculate the operation with the minimum cost among delete, insert, replace
function minNode(a, b, c) {
    var res = a;
    if (res.val > b.val) {
        res = b;
        res.choice = 1;
    }
    if (res.val > c.val) {
        res = c;
        res.choice = 3;
    }
    return res;
}


// deduce the result and print the specific operations
function printResult(dp, s1, s2) {
    var rows = dp.length;
    var cols = dp[0].length;
    var i = rows - 1, j = cols - 1;
    console.log(`Change s1=${s1} to s2=${s2}:\n`);
    while (i != 0 && j != 0) {
        var c1 = s1[i - 1];
        var c2 = s2[j - 1];
        var choice = dp[i][j].choice;
        console.log(`s1[${i - 1}]:`, end='');
        switch (choice) {
            case 0:
                // skip, then both pointers move forward
                console.log(`skip '${c1}'`);
                i--;
                j--;
                break;
            case 1:
                // insert s2[j] into s1[i], then the s2 pointer moves forward
                console.log(`insert '${c2}'`);
                j--;
                break;
            case 2:
                // delete s1[i], then the s1 pointer moves forward
                console.log(`delete '${c1}'`);
                i--;
                break;
            case 3:
                // replace s1[i] with s2[j], then both pointers move forward
                console.log(`replace '${c1}' with '${c2}'`);
                i--;
                j--;
                break;
        }
    }
    // if s1 is not finished, the remaining characters need to be deleted
    while (i > 0) {
        console.log(`s1[${i - 1}]:`, end='');
        console.log(`delete '${s1[i - 1]}'`);
        i--;
    }
    // if s2 is not finished, the remaining characters need to be inserted into s1
    while (j > 0) {
        console.log(`s1[0]:`, end='');
        console.log(`insert '${s2[j - 1]}'`);
        j--;
    }
}