Save Money on Your Trip: Weighted Shortest Path
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 787. Cheapest Flights Within K Stops | 🟠 |
| 787. Cheapest Flights Within K Stops | 🟠 |
Prerequisites
Before reading this article, you need to learn:
Graduation season brings both happiness and a bit of sadness for the past, and maybe some confusion and hope for the future. But all these feelings will fade with time.
At the end of this wonderful time, you should take a spontaneous graduation trip, enjoy yourself, and give your youth a perfect ending.
This article will teach you a dynamic programming algorithm to help you save money on your graduation trip.
Suppose you are about to start from the city where your school is, travel through several cities, and finally arrive at your company for your new job. How should you plan your route to spend the least on flight tickets?
Let’s look at LeetCode problem 787: Cheapest Flights Within K Stops:
787. Cheapest Flights Within K Stops | LeetCode | 🟠
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
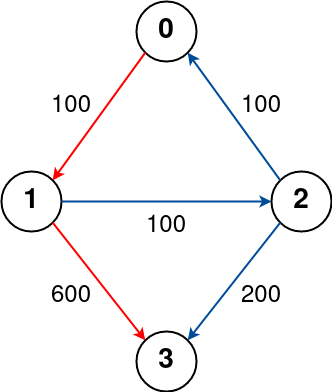
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
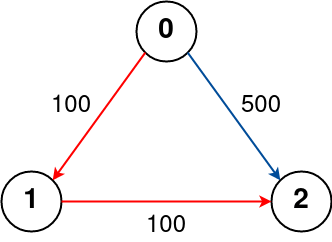
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3:
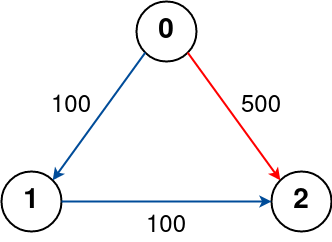
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
The function signature is as follows:
int findCheapestPrice(int n, int[][] flights, int src, int dst, int K);int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K);def findCheapestPrice(n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:func findCheapestPrice(n int, flights [][]int, src int, dst int, K int) int {}var findCheapestPrice = function(n, flights, src, dst, K) {}Clearly, this is a shortest path problem in a weighted directed graph.
In simple terms, you are given a weighted directed graph. You need to find the path from src to dst with the smallest total weight, but the path can have at most K + 1 edges (passing through K nodes means you have K + 1 edges).
Now, let’s analyze the algorithms related to finding the shortest path.