Implement Stack with Queue, Implement Queue with Stack
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 225. Implement Stack using Queues | 🟢 |
| 232. Implement Queue using Stacks | 🟢 |
Prerequisites
Before reading this article, you should first learn:
A queue is a first-in-first-out (FIFO) data structure. A stack is a last-in-first-out (LIFO) data structure. Here is a simple illustration:
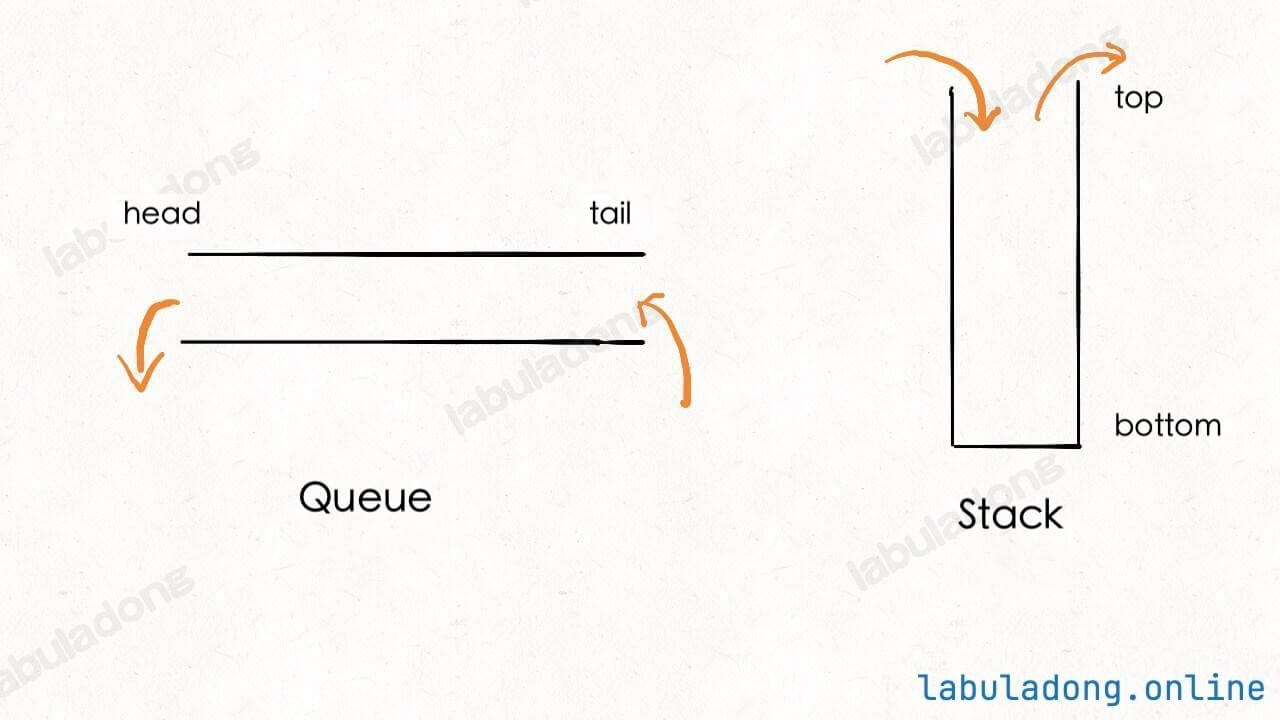
Both of these data structures are usually implemented using arrays or linked lists. Their APIs make them different. For more details, see Principles and Implementation of Queue/Stack.
Today, let's see how to use a stack to build a queue, and how to use a queue to build a stack.
1. Implementing a Queue Using Stacks
LeetCode Problem 232 "Implement Queue using Stacks" asks us to implement the following API:
class MyQueue {
// add element to the end of the queue
public void push(int x);
// remove the element at the front of the queue and return it
public int pop();
// return the front element
public int peek();
// check if the queue is empty
public boolean empty();
}class MyQueue {
public:
// add element to the end of the queue
void push(int x);
// delete the front element of the queue and return it
int pop();
// return the front element
int peek();
// check if the queue is empty
bool empty();
};class MyQueue:
# add element to the back of the queue
def push(self, x: int) -> None:
pass
# remove and return the front element of the queue
def pop(self) -> int:
pass
# return the front element of the queue
def peek(self) -> int:
pass
# check if the queue is empty
def empty(self) -> bool:
passtype MyQueue struct {}
// add element to the end of the queue
func (q *MyQueue) push(x int) {
}
// remove and return the element at the front of the queue
func (q *MyQueue) pop() int {
return 0
}
// return the element at the front of the queue
func (q *MyQueue) peek() int {
}
// check if the queue is empty
func (q *MyQueue) empty() bool {
}var MyQueue = function() {
// add element to the end of the queue
this.push = function(x) {
}
// remove and return the front element of the queue
this.pop = function() {
}
// return the front element of the queue
this.peek = function() {
}
// check if the queue is empty
this.empty = function() {
}
}We can use two stacks, s1 and s2, to build a queue. (The diagram below shows how the stacks are arranged for better understanding.)
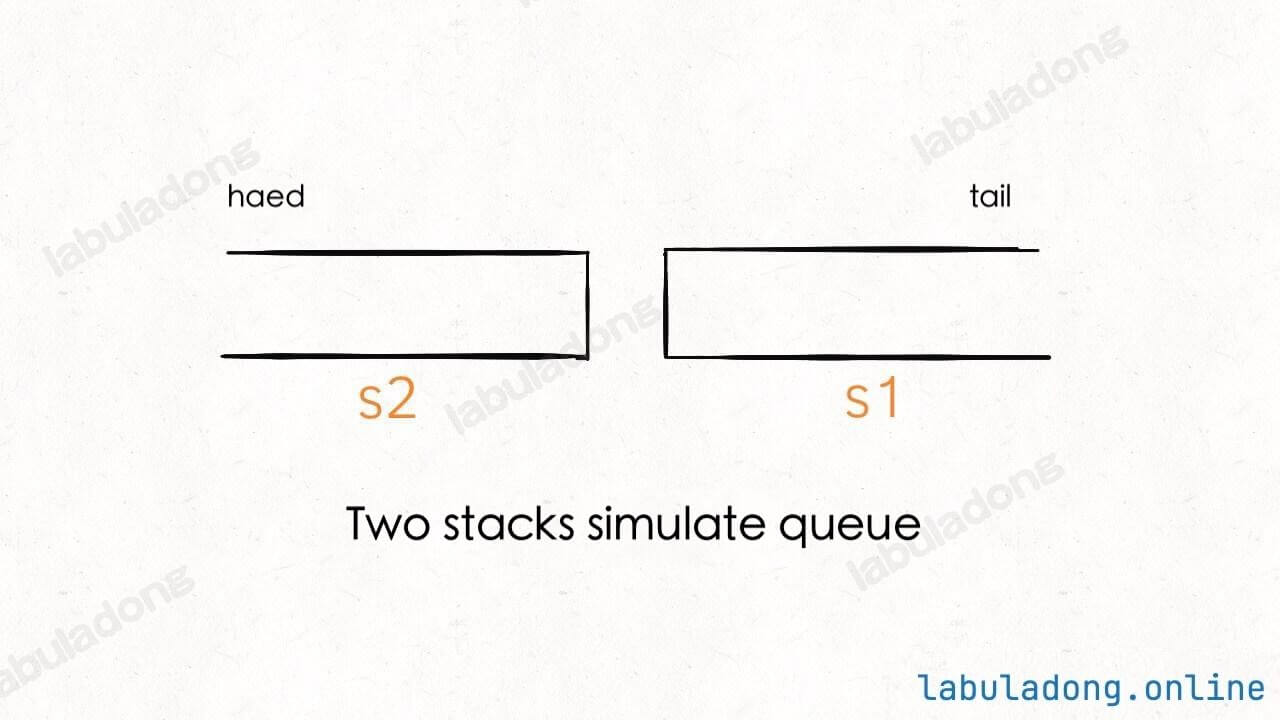
When you call push to add an element to the queue, just push the element onto s1. For example, if you push three elements 1, 2, and 3, the stacks look like this:
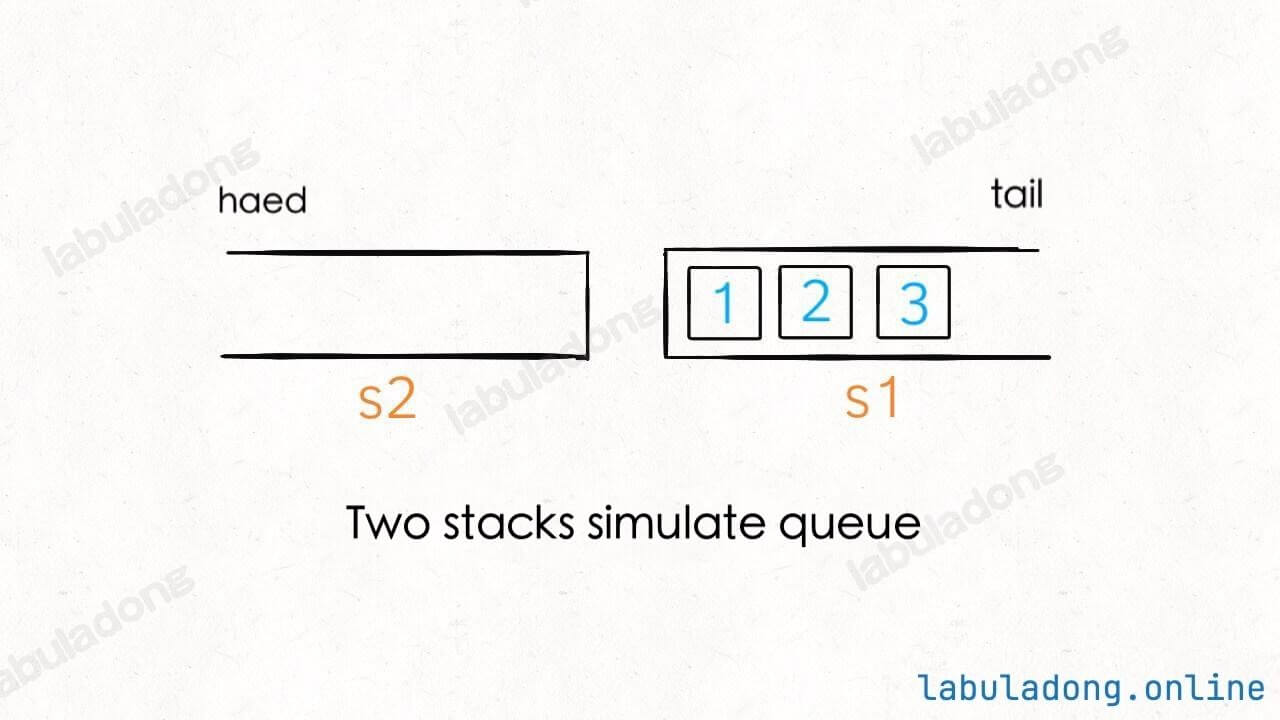
Now, what if you want to use peek to see the front element of the queue? The front of the queue should be 1, but in s1, the number 1 is at the bottom. This is where s2 comes in. When s2 is empty, you can pop all elements from s1 and push them into s2. Now the elements in s2 are in the correct queue order (first in, first out).

When s2 has elements, you can just use pop on s2 to remove the oldest element. This is how you get the pop operation of a queue.
Here is the complete code:
class MyQueue {
private Stack<Integer> s1, s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
// Push element x to the back of the queue.
public void push(int x) {
s1.push(x);
}
// Removes the element from in front of queue and returns that element.
public int pop() {
// call peek first to ensure s2 is not empty
peek();
return s2.pop();
}
// Get the front element.
public int peek() {
if (s2.isEmpty())
// push elements from s1 to s2
while (!s1.isEmpty())
s2.push(s1.pop());
return s2.peek();
}
// Returns whether the queue is empty.
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
}class MyQueue {
private:
stack<int> s1, s2;
public:
MyQueue() {
// Constructor initializes two stacks
}
// Push element x to the back of the queue.
void push(int x) {
s1.push(x);
}
// Removes the element from in front of queue and returns that element.
int pop() {
// call peek first to ensure s2 is not empty
peek();
int topElement = s2.top();
s2.pop();
return topElement;
}
// Get the front element.
int peek() {
if (s2.empty()) {
// push elements from s1 to s2
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
}
return s2.top();
}
// Returns whether the queue is empty.
bool empty() {
return s1.empty() && s2.empty();
}
};class MyQueue:
def __init__(self):
self.s1 = []
self.s2 = []
# Push element x to the back of the queue.
def push(self, x: int) -> None:
self.s1.append(x)
# Removes the element from in front of queue and returns that element.
def pop(self) -> int:
# call peek first to ensure s2 is not empty
self.peek()
return self.s2.pop()
# Get the front element.
def peek(self) -> int:
if not self.s2:
# push elements from s1 to s2
while self.s1:
self.s2.append(self.s1.pop())
return self.s2[-1]
# Returns whether the queue is empty.
def empty(self) -> bool:
return not self.s1 and not self.s2type MyQueue struct {
s1, s2 []int
}
func Constructor() MyQueue {
return MyQueue{
s1: []int{},
s2: []int{},
}
}
// Push element x to the back of the queue.
func (this *MyQueue) Push(x int) {
this.s1 = append(this.s1, x)
}
// Removes the element from in front of queue and returns that element.
func (this *MyQueue) Pop() int {
// call peek first to ensure s2 is not empty
this.Peek()
x := this.s2[len(this.s2)-1]
this.s2 = this.s2[:len(this.s2)-1]
return x
}
// Get the front element.
func (this *MyQueue) Peek() int {
if len(this.s2) == 0 {
// push elements from s1 to s2
for len(this.s1) > 0 {
size := len(this.s1)
this.s2 = append(this.s2, this.s1[size-1])
this.s1 = this.s1[:size-1]
}
}
return this.s2[len(this.s2)-1]
}
// Returns whether the queue is empty.
func (this *MyQueue) Empty() bool {
return len(this.s1) == 0 && len(this.s2) == 0
}var MyQueue = function() {
this.s1 = [];
this.s2 = [];
};
// Push element x to the back of the queue.
MyQueue.prototype.push = function(x) {
this.s1.push(x);
};
// Removes the element from in front of queue and returns that element.
MyQueue.prototype.pop = function() {
// call peek first to ensure s2 is not empty
this.peek();
return this.s2.pop();
};
// Get the front element.
MyQueue.prototype.peek = function() {
if (this.s2.length === 0) {
// push elements from s1 to s2
while (this.s1.length > 0) {
this.s2.push(this.s1.pop());
}
}
return this.s2[this.s2.length - 1];
};
// Returns whether the queue is empty.
MyQueue.prototype.empty = function() {
return this.s1.length === 0 && this.s2.length === 0;
};With this method, we use two stacks to make a queue. The key idea is to let the two stacks work together.
Now, what is the time complexity of these operations?
The peek operation is interesting. When you call peek, it may trigger a while loop, making the time complexity O(N). But in most cases, the while loop is not triggered, so the time complexity is O(1). The pop operation also calls peek, so its time complexity is the same as peek.
In this situation, we can say the worst-case time complexity is O(N), because the while loop might need to move all elements from s1 to s2.
But the amortized time complexity is O(1). Each element will be moved at most once, so on average, every peek operation takes O(1) time per element.
For more on analyzing time complexity, see Practical Analysis of Time and Space Complexity.
2. Implementing a Stack Using a Queue
If using two stacks to make a queue is clever, then using a queue to make a stack is more simple and direct. You only need one queue as the base data structure.
LeetCode Problem 225 “Implement Stack using Queues” asks us to build these APIs:
class MyStack {
// add element to the top of the stack
public void push(int x);
// remove the top element of the stack and return it
public int pop();
// return the top element of the stack
public int top();
// check if the stack is empty
public boolean empty();
}class MyStack {
// add element to the top of the stack
void push(int x);
// remove the top element of the stack and return it
int pop();
// return the top element of the stack
int top();
// check if the stack is empty
bool empty();
};class MyStack:
# push element onto stack
def push(self, x: int) -> None:
pass
# remove the top element and return it
def pop(self) -> int:
pass
# return the top element
def top(self) -> int:
pass
# check if the stack is empty
def empty(self) -> bool:
passtype MyStack struct {
}
// add element to the top of the stack
func (s *MyStack) Push(x int) {
}
// remove the top element of the stack and return it
func (s *MyStack) Pop() int {
}
// return the top element of the stack
func (s *MyStack) Top() int {
}
// check if the stack is empty
func (s *MyStack) Empty() bool {
}var MyStack = function() {
// add element to the top of the stack
this.push = function(x) {
};
// remove the top element of the stack and return it
this.pop = function() {
};
// return the top element of the stack
this.top = function() {
};
// check if the stack is empty
this.empty = function() {
};
};Let's start with the push API. Just add the element to the queue and record the last element of the queue. The last element is like the top of the stack. If you want to use top to see the top element, you can return it directly:
class MyStack {
Queue<Integer> q = new LinkedList<>();
int top_elem = 0;
// add element to the top of the stack
public void push(int x) {
// x is the tail of the queue, which is the top of the stack
q.offer(x);
top_elem = x;
}
// return the top element of the stack
public int top() {
return top_elem;
}
public boolean empty() {
return q.isEmpty();
}
}#include<queue>
using namespace std;
class MyStack {
queue<int> q;
int top_elem = 0;
public:
// add element to the top of the stack
void push(int x) {
// x is the tail of the queue, which is the top of the stack
q.push(x);
top_elem = x;
}
// return the top element of the stack
int top() {
return top_elem;
}
bool empty() {
return q.empty();
}
};class MyStack:
def __init__(self):
# use a queue q to implement a stack
self.q = []
# top element of the stack
self.top_elem = 0
# add an element to the top of the stack
def push(self, x: int) -> None:
# x is the rear of the queue, which is the top of the stack
self.q.append(x)
self.top_elem = x
# return the top element of the stack
def top(self) -> int:
return self.top_elem
# check if the stack is empty
def empty(self) -> bool:
return len(self.q) == 0import "container/list"
type MyStack struct {
q *list.List
top_elem int
}
// MyStack constructor
func Constructor() MyStack {
return MyStack{q: list.New()}
}
// push an element onto the stack
func (this *MyStack) Push(x int) {
// x is the tail of the queue, which is the top of the stack
this.q.PushBack(x)
this.top_elem = x
}
// return the top element of the stack
func (this *MyStack) Top() int {
return this.top_elem
}
// check if the stack is empty
func (this *MyStack) Empty() bool {
return this.q.Len() == 0
}var MyStack = function() {
this.q = [];
this.top_elem = 0;
};
// push element to the top of the stack
MyStack.prototype.push = function(x) {
// x is the tail of the queue, which is the top of the stack
this.q.push(x);
this.top_elem = x;
};
// return the top element of the stack
MyStack.prototype.top = function() {
return this.top_elem;
};
MyStack.prototype.empty = function() {
return this.q.length === 0;
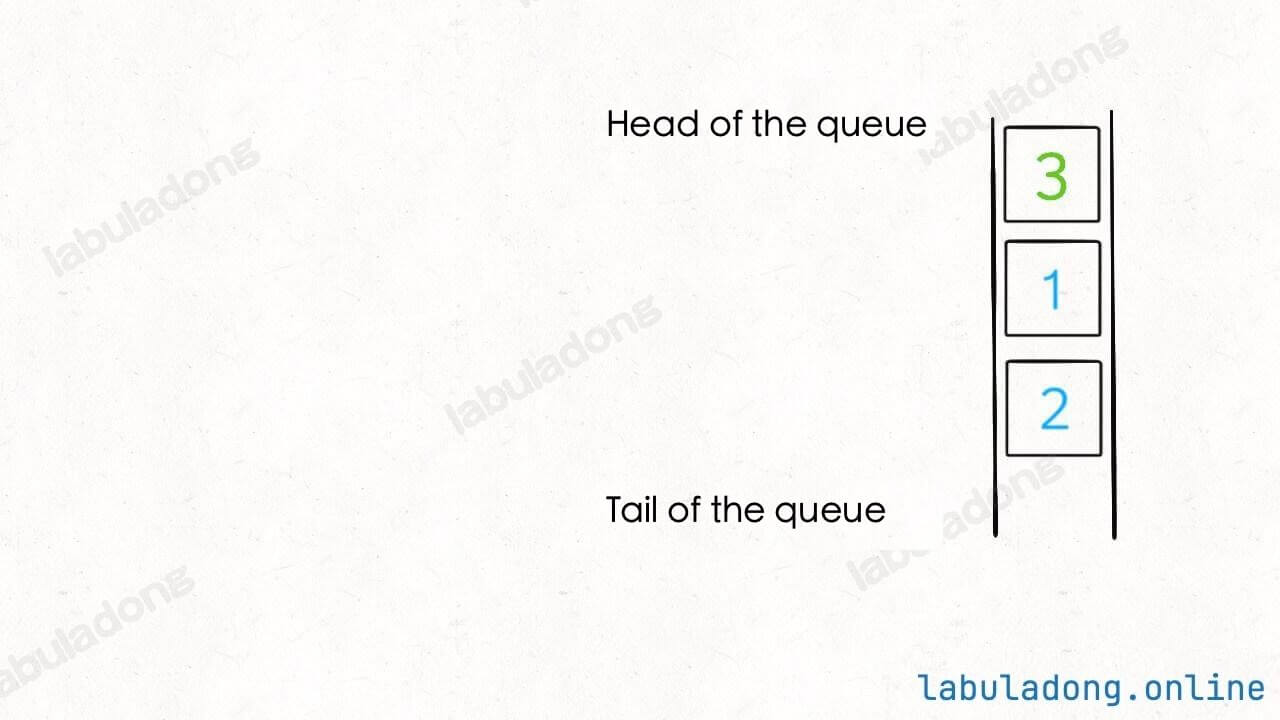
};Our base data structure is a queue, which is first in, first out. Each time you pop, you can only take from the front. But a stack is last in, first out, which means the pop API needs to take from the end:
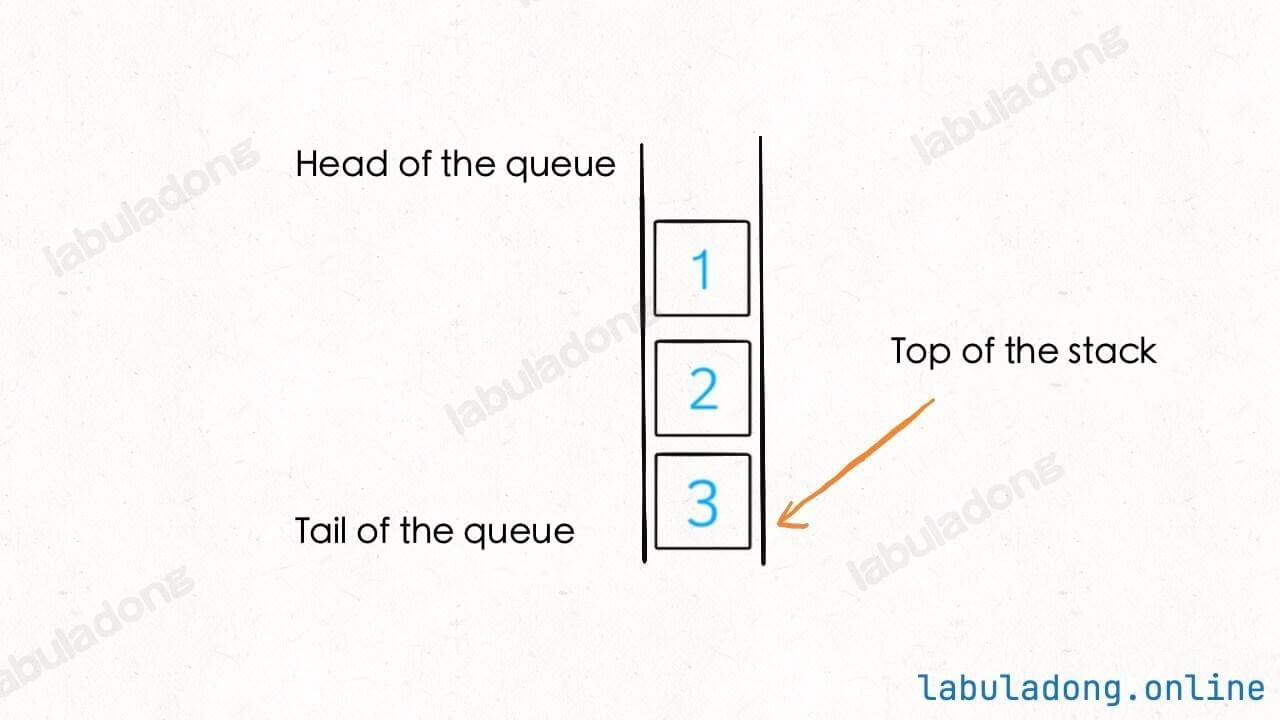
The solution is simple. Take all the elements from the front of the queue and add them to the end, except the last one. This way, the original last element moves to the front, so you can take it out:
class MyStack {
// To save space, the code above is omitted...
// Delete the top element of the stack and return it
public int pop() {
int size = q.size();
while (size > 1) {
q.offer(q.poll());
size--;
}
// The previous last element of the queue is now at the front
return q.poll();
}
}class MyStack {
// To save space, the code above is omitted...
// remove and return the top element of the stack
int pop() {
int size = q.size();
while (size > 1) {
q.push(q.front());
q.pop();
size--;
}
// the previous last element of the queue is now at the front
int res = q.front();
q.pop();
return res;
}
};class MyStack:
# To save space, the code provided above is omitted...
# Remove the top element of the stack and return it
def pop(self):
size = len(self.q)
while size > 1:
self.q.append(self.q.pop(0))
size -= 1
# The previous last element of the queue is now at the front
return self.q.pop(0)// To save space, the code given above is omitted...
func (this *MyStack) Pop() int {
size := len(this.q)
for size > 1 {
this.q = append(this.q, this.q[0])
this.q = this.q[1:]
size--
}
// The previous tail element of the queue has moved to the front
poppedElement := this.q[0]
this.q = this.q[1:]
return poppedElement
}// To save space, the code portion given above is omitted...
MyStack.prototype.pop = function() {
var size = this.q.length;
while (size > 1) {
this.q.push(this.q.shift());
size--;
}
// the previous tail element of the queue is now at the head
return this.q.shift();
};There is one small problem. The last element of the queue is moved to the front and removed, but the top_elem variable is not updated. We need to make a small change:
class MyStack {
// To save space, the code given above is omitted...
// remove the top element and return it
public int pop() {
int size = q.size();
// leave the last 2 elements
while (size > 2) {
q.offer(q.poll());
size--;
}
// record the new last element
top_elem = q.peek();
q.offer(q.poll());
// remove the previous last element
return q.poll();
}
}class MyStack {
// To save space, the code given above is omitted...
// Remove the top element of the stack and return it
public:
int pop() {
int size = q.size();
// Leave the last 2 elements in the queue
while (size > 2) {
q.push(q.front());
q.pop();
size--;
}
// Record the new last element of the queue
top_elem = q.front();
q.push(q.front());
q.pop();
// Remove the previous last element of the queue
int target = q.front();
q.pop();
return target;
}
};class MyStack:
# To save space, the code given above is omitted...
# Remove the top element of the stack and return it
def pop(self):
size = len(self.q)
# Keep the last 2 elements of the queue
while size > 2:
self.q.append(self.q.pop(0))
size -= 1
# Record the new last element of the queue
self.top_elem = self.q[0]
self.q.append(self.q.pop(0))
# Remove the previous last element of the queue
return self.q.pop(0)// To save space, the code given above is omitted...
// Remove the top element of the stack and return it
func (this *MyStack) Pop() int {
size := len(this.q)
// Leave the last 2 elements in the queue
for size > 2 {
this.q = append(this.q, this.q[0])
this.q = this.q[1:]
size--
}
// Record the new last element in the queue
top_elem := this.q[0]
this.q = append(this.q, this.q[0])
this.q = this.q[1:]
// Remove the previous last element in the queue
result := this.q[0]
this.q = this.q[1:]
return result
}// omit the previously given code part...
// remove the top element of the stack and return it
MyStack.prototype.pop = function() {
var size = this.q.length;
// leave the last 2 elements in the queue
while (size > 2) {
this.q.push(this.q.shift());
size--;
}
// record the new last element of the queue
this.top_elem = this.q[0];
this.q.push(this.q.shift());
// remove the previous last element of the queue
return this.q.shift();
}Now it works. Here is the complete code:
class MyStack {
Queue<Integer> q = new LinkedList<>();
int top_elem = 0;
// Push element x onto stack
public void push(int x) {
// x is the tail of the queue, which is the top of the stack
q.offer(x);
top_elem = x;
}
// Removes the element on top of the stack and returns that element
public int top() {
return top_elem;
}
// Removes the element on top of the stack
public int pop() {
int size = q.size();
// leave the last 2 elements in the queue
while (size > 2) {
q.offer(q.poll());
size--;
}
// record the new tail element
top_elem = q.peek();
q.offer(q.poll());
// remove the previous tail element
return q.poll();
}
// Returns whether the stack is empty
public boolean empty() {
return q.isEmpty();
}
}class MyStack {
queue<int> q;
int top_elem = 0;
public:
// Push element x onto stack
void push(int x) {
// x is the tail of the queue, which is the top of the stack
q.push(x);
top_elem = x;
}
// Removes the element on top of the stack and returns that element
int top() {
return top_elem;
}
// Removes the element on top of the stack
int pop() {
int size = q.size();
// leave the last 2 elements in the queue
while (size > 2) {
q.push(q.front());
q.pop();
size--;
}
// record the new tail element
top_elem = q.front();
q.push(q.front());
q.pop();
// remove the previous tail element
int result = q.front();
q.pop();
return result;
}
// Returns whether the stack is empty
bool empty() {
return q.empty();
}
};from collections import deque
class MyStack:
def __init__(self):
self.q = deque()
self.top_elem = 0
# Push element x onto stack
def push(self, x: int) -> None:
# x is the tail of the queue, which is the top of the stack
self.q.append(x)
self.top_elem = x
# Removes the element on top of the stack and returns that element
def top(self) -> int:
return self.top_elem
# Removes the element on top of the stack
def pop(self) -> int:
size = len(self.q)
# leave the last 2 elements in the queue
while size > 2:
self.q.append(self.q.popleft())
size -= 1
# record the new tail element
self.top_elem = self.q[0]
self.q.append(self.q.popleft())
# remove the previous tail element
return self.q.popleft()
# Returns whether the stack is empty
def empty(self) -> bool:
return not self.qtype MyStack struct {
q []int
top_elem int
}
// Constructor initializes the stack
func Constructor() MyStack {
return MyStack{q: []int{}}
}
// Push element x onto stack
func (this *MyStack) Push(x int) {
// x is the tail of the queue, which is the top of the stack
this.q = append(this.q, x)
this.top_elem = x
}
// Returns the element on top of the stack
func (this *MyStack) Top() int {
return this.top_elem
}
// Removes the element on top of the stack
func (this *MyStack) Pop() int {
size := len(this.q)
// leave the last 2 elements in the queue
for size > 2 {
this.q = append(this.q, this.q[0])
this.q = this.q[1:]
size--
}
// record the new tail element
this.top_elem = this.q[0]
this.q = append(this.q, this.q[0])
this.q = this.q[1:]
// remove the previous tail element
res := this.q[0]
this.q = this.q[1:]
return res
}
// Returns whether the stack is empty
func (this *MyStack) Empty() bool {
return len(this.q) == 0
}var MyStack = function() {
this.q = [];
this.top_elem = 0;
};
// Push element x onto stack
MyStack.prototype.push = function(x) {
// x is the tail of the queue, which is the top of the stack
this.q.push(x);
this.top_elem = x;
};
// Removes the element on top of the stack and returns that element
MyStack.prototype.top = function() {
return this.top_elem;
};
// Removes the element on top of the stack
MyStack.prototype.pop = function() {
let size = this.q.length;
// leave the last 2 elements in the queue
while (size > 2) {
this.q.push(this.q.shift());
size--;
}
// record the new tail element
this.top_elem = this.q[0];
this.q.push(this.q.shift());
// remove the previous tail element
return this.q.shift();
};
// Returns whether the stack is empty
MyStack.prototype.empty = function() {
return this.q.length === 0;
};It is clear that when you use a queue to make a stack, the pop operation takes O(N) time, and the other operations are O(1).
In my opinion, using a queue to make a stack is not very interesting, but using two stacks to make a queue is a good thing to learn.

After moving elements from stack s1 to s2, the elements in s2 become first in, first out, just like a queue. This is a bit like “two negatives make a positive” and is not easy to think of at first.