Binary Tree in Action (Serialization)

This is the third article after Binary Tree Key Concepts (Overview). The previous article, Binary Tree Key Concepts (Construction), taught you how to build binary trees. In this article, we will increase the difficulty and learn how to "serialize" and "deserialize" a binary tree.

To explain serialization and deserialization, let's start with the JSON data format.

JSON is used everywhere. For example, we often serialize a struct in code into a JSON string, save it in cache, or send it over the network. The receiver gets the JSON string and deserializes it to get the original data.

This is the purpose of serialization and deserialization: use a certain format to organize data, so the data is independent of any programming language.

Now, imagine you have a binary tree in Java. You want to save it in some way, and then use C++ to read and restore this binary tree. How can you do this? You need to serialize and deserialize the binary tree.

0. Preorder/Inorder/Postorder and Uniqueness of Binary Tree

Before we look at real problems, let’s think: what kind of serialized data can be deserialized to a unique binary tree?

For example, if you are given the preorder traversal of a binary tree, can you restore the original binary tree from it?

The answer is: sometimes you can, sometimes you cannot. It depends on whether the preorder result includes information about null pointers. If you include nulls, you can rebuild the tree uniquely. If not, you cannot.

For example, if your preorder result is [1,2,3,4,5] and does not include nulls, then both trees below have the same preorder result:

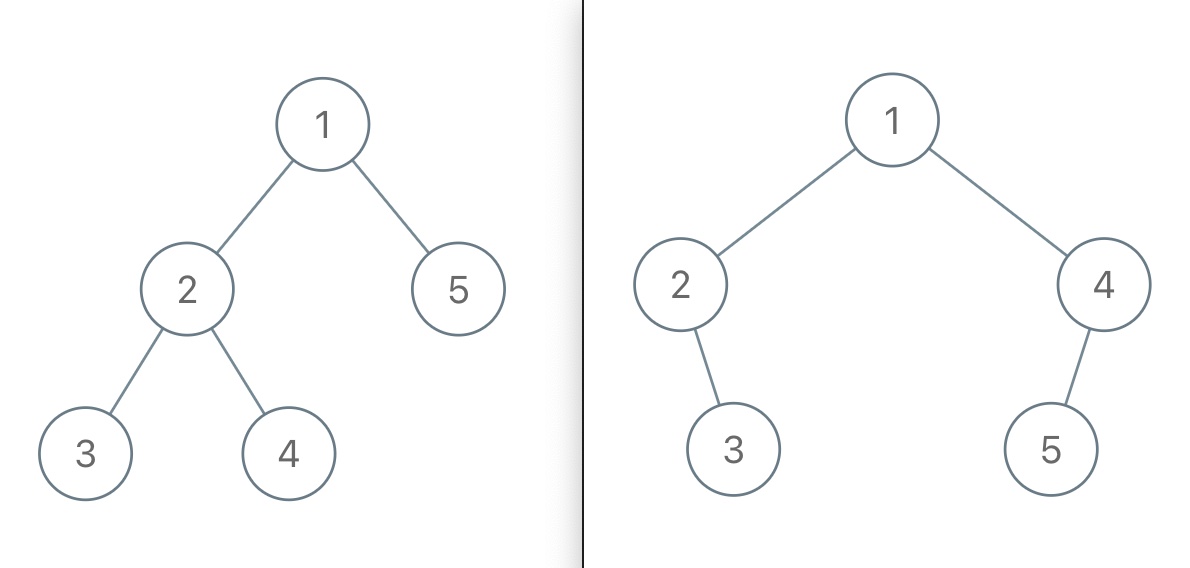
So, if you do not include nulls, you cannot restore a unique binary tree from the preorder traversal.

But if your preorder result includes null pointers (like using # for null), then you can rebuild the unique binary tree. For example, for the left tree above, the preorder result is [1,2,3,#,#,4,#,#,5,#,#]. For the right tree, it is [1,2,#,3,#,#,4,5,#,#,#]. Now they are different.

Maybe you think: "So if I always add nulls, I can always rebuild the tree." Unfortunately, that is not always true. Even if you include nulls, only preorder and postorder traversals can uniquely restore a binary tree. Inorder traversal cannot.

We will talk more about this later. For now, the reason is: preorder and postorder tell you where the root is, but inorder does not.

For example, the two trees below obviously have different structures, but their inorder traversals are both [#,1,#,1,#], so you cannot tell them apart:

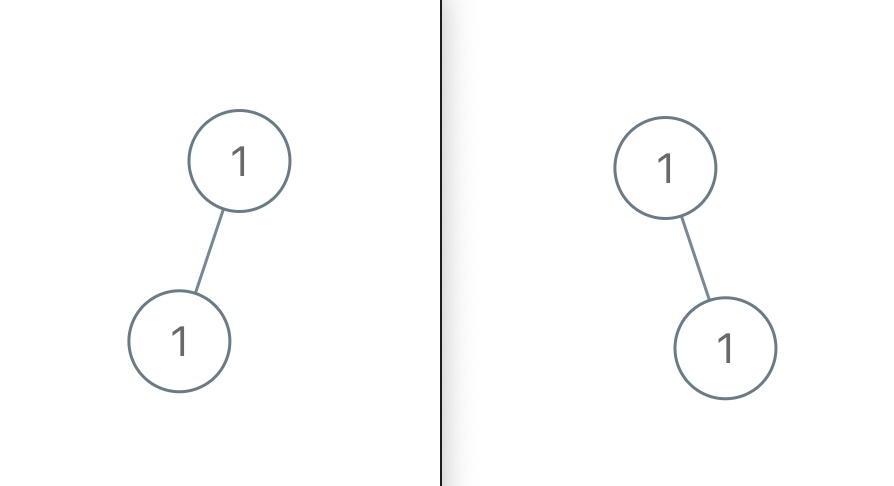
To summarize, if the binary tree nodes have unique values:

1. If your serialized result does not include nulls and only has one kind of traversal, you cannot restore a unique binary tree.

2. If your serialized result does not include nulls and you have two kinds of traversals, there are two cases:

   2.1. If you have preorder and inorder, or postorder and inorder, then you can restore a unique binary tree.

   2.2. If you have preorder and postorder, you cannot restore a unique binary tree.

3. If your serialized result includes nulls and only has one kind of traversal, there are two cases:

   3.1. If you have preorder or postorder, you can restore a unique binary tree.

   3.2. If you have inorder, you cannot restore a unique binary tree.

I mention these conclusions so you can remember them. Later, you will meet related problems, and you can come back to these notes for a deeper understanding. Now let’s look at the specific problems.

1. Problem Description

LeetCode problem 297, "Serialize and Deserialize Binary Tree", gives you the root node root of a binary tree. You need to implement a class like this:

public class Codec {

    // serialize a binary tree into a string
    public String serialize(TreeNode root) {}

    // deserialize a string into a binary tree
    public TreeNode deserialize(String data) {}
}

class Codec {
public:
    // serialize a binary tree into a string
    string serialize(TreeNode* root);

    // deserialize a string into a binary tree
    TreeNode* deserialize(string data);
};

class Codec:
    
    # serialize a binary tree into a string
    def serialize(self, root: TreeNode) -> str:
        pass

    # deserialize a string into a binary tree
    def deserialize(self, data: str) -> TreeNode:
        pass

type Codec struct{}

// serialize a binary tree into a string
func (codec *Codec) serialize(root *TreeNode) string {}

// deserialize a string into a binary tree
func (codec *Codec) deserialize(data string) *TreeNode {}

var Codec = function () {
    
    // serialize a binary tree into a string
    this.serialize = function (root) {}
    
    // deserialize a string into a binary tree
    this.deserialize = function (data) {}
};

You can use the serialize method to turn the binary tree into a string, and use the deserialize method to turn the string back into a binary tree. You can choose any format you want for serialization and deserialization.

For example, given this binary tree:

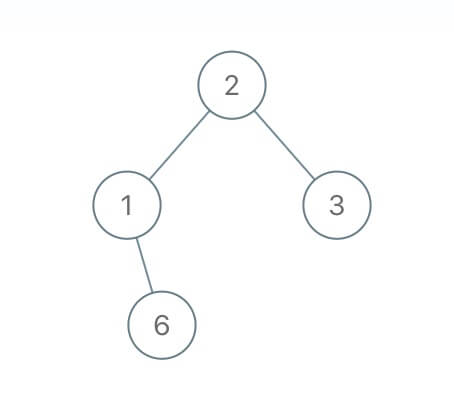
The serialize method might turn it into the string 2,1,#,6,#,#,3,#,#, where # means a null pointer. If you give this string to the deserialize method, it can restore the same binary tree.

In other words, these two methods are used together. You just need to make sure they work with each other.

Think about it: a binary tree is a two-dimensional structure, but the serialized string is a one-dimensional list. Serialization is just "flattening" the tree. It mainly tests your understanding of binary tree traversal.

What are the ways to traverse a binary tree? There are recursive ways like preorder, inorder, and postorder traversal. There is also iterative level-order traversal. In this article, we will try all these ways to implement the serialize and deserialize methods.

2. Preorder Traversal Solution

In the previous article Binary Tree Traversal Basics, we talked about several ways to traverse a binary tree. If we collect nodes in preorder, we get the preorder traversal result:

LinkedList<Integer> res;

void traverse(TreeNode root) {
    if (root == null) {
        // temporarily use the number -1 to represent the null pointer
        res.addLast(-1);
        return;
    }

    // ****** pre-order position ********
    res.addLast(root.val);
    // ***********************

    traverse(root.left);
    traverse(root.right);
}

list<int> res;
void traverse(TreeNode* root) {
    if (root == nullptr) {
        // temporarily use the number -1 to represent the null pointer
        res.push_back(-1);
        return;
    }

    // ****** pre-order position ********
    res.push_back(root->val);
    // ***********************

    traverse(root->left);
    traverse(root->right);
}

res = []

def traverse(root):
    if root is None:
        # temporarily use the number -1 to represent the null pointer
        res.append(-1)
        return

    # ****** pre-order position ******
    res.append(root.val)
    # **********************

    traverse(root.left)
    traverse(root.right)

var res *list.List

func traverse(root *TreeNode) {
	if root == nil {
		// temporarily use the number -1 to represent a null pointer
		res.PushBack(-1)
		return
	}

	// ****** pre-order position ********
	res.PushBack(root.Val)
	// ***********************

	traverse(root.Left)
	traverse(root.Right)
}

var res;
var traverse = function(root) {
    if (root === null) {
        // temporarily use the number -1 to represent the null pointer
        res.push(-1);
        return;
    }

    // ****** pre-order position ********
    res.push(root.val);
    // ***********************

    traverse(root.left);
    traverse(root.right);
}

After calling the traverse function, can you guess the order of elements in the res list? For the tree below (where # means null), we can see what preorder traversal does:

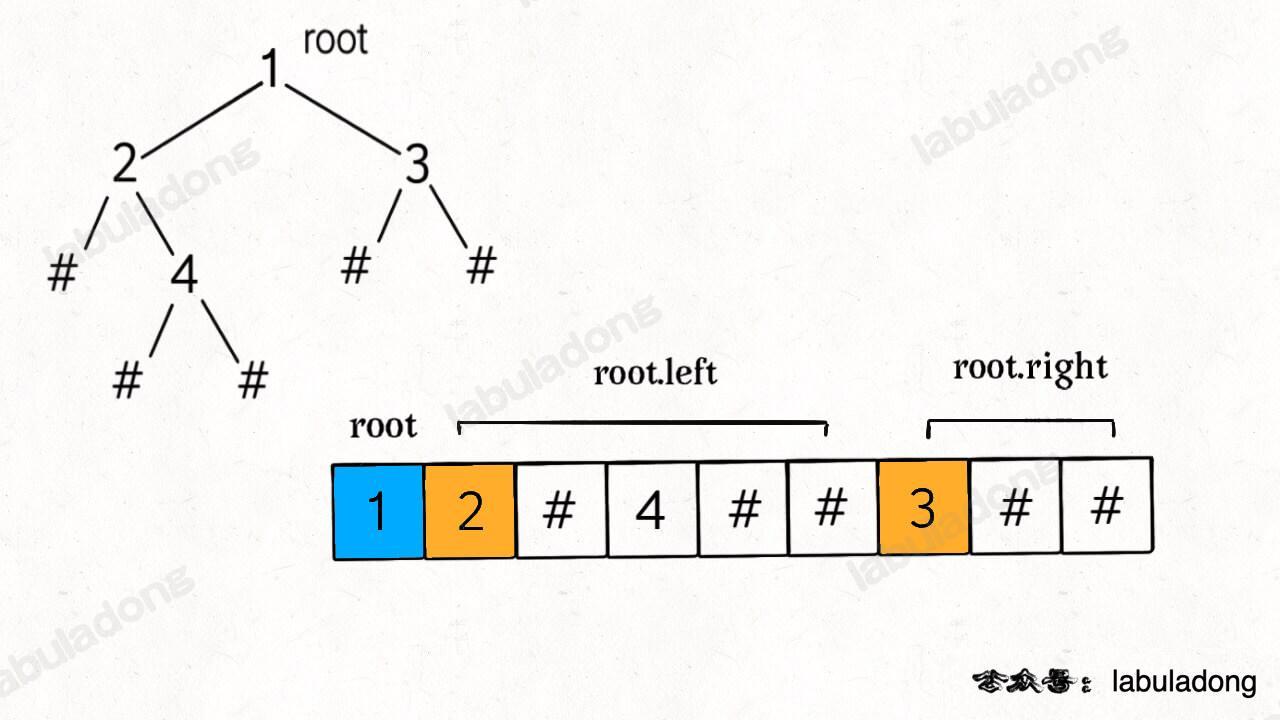
So, res = [1,2,-1,4,-1,-1,3,-1,-1]. This is the "flattened" binary tree as a list, where -1 means null.

Flattening the binary tree into a string is the same idea:

// character representing separator
String SEP = ",";

// character representing null pointer
String NULL = "#";

// for concatenating strings
StringBuilder sb = new StringBuilder();

// flatten the binary tree to a string
void traverse(TreeNode root, StringBuilder sb) {
    if (root == null) {
        sb.append(NULL).append(SEP);
        return;
    }

    // ***** pre-order position *****
    sb.append(root.val).append(SEP);
    // *********************

    traverse(root.left, sb);
    traverse(root.right, sb);
}

// represents the separator character
string SEP = ",";

// represents the null pointer character
string NULL_CHAR = "#";

// used for concatenating strings
std::ostringstream os;

// flatten the binary tree into a string
void traverse(TreeNode* root, std::ostringstream& os) {
    if (root == nullptr) {
        os << NULL_CHAR << SEP;
        return;
    }

    // ***** pre-order position *****
    os << root->val << SEP;
    // *******************

    traverse(root->left, os);
    traverse(root->right, os);
}

# represents the separator character
SEP = ","
# represents the null pointer character
NULL = "#"

# used for concatenating strings
sb = []

# flatten the binary tree into a string
def traverse(root, sb):
    if root == None:
        sb.append(NULL).append(SEP)
        return

    # ***** pre-order position *****
    sb.append(str(root.val)).append(SEP)
    # *******************

    traverse(root.left, sb)
    traverse(root.right, sb)

const (
    // character representing the separator
	SEP = ","
    // character representing null pointer
	NULL = "#"
)

func traverse(root *TreeNode, sb *strings.Builder) {
	if root == nil {
		sb.WriteString(NULL + SEP)
		return
	}

    // ***** pre-order position *****
	sb.WriteString(strconv.Itoa(root.Val) + SEP)
	// *******************

	traverse(root.Left, sb)
	traverse(root.Right, sb)
}

// character representing the delimiter
var SEP = ",";

// character representing null pointer
var NULL = "#";

// used for concatenating strings
var sb = "";

// flatten the binary tree into a string
var traverse = function(root) {
    if (root == null) {
        sb += NULL + SEP;
        return;
    }

    // ***** pre-order position *****
    sb += root.val + SEP;
    // *******************

    traverse(root.left);
    traverse(root.right);
}

This code also collects the preorder result. It uses , as a separator and # for null pointers. After calling the traverse function, the string in sb should be 1,2,#,4,#,#,3,#,#,.

Now, we can write the code for the serialize function:

class Codec {
    String SEP = ",";
    String NULL = "#";

    // main function, serialize the binary tree to a string
    public String serialize(TreeNode root) {
        StringBuilder sb = new StringBuilder();
        _serialize(root, sb);
        return sb.toString();
    }

    // helper function, store the binary tree into StringBuilder
    void _serialize(TreeNode root, StringBuilder sb) {
        if (root == null) {
            sb.append(NULL).append(SEP);
            return;
        }

        // ****** pre-order position ********
        sb.append(root.val).append(SEP);

        // ***********************

        _serialize(root.left, sb);
        _serialize(root.right, sb);
    }
}

class Codec {
public:
    string SEP = ",";
    string NULLSYM = "#";

    
    string serialize(TreeNode* root) {
        string sb;
        _serialize(root, sb);
        return sb;
    }

    // Helper function to serialize the binary tree into the StringBuilder
    void _serialize(TreeNode* root, string& sb) {
        if (root == NULL) {
            sb.append(NULLSYM).append(SEP);
            return;
        }

        // ****** Pre-order position ********
        sb.append(to_string(root->val)).append(SEP);

        // ************************

        _serialize(root->left, sb);
        _serialize(root->right, sb);
    }
};

class Codec:
    SEP = ","
    NULL = "#"

    # Main function, serialize the binary tree into a string
    def serialize(self, root):
        sb = []
        self._serialize(root, sb)
        return "".join(sb)

    # Helper function, store the binary tree into StringBuilder
    def _serialize(self, root, sb):
        if root is None:
            sb.append(self.NULL)
            sb.append(self.SEP)
            return

        # ****** Preorder position ********
        sb.append(str(root.val))
        sb.append(self.SEP)
        # ***********************

        self._serialize(root.left, sb)
        self._serialize(root.right, sb)

type Codec struct {
	SEP   string
	NULL  string
}

func Constructor() Codec {
	return Codec{
		SEP:  ",",
		NULL: "#",
	}
}

// Main function, serialize the binary tree to a string
func (this Codec) serialize(root *TreeNode) string {
	var sb strings.Builder
	this._serialize(root, &sb)
	return sb.String()
}

// Helper function, store the binary tree into StringBuilder
func (this Codec) _serialize(root *TreeNode, sb *strings.Builder) {
	if root == nil {
		sb.WriteString(this.NULL)
		sb.WriteString(this.SEP)
		return
	}

	// ****** Preorder position ********
	sb.WriteString(strconv.Itoa(root.Val))
	sb.WriteString(this.SEP)
	// ***********************

	this._serialize(root.Left, sb)
	this._serialize(root.Right, sb)
}

const SEP = ",";
const NULL = "#";

var serialize = function(root) {
    var sb = [];
    _serialize(root, sb);
    return sb.join('');
};

var _serialize = function(root, sb){
    if(root === null) {
        sb.push(NULL);
        sb.push(SEP);
        return;
    }

    // ****** Preorder position ********
    sb.push(root.val);
    sb.push(SEP);

    // ***********************

    _serialize(root.left, sb);
    _serialize(root.right, sb);
};

Next, let's think about how to write the deserialize function to turn the string back into a binary tree.

First, we can change the string into a list:

String data = "1,2,#,4,#,#,3,#,#,";
String[] nodes = data.split(",");

string data = "1,2,#,4,#,#,3,#,#,";
vector<string> nodes;
stringstream ss(data);
string item;
while(getline(ss, item, ',')) {
    nodes.push_back(item);
}

data = "1,2,#,4,#,#,3,#,#,"
nodes = data.split(",")

data := "1,2,#,4,#,#,3,#,#,"
nodes := strings.Split(data, ",")

var data = "1,2,#,4,#,#,3,#,#,";
var nodes = data.split(",");

Now, the nodes list is the preorder result of the binary tree. The problem becomes: how can we rebuild the binary tree from its preorder result?

From our analysis, the nodes list is a flattened binary tree:

So, for deserialization, we first find the root node, then follow the preorder rules to recursively build the left and right subtrees:

3. Postorder Traversal Solution

4. Inorder Traversal Solution

5. Level Order Traversal Solution