Tricks to Reverse a Linked List Recursively
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 206. Reverse Linked List | 🟢 |
| 25. Reverse Nodes in k-Group | 🔴 |
| 92. Reverse Linked List II | 🟠 |
Reversing a singly linked list with iteration is not hard. But using recursion to do it is a bit tricky. If you add more difficulty, like only reversing a part of the list, can you also use both iteration and recursion? And what if you need to reverse every k nodes in the list? How would you solve it?
This article will solve these linked list problems step by step, from easy to hard. I will use both recursive and iterative methods, and also provide visual panels to help you understand. This will strengthen your thinking about recursion and your ability to work with linked list pointers.
Reverse the Entire Singly Linked List
In LeetCode, the typical structure for a singly linked list is like this:
class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}class ListNode {
public:
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};class ListNode:
def __init__(self, x):
self.val = x
self.next = Nonetype ListNode struct {
Val int
Next *ListNode
}class ListNode {
constructor(val) {
this.val = val;
this.next = null;
}
}Reversing a singly linked list is a basic algorithm problem. LeetCode problem 206, "Reverse Linked List", is about this:
Let's try to solve this problem with different methods.
Iterative Solution
The usual way to solve this problem is with iteration. You use a few pointers to reverse the direction of every node in the linked list. There are no hard parts, just details in pointer operations.
Here is the code with comments. Combined with the visual panel, it should be easy to understand:
class Solution {
// Reverse the linked list starting from head
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
// Due to the structure of a singly linked list, at least three
// pointers are needed to complete the iterative reversal
// cur is the current node being traversed, pre is the
// predecessor node of cur, nxt is the successor node of cur
ListNode pre, cur, nxt;
pre = null; cur = head; nxt = head.next;
while (cur != null) {
// Reverse each node
cur.next = pre;
// Update pointer positions
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
}
// Return the head node after reversal
return pre;
}
}class Solution {
public:
// Reverse the singly linked list starting from head
ListNode* reverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
// Due to the structure of a singly linked list, at least three
// pointers are needed to complete the iterative reversal
// cur is the current node being traversed, pre is the
// predecessor node of cur, nxt is the successor node of cur
ListNode *pre, *cur, *nxt;
pre = nullptr; cur = head; nxt = head->next;
while (cur != nullptr) {
// Reverse each node
cur->next = pre;
// Update pointer positions
pre = cur;
cur = nxt;
if (nxt != nullptr) {
nxt = nxt->next;
}
}
// Return the head node after reversal
return pre;
}
};class Solution:
# Reverse the linked list starting from head
def reverseList(self, head: ListNode) -> ListNode:
if head is None or head.next is None:
return head
# Due to the structure of a singly linked list, at least three
# pointers are needed to complete the iterative reversal
# cur is the current node being traversed, pre is the
# predecessor node of cur, nxt is the successor node of cur
pre, cur, nxt = None, head, head.next
while cur is not None:
# Reverse each node
cur.next = pre
# Update pointer positions
pre = cur
cur = nxt
if nxt is not None:
nxt = nxt.next
# Return the head node after reversal
return pre// Reverse a singly linked list starting from head
func reverseList(head *ListNode) *ListNode {
if head == nil || head.Next == nil {
return head
}
// Due to the structure of a singly linked list, at least three
// pointers are needed to complete the iterative reversal
// cur is the current node being traversed, pre is the
// predecessor node of cur, and nxt is the successor node of cur
var pre, cur, nxt *ListNode
pre, cur, nxt = nil, head, head.Next
for cur != nil {
// Reverse each node
cur.Next = pre
// Update pointer positions
pre = cur
cur = nxt
if nxt != nil {
nxt = nxt.Next
}
}
// Return the head node of the reversed list
return pre
}var reverseList = function(head) {
if (head == null || head.next == null) {
return head;
}
// Due to the structure of a singly linked list, at least three
// pointers are needed to complete the iterative reversal
// cur is the current node being traversed, pre is the
// predecessor node of cur, and nxt is the successor node of cur
var pre, cur, nxt;
pre = null; cur = head; nxt = head.next;
while (cur != null) {
// Reverse each node
cur.next = pre;
// Update pointer positions
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
}
// Return the head node after reversal
return pre;
}You can open the visual panel below and click the line cur.next = pre many times. You will see how the singly linked list is reversed step by step:
Algorithm Visualization
Small Tips for Pointer Operations
The code above is not complex, and there is more than one correct way to write it. But when you work with pointers, there are some simple tips that make your thinking clearer:
When you see code like
nxt.next, you should quickly check ifnxtis null first. Otherwise, you might get a null pointer error.Pay attention to the loop's ending condition. You need to know where each pointer is when the loop ends, so you can return the right answer. If you find it hard to figure out, draw a simple example, like a list with just two nodes,
1->2, and see what happens to the pointers when the loop finishes.
Recursive Solution
The iterative solution above is a bit tedious because of pointer operations, but the idea is still clear. Now, what if you are asked to reverse a singly linked list using recursion? Do you have any ideas?
For beginners, it might be hard to think of a recursive way. That is normal. If you learn the way of thinking in binary tree algorithms later, you may be able to come up with this algorithm yourself.
A binary tree is actually an extension of a singly linked list—it's like a "binary linked list". So the recursive thinking for binary trees also works for linked lists.
The key to reversing a linked list recursively is that this problem has a subproblem structure.
For example, suppose you have a singly linked list 1->2->3->4 with 1 as the head. If you ignore the head node 1 and just look at the sublist 2->3->4, it is still a singly linked list, right?
So, your reverseList function should be able to reverse any linked list given as input. Can you use this function to reverse the sublist 2->3->4 first, and then think about how to attach 1 to the end of the reversed list 4->3->2? This way, you will finish reversing the whole list.
reverseList(1->2->3->4) = reverseList(2->3->4) -> 1This is the idea of "breaking down the problem". Using the definition of the recursive function, we break the original problem into smaller, similar subproblems, and then combine their results to solve the original problem.
There will be special chapters and exercises about this idea later, so we won’t go into more detail here.
Let's look at the code for recursively reversing a singly linked list:
class Solution {
// Definition: Input the head node of a singly linked
// list, reverse the list, and return the new head node
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode last = reverseList(head.next);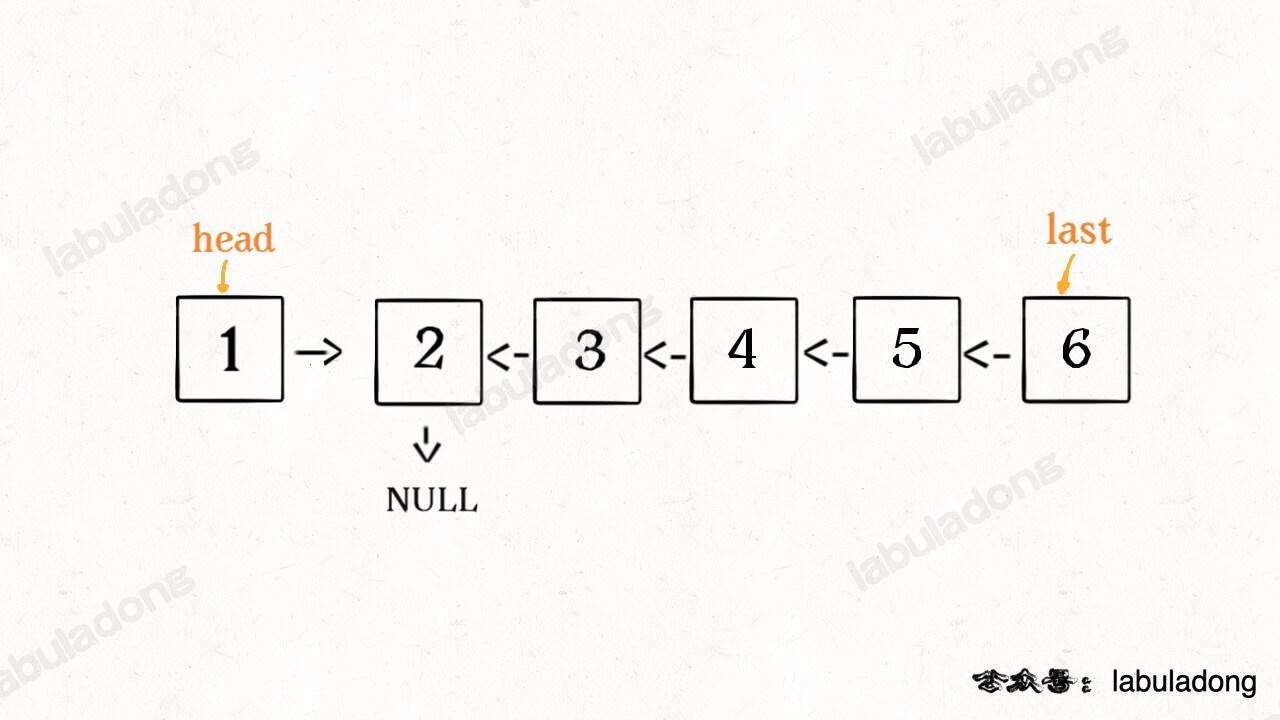 head.next.next = head;
head.next.next = head;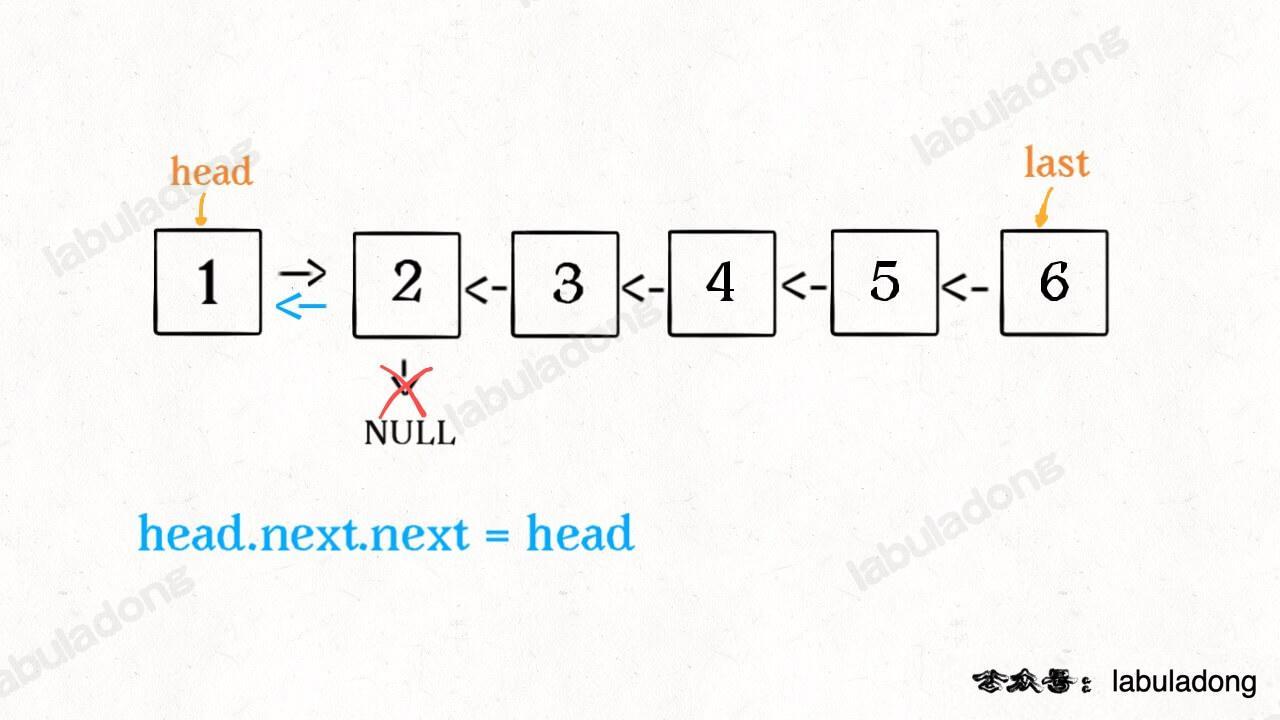 head.next = null;
head.next = null;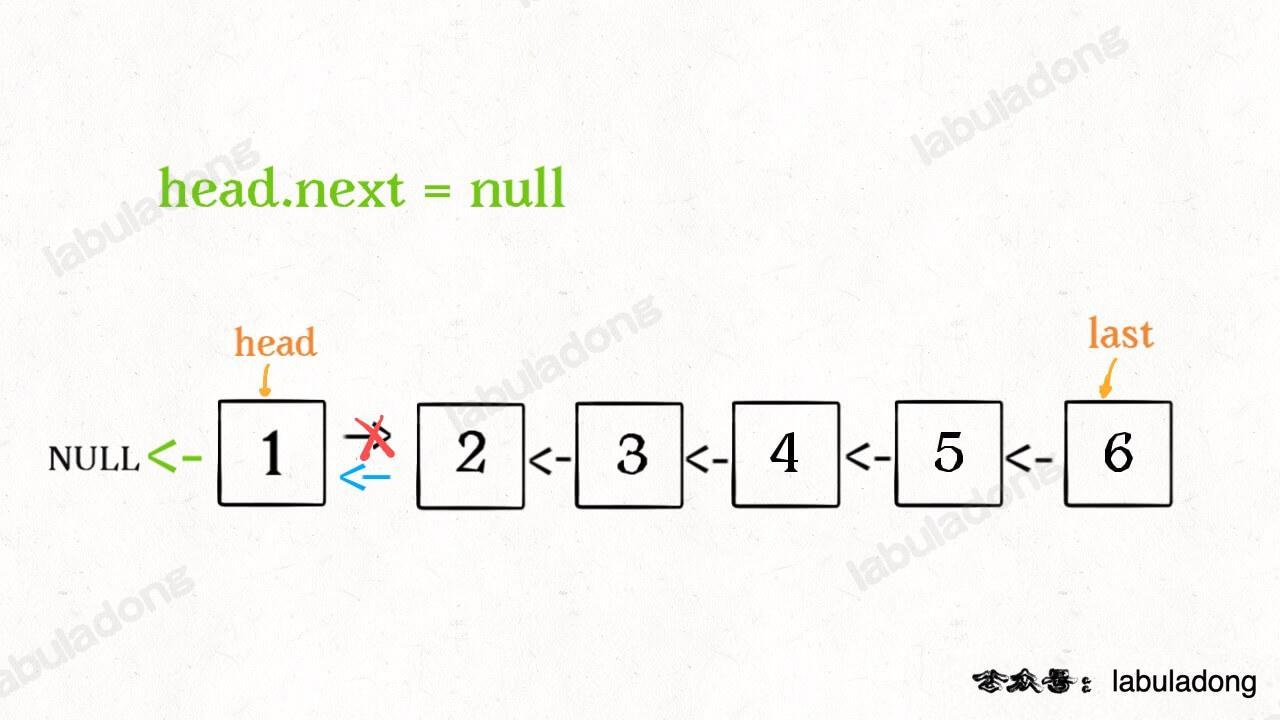 return last;
}
}
return last;
}
}class Solution {
public:
// Definition: Input a head node of a singly linked
// list, reverse the list, and return the new head node
ListNode* reverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* last = reverseList(head->next); head->next->next = head;
head->next->next = head; head->next = nullptr;
head->next = nullptr;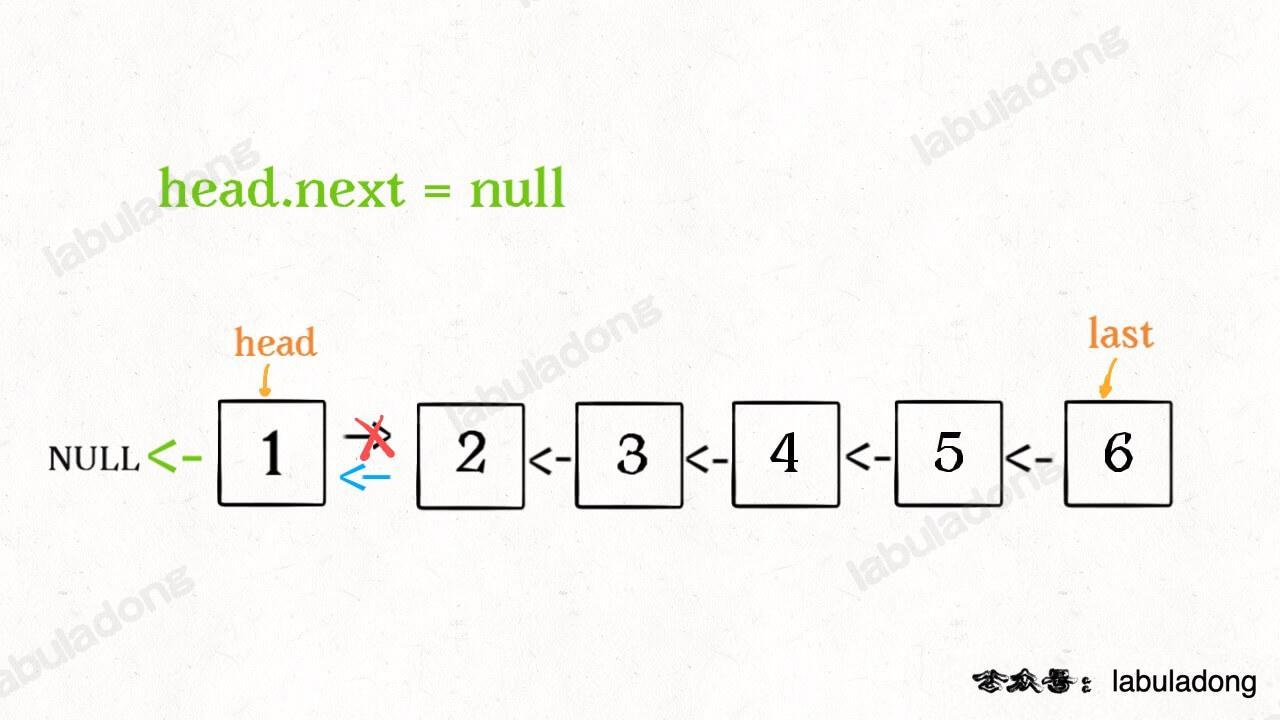 return last;
}
};
return last;
}
};class Solution:
# Definition: Input a head node of a singly linked
# list, reverse the list, and return the new head node
def reverseList(self, head):
if head is None or head.next is None:
return head
last = self.reverseList(head.next)  head.next.next = head
head.next.next = head  head.next = None
head.next = None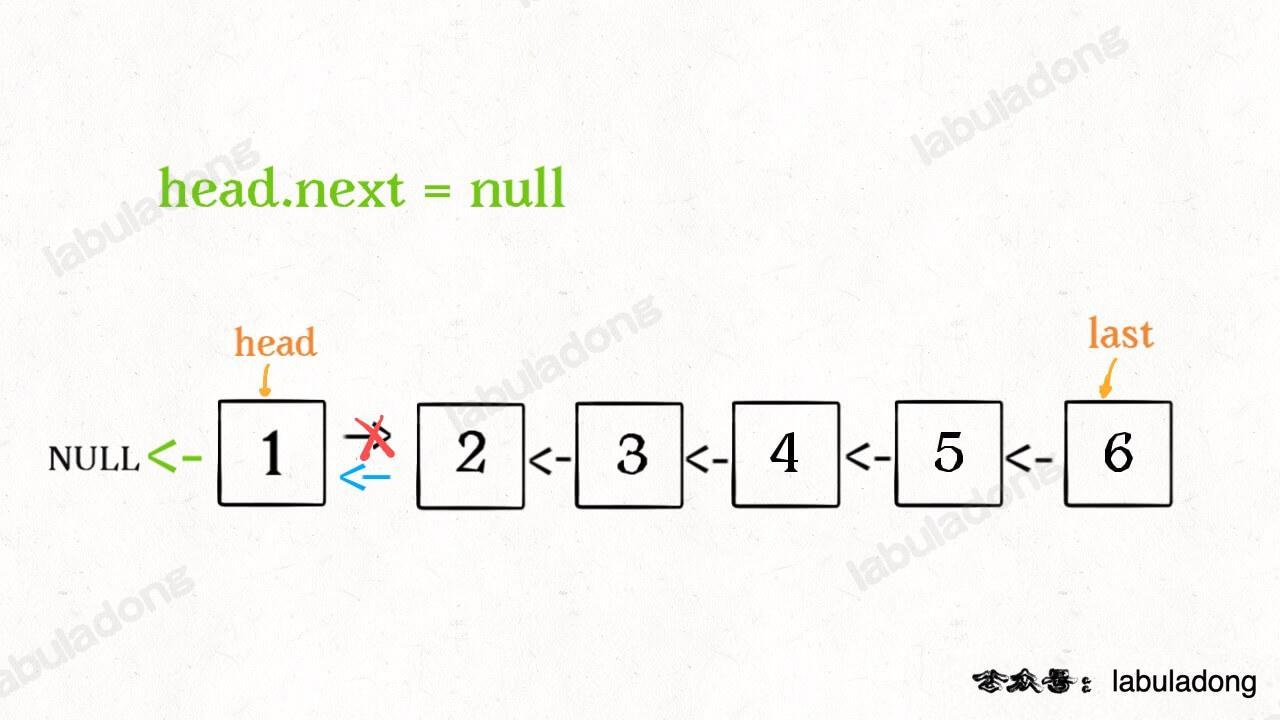 return last
return last// Definition: Input the head node of a singly linked
// list, reverse the list, and return the new head node
func reverseList(head *ListNode) *ListNode {
if head == nil || head.Next == nil {
return head
}
last := reverseList(head.Next) head.Next.Next = head
head.Next.Next = head head.Next = nil
head.Next = nil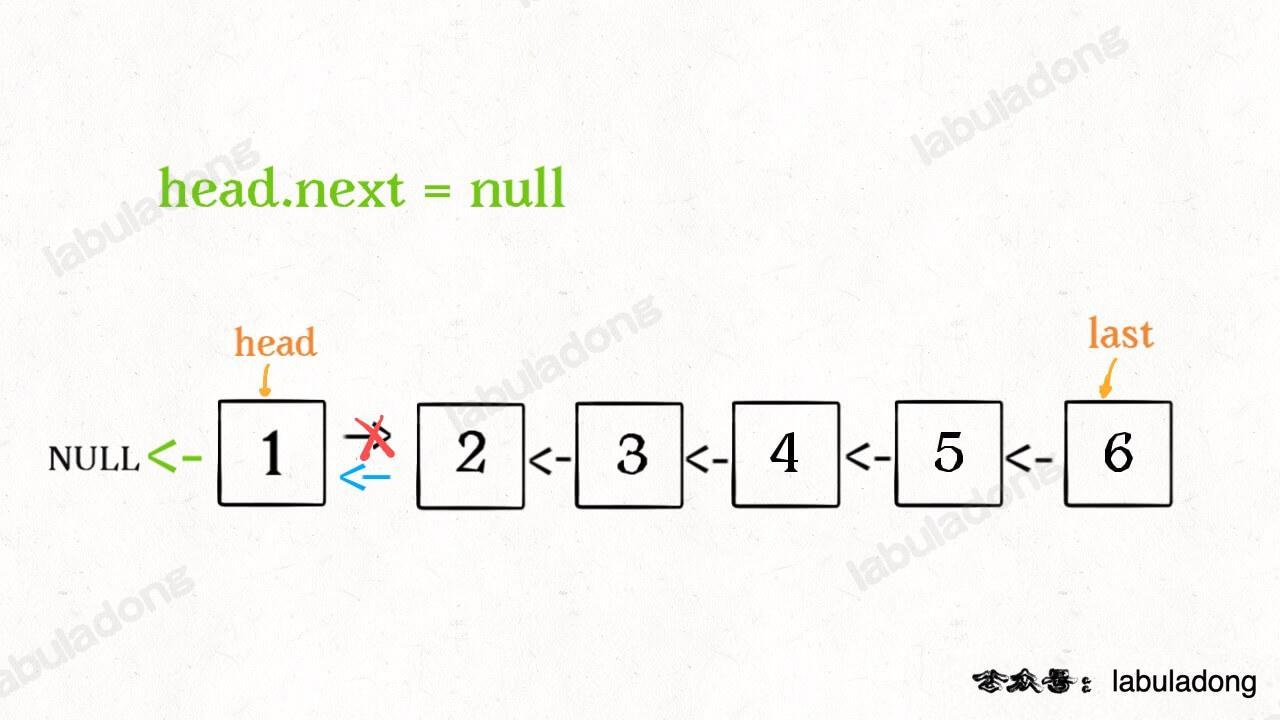 return last
}
return last
}var reverseList = function(head) {
// Definition: Input a head node of a singly linked
// list, reverse the list, and return the new head node
if (head == null || head.next == null) {
return head;
}
var last = reverseList(head.next); head.next.next = head;
head.next.next = head; head.next = null;
head.next = null;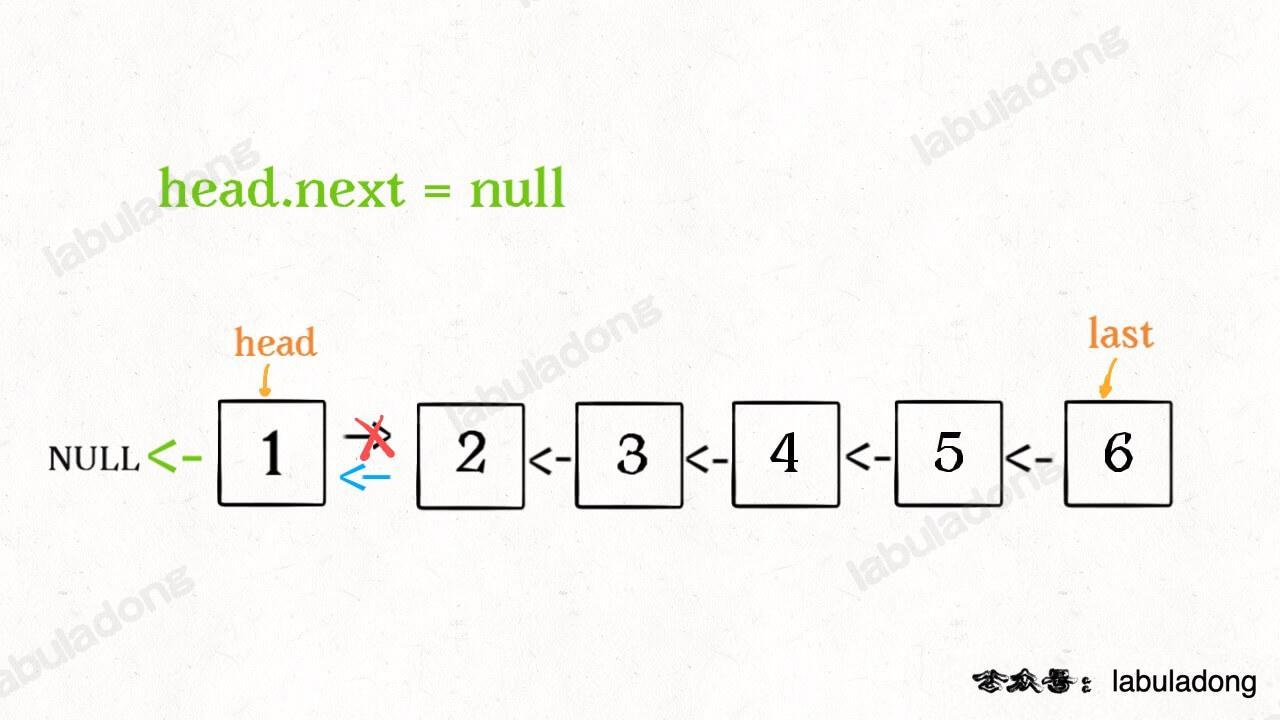 return last;
}
return last;
}This algorithm often shows the beauty and cleverness of recursion. Next, let's explain this code in detail. We will also provide a visual panel so you can explore the recursion yourself.
For recursive algorithms that "break down the problem", the most important thing is to be clear about the definition of the recursive function. Specifically, our reverseList function is defined as:
Given a node head, reverse the list starting from head and return the new head of the reversed list.
Once you understand the function definition, let's look at the problem. For example, we want to reverse this list:
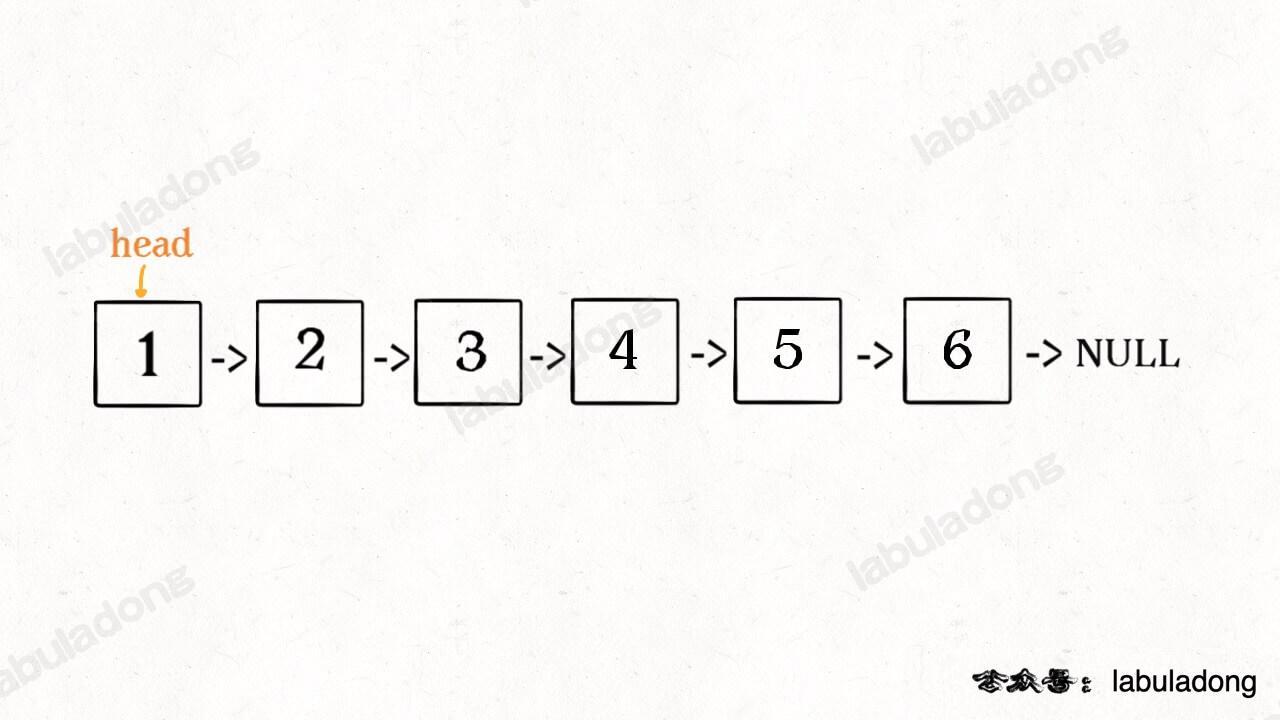
When you call reverseList(head), recursion happens here:
ListNode last = reverseList(head.next);Don’t get lost in recursion (your brain can only hold so many stacks!). Instead, use the function definition to understand what this code does:
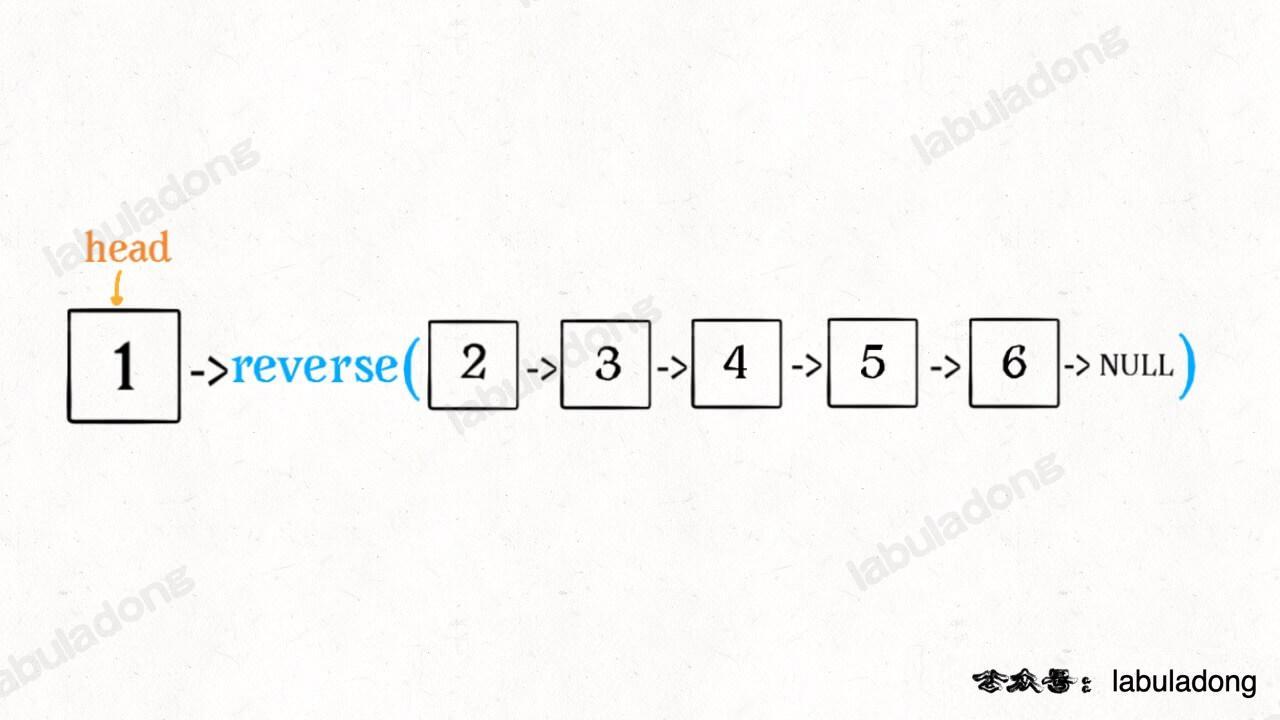
After reverseList(head.next) finishes, the whole list becomes:

And according to the function definition, the reverseList function returns the new head of the reversed list, which we store in the variable last.
Now, look at the next line:
head.next.next = head;
Next:
head.next = null;
return last;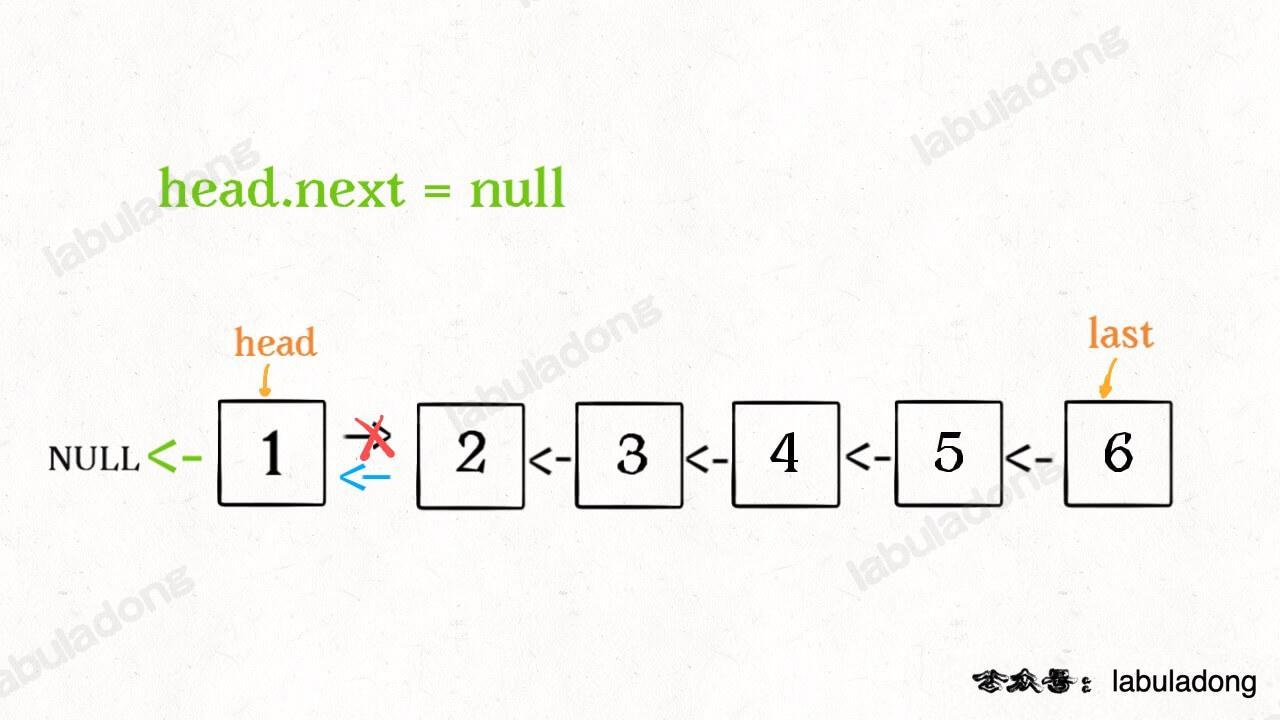
Amazing! Now the whole linked list is reversed. Recursive code is simple and elegant, but there are two things to pay attention to:
- The recursive function needs a base case, which is this line:
if (head == null || head.next == null) {
return head;
}This means if the list is empty or only has one node, the reversed result is itself, so just return it.
- After the list is reversed recursively, the new head is
last, and the oldheadbecomes the last node. Don't forget to set itsnextto null:
head.next = null;This way, the whole linked list is reversed. Isn’t it amazing? Here is a visual process of recursive reversal:
Algorithm Visualization
Do not get lost in recursion details
The visual panel can show all the steps of the recursion, but I do not suggest beginners focus too much on the details. First, use the way of thinking explained above to understand recursion, then use the visual panel to deepen your understanding.
Recursion is less efficient than iteration for linked lists
It is worth mentioning that recursion is not very efficient for linked lists.
The recursive and iterative solutions both have time complexity O(N), but the iterative one uses O(1) space, while the recursive one needs stack space, so its space complexity is O(N).
So, recursion is good for practicing thinking, but for efficiency, iteration is better.
Reverse the First N Nodes of a Linked List
Now let’s implement a function like this:
// Reverse the first n nodes of the linked list (n <= length of the list)
ListNode reverseN(ListNode head, int n)// Reverse the first n nodes of the linked list (n <= length of the list)
ListNode* reverseN(ListNode* head, int n);# Reverse the first n nodes of the linked list (n <= length of the list)
def reverseN(head: ListNode, n: int):// Reverse the first n nodes of the linked list (n <= length of the list)
func ReverseN(head *ListNode, n int) *ListNode {}// Reverse the first n nodes of the linked list (n <= length of the linked list)
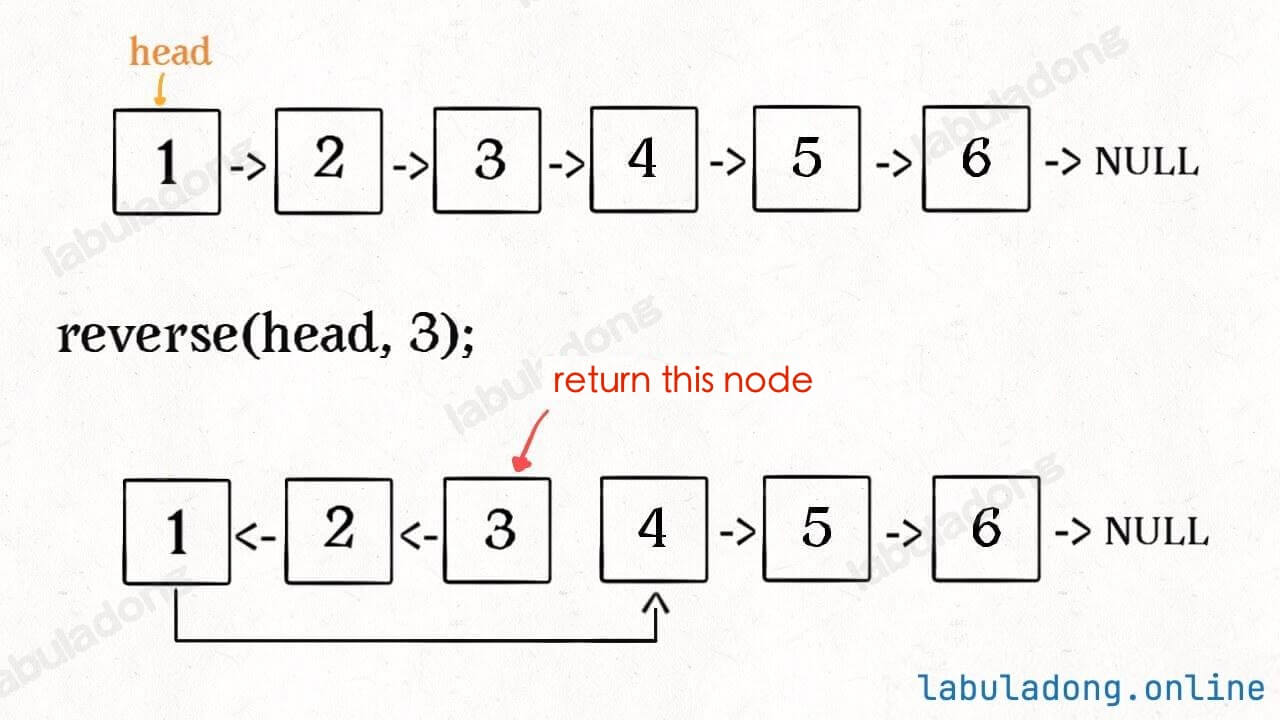
var reverseN = function(head, n) {}For example, for the linked list below, if you run reverseN(head, 3):