Prefix Sum Array Technique

The prefix sum technique is useful for quickly and frequently calculating the sum of elements within a range of indices.

Prefix Sum in One-Dimensional Arrays

Let's look at an example problem: LeetCode Problem 303 "Range Sum Query - Immutable". It requires calculating the sum of elements within a specified range of an array, which is a standard prefix sum problem:

Input
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
Output
[null, 1, -1, -3]

Explanation
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3

// The problem requires you to implement such a class
class NumArray {

    public NumArray(int[] nums) {}
    
    // Query the cumulative sum of the closed interval [left, right]
    public int sumRange(int left, int right) {}
}

// The problem requires you to implement such a class
class NumArray {
public:
    NumArray(vector<int>& nums) {}
    
    // Query the accumulated sum of the closed interval [left, right]
    int sumRange(int left, int right) {}
};

# The problem requires you to implement such a class
class NumArray:
    
    def __init__(self, nums: List[int]):
        pass
        
    # Query the accumulated sum of the closed interval [left, right]
    def sumRange(self, left: int, right: int) -> int:
        pass

// The problem requires you to implement such a class
type NumArray struct {}

func Constructor(nums []int) NumArray {}

// Query the cumulative sum of the closed interval [left, right]
func (this *NumArray) SumRange(left int, right int) int {}

// The problem requires you to implement such a class
var NumArray = function(nums) {
  
  this.nums = nums;
  
  // Query the accumulated sum of the closed interval [left, right]
  this.sumRange = function(left, right) {}
  
};

The sumRange function needs to calculate and return the sum of elements within a given index range. People who haven't learned about prefix sums might write code like this:

class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    public int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
}

class NumArray {
    
private:
    vector<int> nums;

public:
    NumArray(vector<int>& nums) {
        this->nums = nums;
    }
    
    int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
};

class NumArray:
    def __init__(self, nums: List[int]):
        self.nums = nums
    
    def sumRange(self, left: int, right: int) -> int:
        res = 0
        for i in range(left, right+1):
            res += self.nums[i]
        return res

type NumArray struct {
    nums []int
}

func Constructor(nums []int) NumArray {
    return NumArray{nums: nums}
}

func (this *NumArray) SumRange(left int, right int) int {
    res := 0
    for i := left; i <= right; i++{
        res += this.nums[i]
    }
    return res
}

var NumArray = function(nums) {
    this.nums = nums;
}

NumArray.prototype.sumRange = function(left, right) {
    let res = 0;
    for (let i = left; i <= right; i++) {
        res += this.nums[i];
    }
    return res;
}

This method can achieve the desired effect, but it is very inefficient because the sumRange method is frequently called, and its worst-case time complexity is $O(N)$, where N represents the length of the nums array.

The optimal solution to this problem is to use the prefix sum technique, which reduces the time complexity of the sumRange function to $O(1)$. Simply put, do not use a for loop within sumRange. How do we achieve this?

Let's look directly at the code implementation:

class NumArray {
    // prefix sum array
    private int[] preSum;

    // input an array to construct the prefix sum
    public NumArray(int[] nums) {
        // preSum[0] = 0, convenient for calculating the cumulative sum
        preSum = new int[nums.length + 1];
        // calculate the cumulative sum of nums
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    // query the cumulative sum of the closed interval [left, right]
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

class NumArray {
private:
    // prefix sum array
    vector<int> preSum;

public:
    // input an array, construct the prefix sum
    NumArray(vector<int>& nums) {
        // preSum[0] = 0, for easy calculation of cumulative sum
        preSum.resize(nums.size() + 1);
        // calculate the cumulative sum of nums
        for (int i = 1; i < preSum.size(); i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    // query the cumulative sum of the closed interval [left, right]
    int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
};

class NumArray:
    def __init__(self, nums: List[int]):
        # prefix sum array
        self.preSum = [0] * (len(nums) + 1)
        # calculate the cumulative sum of nums
        for i in range(1, len(self.preSum)):
            self.preSum[i] = self.preSum[i - 1] + nums[i - 1]

    def sumRange(self, left: int, right: int) -> int:
        # query the cumulative sum of the closed interval [left, right]
        return self.preSum[right + 1] - self.preSum[left]

type NumArray struct {
    // prefix sum array
    preSum []int
}

// input an array, construct the prefix sum
func Constructor(nums []int) NumArray {
    // preSum[0] = 0, for ease of calculating cumulative sum
    n := len(nums)
    preSum := make([]int, n + 1)
    // calculate the cumulative sum of nums
    for i := 1; i < n + 1; i++ {
        preSum[i] = preSum[i - 1] + nums[i - 1]
    }

    return NumArray{preSum: preSum}
}

// query the cumulative sum of the closed interval [left, right]
func (this *NumArray) SumRange(left int, right int) int {
    return this.preSum[right + 1] - this.preSum[left]
}

var NumArray = function(nums) {
    // prefix sum array
    this.preSum = new Array(nums.length + 1);
    
    // calculate the cumulative sum of nums
    this.preSum[0] = 0;
    for (let i = 1; i < this.preSum.length; i++) {
        this.preSum[i] = this.preSum[i - 1] + nums[i - 1];
    }
};

// query the cumulative sum of the closed interval [left, right]
NumArray.prototype.sumRange = function(left, right) {
    return this.preSum[right + 1] - this.preSum[left];
};

The core idea is to create a new array called preSum, where preSum[i] records the cumulative sum of nums[0..i-1]. For example, in the illustration, 10 = 3 + 5 + 2:

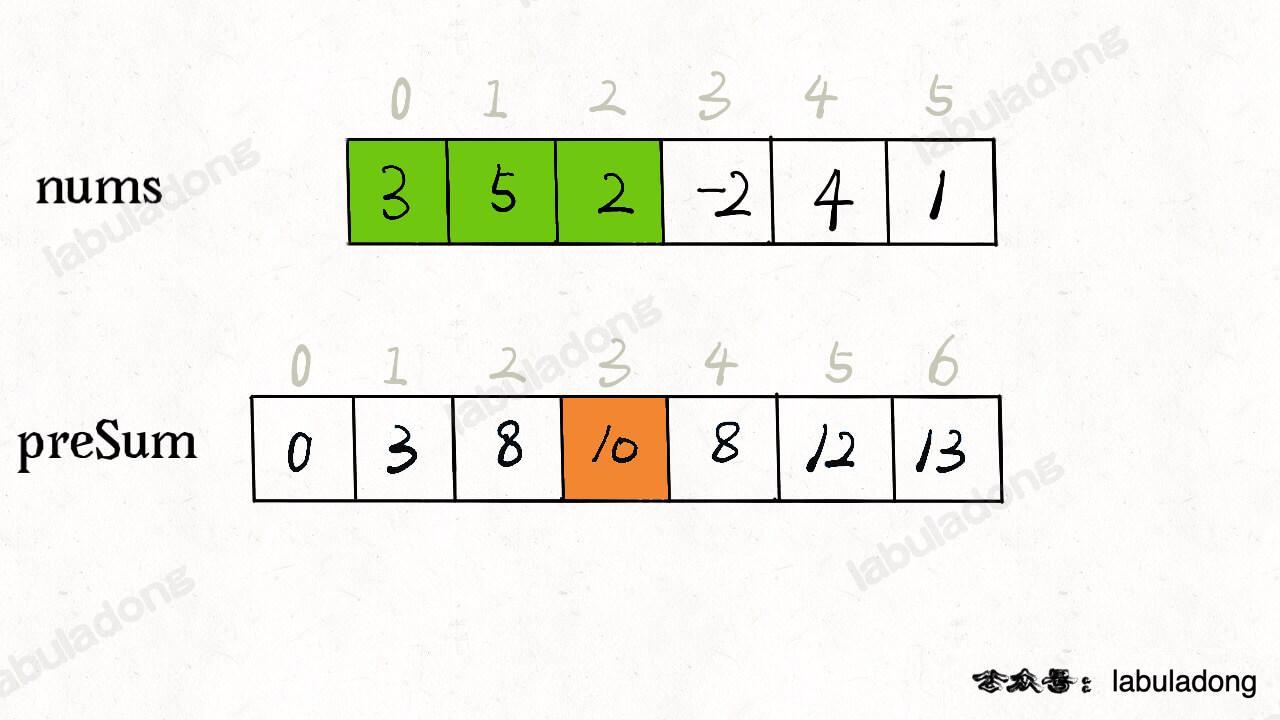
Consider this preSum array: if you want to find the sum of all elements within the index range [1, 4], you can simply compute it using preSum[5] - preSum[1].

In this way, the sumRange function only requires a single subtraction operation, avoiding the need for a for loop each time, resulting in a worst-case time complexity of constant $O(1)$.

This technique is also widely used in real life. For example, if your class has several students, each with a final exam score (out of 100), you could implement an API that, given any range of scores, returns how many students have scores within that range.

To achieve this, you can first use counting sort to calculate the number of students for each specific score, and then employ the prefix sum technique to implement the score range query API:

// stores all the students' scores
int[] scores;
// the full mark of the test paper is 100 points
int[] count = new int[100 + 1];
// record how many students have each score
for (int score : scores)
    count[score]++;
// construct the prefix sum
for (int i = 1; i < count.length; i++)
    count[i] = count[i] + count[i-1];
// use the prefix sum array 'count' to query score segments

Next, let's look at how the prefix sum concept is applied in a two-dimensional array.

Prefix Sum in a 2D Matrix

This is LeetCode problem 304 "Range Sum Query 2D - Immutable". It is similar to the previous problem, where you needed to calculate the sum of elements in a subarray. In this problem, you are asked to calculate the sum of elements in a submatrix of a 2D matrix:

304. Range Sum Query 2D - Immutable | LeetCode |

Given a 2D matrix matrix, handle multiple queries of the following type:

• Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

• NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
• int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

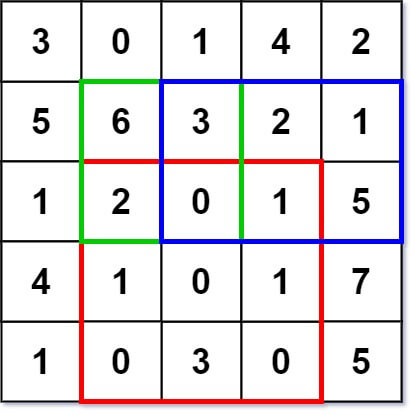
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -104 <= matrix[i][j] <= 104
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• At most 104 calls will be made to sumRegion.

Of course, you could use a nested for loop to traverse the matrix, but that would result in a higher time complexity for the sumRegion function, reducing the efficiency of your algorithm.

Notice that the sum of the elements in any submatrix can be converted into operations involving the sums of a few larger matrices:

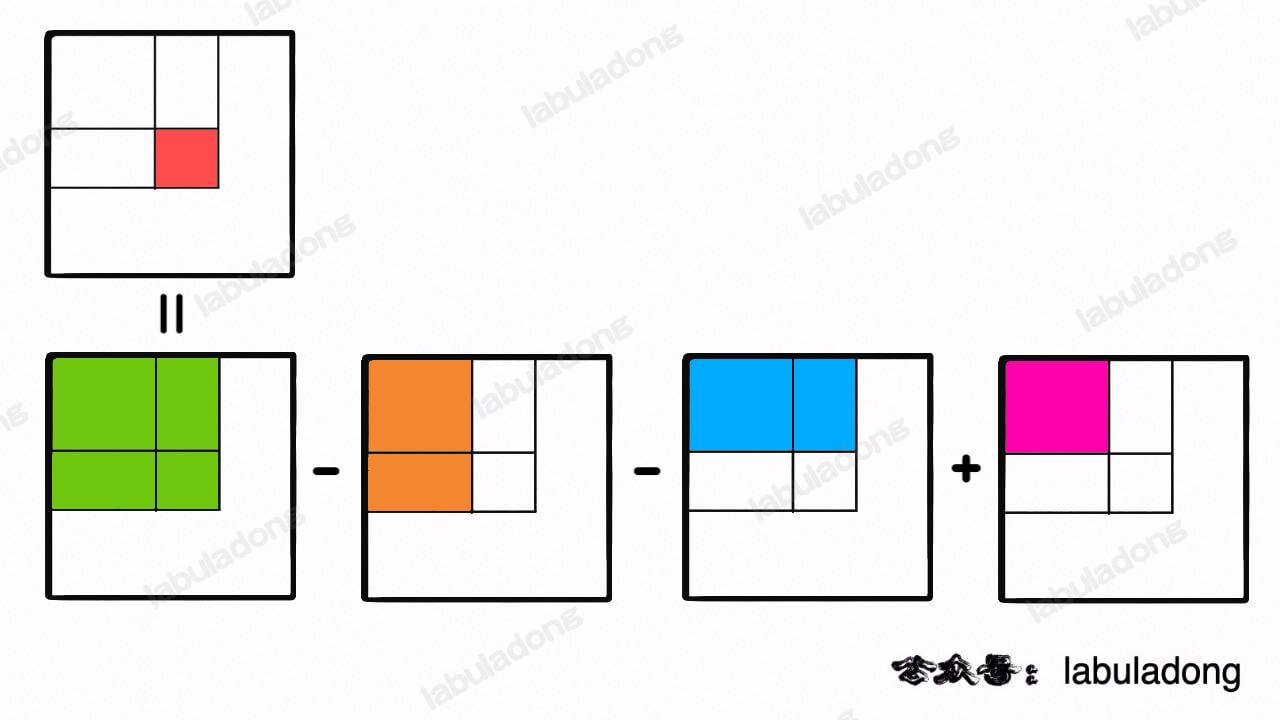
These four larger matrices share a common characteristic: their top-left corner is the origin (0, 0).

A better approach to this problem, similar to the prefix sum in a one-dimensional array, is to maintain a two-dimensional preSum array. This array records the sum of elements in matrices with the origin as the top-left vertex, allowing you to calculate the sum of any submatrix using a few addition and subtraction operations:

class NumMatrix {
    // definition: preSum[i][j] records the sum of
    // elements in the submatrix [0, 0, i-1, j-1] of
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        if (m == 0 || n == 0) return;
        // construct the prefix sum matrix
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // calculate the sum of elements for each matrix [0, 0, i, j]
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // calculate the sum of elements in the submatrix [x1, y1, x2, y2]
    public int sumRegion(int x1, int y1, int x2, int y2) {
        // the sum of the target matrix is obtained by operating the four adjacent matrices
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
}

class NumMatrix {
private:
    // definition: preSum[i][j] records the sum of
    // elements in the submatrix [0, 0, i-1, j-1] of
    vector<vector<int>> preSum;
    
public:
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        if (m == 0 || n == 0) return;
        // construct the prefix sum matrix
        preSum = vector<vector<int>>(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // calculate the sum of elements for each matrix [0, 0, i, j]
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // calculate the sum of elements of submatrix [x1, y1, x2, y2]
    int sumRegion(int x1, int y1, int x2, int y2) {
        // the sum of the target matrix is obtained by operating four adjacent matrices
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
};

class NumMatrix:
    # definition: preSum[i][j] records the sum of
    # elements in the submatrix [0, 0, i-1, j-1] of
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        if m == 0 or n == 0: return
        # Construct the prefix sum matrix
        self.preSum = [[0 for _ in range(n+1)] for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                # Calculate the sum of elements for each matrix [0, 0, i, j]
                self.preSum[i][j] = self.preSum[i-1][j] + self.preSum[i][j-1] + matrix[i-1][j-1] - self.preSum[i-1][j-1]

    # Calculate the sum of elements in submatrix [x1, y1, x2, y2]
    def sumRegion(self, x1: int, y1: int, x2: int, y2: int) -> int:
        # The sum of the target matrix is obtained by operating on four adjacent matrices
        return self.preSum[x2+1][y2+1] - self.preSum[x1][y2+1] - self.preSum[x2+1][y1] + self.preSum[x1][y1]

type NumMatrix struct {
    // definition: preSum[i][j] records the sum of
    // elements in the submatrix [0, 0, i-1, j-1] of
    preSum [][]int
}

func Constructor(matrix [][]int) NumMatrix {
    m, n := len(matrix), len(matrix[0])
    if m == 0 || n == 0 {
        return NumMatrix{}
    }
    // construct the prefix sum matrix
    preSum := make([][]int, m+1)
    for i := 0; i <= m; i++ {
        preSum[i] = make([]int, n+1)
    }
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            // calculate the sum of elements for each matrix [0, 0, i, j]
            preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i-1][j-1] - preSum[i-1][j-1]
        }
    }
    return NumMatrix{preSum: preSum}
}
// calculate the sum of elements in submatrix [x1, y1, x2, y2]
func (this *NumMatrix) SumRegion(x1 int, y1 int, x2 int, y2 int) int {
    // the sum of the target matrix is obtained by operating on four adjacent matrices
    return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1]
}

var NumMatrix = function(matrix) {
    var m = matrix.length, n = matrix[0].length;
    if (m === 0 || n === 0) return;
    // construct the prefix sum matrix
    this.preSum = new Array(m + 1).fill(null).map(() => new Array(n + 1).fill(0));
    for (var i = 1; i <= m; i++) {
        for (var j = 1; j <= n; j++) {
            // calculate the sum of elements for each matrix [0, 0, i, j]
            this.preSum[i][j] = this.preSum[i-1][j] + this.preSum[i][j-1] + matrix[i - 1][j - 1] - this.preSum[i-1][j-1];
        }
    }
};

// calculate the sum of elements in submatrix [x1, y1, x2, y2]
NumMatrix.prototype.sumRegion = function(x1, y1, x2, y2) {
    // the sum of the target matrix is obtained by operating on four adjacent matrices
    return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1];
};

In this way, the time complexity of the sumRegion function is optimized to $O(1)$ using the prefix sum technique. This is a classic example of the "space for time" trade-off.

That's all for the prefix sum technique. It can be said that this algorithmic technique is simple for those who understand it, while challenging for those who do not. In practical applications, it is essential to develop flexible thinking to quickly identify prefix sum problems.

Besides the basic usage examples provided in this article, prefix sum arrays are often combined with other data structures or algorithmic techniques. I will provide further examples and explanations in High-Frequency Prefix Sum Problems.