Monotonic Stack Code Template
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 496. Next Greater Element I | 🟢 |
| 503. Next Greater Element II | 🟠 |
| 739. Daily Temperatures | 🟠 |
Prerequisites
Before reading this article, you need to learn:
A stack is a simple data structure that follows a last-in-first-out order, which suits certain problems like function call stacks. A monotonic stack is essentially a stack that uses clever logic to maintain its elements in order (either non-decreasing or non-increasing) after each new element is pushed.
Does it sound like a heap? It's not. A monotonic stack is not widely used and mainly addresses specific problems like "next greater element" and "previous smaller element." This article explains the monotonic stack template to solve problems related to the "next greater element" and explores strategies for handling "circular arrays." Other variations and classic problems will be discussed in the next article Monotonic Stack Variations and Classic Exercises.
Monotonic Stack Template
Here is a problem for you: Given an array nums, return an array of the same length where each index stores the next greater element. If there is no greater element, store -1. The function signature is as follows:
int[] calculateGreaterElement(int[] nums);vector<int> calculateGreaterElement(vector<int>& nums);def calculateGreaterElement(nums: List[int])func calculateGreaterElement(nums []int) []intvar calculateGreaterElement = function(nums) {}For example, given an array nums = [2,1,2,4,3], you should return the array [4,2,4,-1,-1]. This is because the first 2 is followed by 4, which is greater than 2; 1 is followed by 2, which is greater than 1; the second 2 is followed by 4, which is greater than 2; after 4, there is no number greater than 4, so we fill in -1; after 3, there is no number greater than 3, so we fill in -1.
The brute-force solution to this problem is straightforward: for each element, scan the subsequent elements to find the first greater element. However, the time complexity of the brute-force solution is .
This problem can be abstracted as follows: imagine the elements of the array as people standing in a line, with their values representing their heights. These people are facing you, standing in a row. How do you find the next greater element for the element "2"? It's simple—if you can see the element "2", the first visible person behind it is the next greater element because shorter elements are blocked by "2". The first one to appear is the answer.
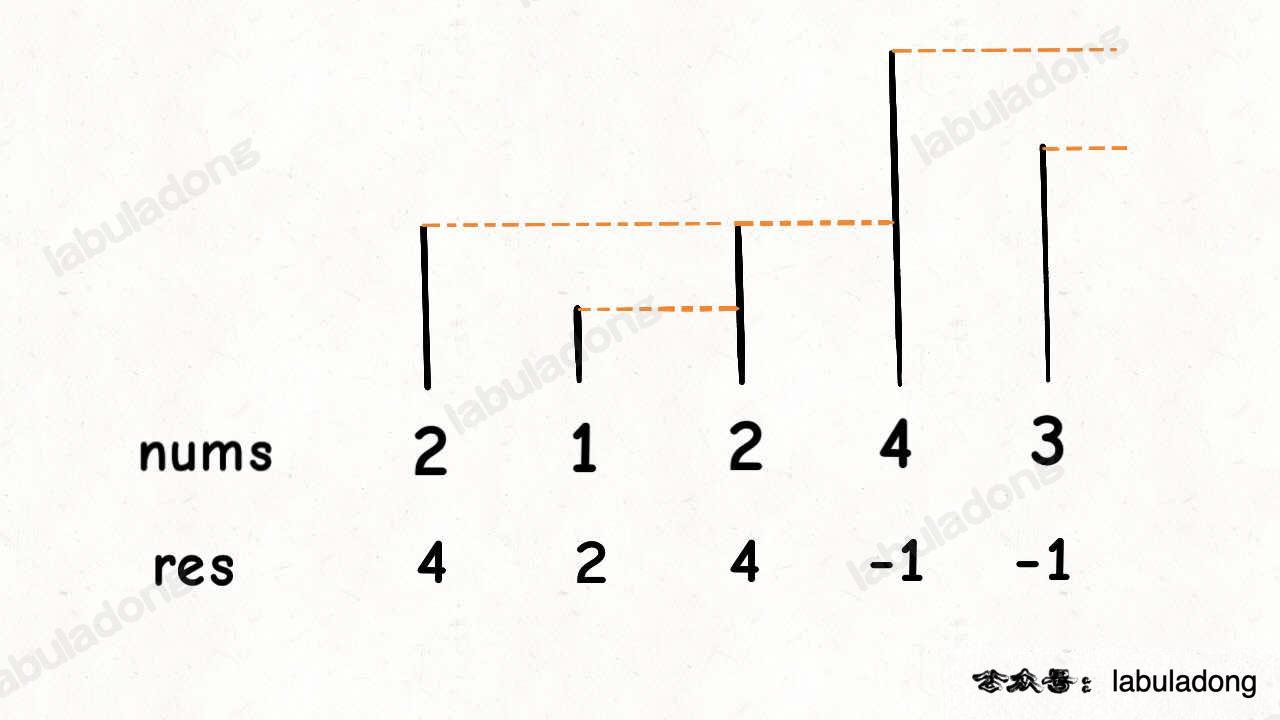
This scenario is easy to understand, right? With this abstract scenario in mind, let's look at the code.
int[] calculateGreaterElement(int[] nums) {
int n = nums.length;
// array to store the answers
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// push elements into the stack from the end
for (int i = n - 1; i >= 0; i--) {
// compare the heights
while (!s.isEmpty() && s.peek() <= nums[i]) {
// shorter ones step aside, they're blocked anyway...
s.pop();
}
// the greater element behind nums[i]
res[i] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i]);
}
return res;
}vector<int> calculateGreaterElement(vector<int>& nums) {
int n = nums.size();
// array to store the answer
vector<int> res(n);
stack<int> s;
// push elements into the stack in reverse order
for (int i = n - 1; i >= 0; i--) {
// compare the heights
while (!s.empty() && s.top() <= nums[i]) {
// shorter ones step aside, they're blocked anyway...
s.pop();
}
// the greater element behind nums[i]
res[i] = s.empty() ? -1 : s.top();
s.push(nums[i]);
}
return res;
}def calculateGreaterElement(nums):
n = len(nums)
# array to store the answers
res = [0]*n
s = []
# push elements into the stack backwards
for i in range(n-1, -1, -1):
# compare the heights
while s and s[-1] <= nums[i]:
# shorter ones step aside, they're blocked anyway...
s.pop()
# the greater element behind nums[i]
res[i] = -1 if not s else s[-1]
s.append(nums[i])
return resfunc calculateGreaterElement(nums []int) []int {
n := len(nums)
// array to store the answers
res := make([]int, n)
s := make([]int, 0)
// push elements into the stack from the end
for i := n - 1; i >= 0; i-- {
// compare the heights
for len(s) != 0 && s[len(s) - 1] <= nums[i] {
// remove shorter ones, they're blocked anyway...
s = s[:len(s)-1]
}
// the greater element behind nums[i]
if len(s) == 0 {
res[i] = -1
} else {
res[i] = s[len(s) - 1]
}
s = append(s, nums[i])
}
return res
}var calculateGreaterElement = function(nums) {
var n = nums.length;
// array to store the answers
var res = new Array(n);
var s = [];
// putting elements into the stack in reverse order
for (var i = n - 1; i >= 0; i--) {
// comparing heights
while (s.length != 0 && s[s.length-1] <= nums[i]) {
// shorter ones step aside, they're blocked anyway...
s.pop();
}
// the greater element behind nums[i]
res[i] = s.length == 0 ? -1 : s[s.length-1];
s.push(nums[i]);
}
return res;
}This is the template for solving problems using a monotonic stack. The for loop scans elements from back to front because we leverage the stack structure: pushing in reverse order results in popping in forward order. The while loop eliminates elements between two "taller" elements since their presence is insignificant; a "taller" element in front blocks them, making them impossible to be the next greater element for any subsequent element.
The time complexity of this algorithm is not immediately apparent. If you see a for loop nested within a while loop, you might assume a complexity of , but in reality, the complexity is only .
To analyze its time complexity, consider the process as a whole: there are n elements, each is pushed into the stack once and at most popped once, with no redundant operations. Hence, the total computational scale is proportional to the element scale n, which is a complexity of .
Problem Variations
The implementation of a monotonic stack is quite simple. Let's look at some specific problems.
496. Next Greater Element I
Let's start with a simple variation, LeetCode Problem 496 "Next Greater Element I":
496. Next Greater Element I | LeetCode | 🟢
The next greater element of some element x in an array is the first greater element that is to the right of x in the same array.
You are given two distinct 0-indexed integer arrays nums1 and nums2, where nums1 is a subset of nums2.
For each 0 <= i < nums1.length, find the index j such that nums1[i] == nums2[j] and determine the next greater element of nums2[j] in nums2. If there is no next greater element, then the answer for this query is -1.
Return an array ans of length nums1.length such that ans[i] is the next greater element as described above.
Example 1:
Input: nums1 = [4,1,2], nums2 = [1,3,4,2] Output: [-1,3,-1] Explanation: The next greater element for each value of nums1 is as follows: - 4 is underlined in nums2 = [1,3,4,2]. There is no next greater element, so the answer is -1. - 1 is underlined in nums2 = [1,3,4,2]. The next greater element is 3. - 2 is underlined in nums2 = [1,3,4,2]. There is no next greater element, so the answer is -1.
Example 2:
Input: nums1 = [2,4], nums2 = [1,2,3,4] Output: [3,-1] Explanation: The next greater element for each value of nums1 is as follows: - 2 is underlined in nums2 = [1,2,3,4]. The next greater element is 3. - 4 is underlined in nums2 = [1,2,3,4]. There is no next greater element, so the answer is -1.
Constraints:
1 <= nums1.length <= nums2.length <= 10000 <= nums1[i], nums2[i] <= 104- All integers in
nums1andnums2are unique. - All the integers of
nums1also appear innums2.
O(nums1.length + nums2.length) solution?This problem gives you two arrays, nums1 and nums2, and asks you to find the next greater element of each element in nums1 within nums2. The function signature is as follows:
int[] nextGreaterElement(int[] nums1, int[] nums2);vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2);def nextGreaterElement(nums1: List[int], nums2: List[int]) -> List[int]:func nextGreaterElement(nums1 []int, nums2 []int) []intvar nextGreaterElement = function(nums1, nums2) {}In fact, we can solve this problem by modifying our previous code. Since the problem states that nums1 is a subset of nums2, we first calculate the next greater element for each element in nums2 and store it in a mapping. Then, we simply look up the elements of nums1 in this mapping:
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
// record the next greater element for each element in nums2
int[] greater = nextGreaterElement(nums2);
// convert to a map: element x -> next greater element of x
HashMap<Integer, Integer> greaterMap = new HashMap<>();
for (int i = 0; i < nums2.length; i++) {
greaterMap.put(nums2[i], greater[i]);
}
// nums1 is a subset of nums2, so we can get the result based on greaterMap
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
res[i] = greaterMap.get(nums1[i]);
}
return res;
}
// calculate the next greater element for each element in nums
int[] nextGreaterElement(int[] nums) {
int n = nums.length;
// array to store the answers
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// push elements onto the stack in reverse order
for (int i = n - 1; i >= 0; i--) {
// determine the height (size) of elements
while (!s.isEmpty() && s.peek() <= nums[i]) {
// remove the shorter elements as they are blocked anyway
s.pop();
}
// the next greater element after nums[i]
res[i] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i]);
}
return res;
}
}#include <vector>
#include <stack>
#include <unordered_map>
class Solution {
public:
std::vector<int> nextGreaterElement(std::vector<int>& nums1, std::vector<int>& nums2) {
// record the next greater element for each element in nums2
std::vector<int> greater = nextGreaterElement(nums2);
// convert to a map: element x -> next greater element of x
std::unordered_map<int, int> greaterMap;
for (int i = 0; i < nums2.size(); i++) {
greaterMap[nums2[i]] = greater[i];
}
// nums1 is a subset of nums2, so we can get the result based on greaterMap
std::vector<int> res(nums1.size());
for (int i = 0; i < nums1.size(); i++) {
res[i] = greaterMap[nums1[i]];
}
return res;
}
// calculate the next greater element for each element in nums
std::vector<int> nextGreaterElement(std::vector<int>& nums) {
int n = nums.size();
// array to store the answers
std::vector<int> res(n);
std::stack<int> s;
// push elements onto the stack in reverse order
for (int i = n - 1; i >= 0; i--) {
// determine the height (size) of elements
while (!s.empty() && s.top() <= nums[i]) {
// remove the shorter elements as they are blocked anyway
s.pop();
}
// the next greater element after nums[i]
res[i] = s.empty() ? -1 : s.top();
s.push(nums[i]);
}
return res;
}
};class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
# record the next greater element for each element in nums2
greater = self.nextGreaterElementInternal(nums2)
# convert to a map: element x -> next greater element of x
greater_map = {}
for i in range(len(nums2)):
greater_map[nums2[i]] = greater[i]
# nums1 is a subset of nums2, so we can get the result based on greaterMap
res = [greater_map[num] for num in nums1]
return res
# calculate the next greater element for each element in nums
def nextGreaterElementInternal(self, nums: List[int]) -> List[int]:
n = len(nums)
# array to store the answers
res = [-1] * n # Initialize with -1 as specified in the problem statement
stack = []
# push elements onto the stack in reverse order
for i in range(n - 1, -1, -1):
# determine the height (size) of elements
while stack and stack[-1] <= nums[i]:
# remove the shorter elements as they are blocked anyway
stack.pop()
# the next greater element after nums[i]
res[i] = stack[-1] if stack else -1
stack.append(nums[i])
return resfunc nextGreaterElement(nums1 []int, nums2 []int) []int {
// record the next greater element for each element in nums2
greater := nextGreaterElementSingle(nums2)
// convert to a map: element x -> next greater element of x
greaterMap := make(map[int]int)
for i, num := range nums2 {
greaterMap[num] = greater[i]
}
// nums1 is a subset of nums2, so we can get the result based on greaterMap
res := make([]int, len(nums1))
for i, num := range nums1 {
res[i] = greaterMap[num]
}
return res
}
// calculate the next greater element for each element in nums
func nextGreaterElementSingle(nums []int) []int {
n := len(nums)
// array to store the answers
res := make([]int, n)
stack := []int{}
// push elements onto the stack in reverse order
for i := n - 1; i >= 0; i-- {
// determine the height (size) of elements
for len(stack) > 0 && stack[len(stack)-1] <= nums[i] {
// remove the shorter elements as they are blocked anyway
stack = stack[:len(stack)-1]
}
// the next greater element after nums[i]
if len(stack) == 0 {
res[i] = -1
} else {
res[i] = stack[len(stack)-1]
}
stack = append(stack, nums[i])
}
return res
}var nextGreaterElement = function(nums1, nums2) {
// record the next greater element for each element in nums2
let greater = calculateNextGreaterElement(nums2);
// convert to a map: element x -> next greater element of x
let greaterMap = new Map();
for (let i = 0; i < nums2.length; i++) {
greaterMap.set(nums2[i], greater[i]);
}
// nums1 is a subset of nums2, so we can get the result based on greaterMap
let res = new Array(nums1.length);
for (let i = 0; i < nums1.length; i++) {
res[i] = greaterMap.get(nums1[i]);
}
return res;
};
// calculate the next greater element for each element in nums
var calculateNextGreaterElement = function(nums) {
let n = nums.length;
// array to store the answers
let res = new Array(n);
let s = [];
// push elements onto the stack in reverse order
for (let i = n - 1; i >= 0; i--) {
// determine the height (size) of elements
while (s.length > 0 && s[s.length - 1] <= nums[i]) {
// remove the shorter elements as they are blocked anyway
s.pop();
}
// the next greater element after nums[i]
res[i] = s.length === 0 ? -1 : s[s.length - 1];
s.push(nums[i]);
}
return res;
};Algorithm Visualization
739. Daily Temperatures
Let's look at LeetCode problem 739, "Daily Temperatures":
You are given an array temperatures that represents the daily temperatures. Return an array of the same length where each element represents the number of days you have to wait until a warmer temperature. If there is no future day with a warmer temperature, fill it with 0. The function signature is as follows:
int[] dailyTemperatures(int[] temperatures);vector<int> dailyTemperatures(vector<int>& temperatures);def dailyTemperatures(temperatures: List[int]) -> List[int]:func dailyTemperatures(temperatures []int) []intvar dailyTemperatures = function(temperatures) {}For example, if you are given the input temperatures = [73,74,75,71,69,76], you should return [1,1,3,2,1,0]. This is because on the first day, the temperature is 73°F, and on the second day, it is 74°F, which is higher than 73°F. So, for the first day, you only need to wait one day to get a warmer temperature. The same logic applies to the subsequent days.
Essentially, this problem is about finding the next greater element. However, instead of asking for the value of the next greater element, it asks for the index distance from the current element to the next greater element.
Using the same approach, you can directly apply the monotonic stack algorithm template with slight modifications. Here is the code:
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length;
int[] res = new int[n];
// Store element indices here, not the elements themselves
Stack<Integer> s = new Stack<>();
// Monotonic stack template
for (int i = n - 1; i >= 0; i--) {
while (!s.isEmpty() && temperatures[s.peek()] <= temperatures[i]) {
s.pop();
}
// Get the distance between indices
res[i] = s.isEmpty() ? 0 : (s.peek() - i);
// Push the index onto the stack, not the element
s.push(i);
}
return res;
}
}class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> res(n, 0);
// Store element indices here, not elements
stack<int> s;
// Monotonic stack template
for (int i = n - 1; i >= 0; i--) {
while (!s.empty() && temperatures[s.top()] <= temperatures[i]) {
s.pop();
}
// Get the distance between indices
res[i] = s.empty() ? 0 : (s.top() - i);
// Push the index onto the stack, not the element
s.push(i);
}
return res;
}
};class Solution:
def dailyTemperatures(self, temperatures):
n = len(temperatures)
res = [0]*n
# Store element indices here, not elements
s = []
# Monotonic stack template
for i in range(n-1, -1, -1):
while s and temperatures[s[-1]] <= temperatures[i]:
s.pop()
# Get the index difference
res[i] = 0 if not s else s[-1] - i
# Push the index onto the stack, not the element
s.append(i)
return resfunc dailyTemperatures(temperatures []int) []int {
n := len(temperatures)
res := make([]int, n)
s := make([]int, 0)
// monotonic stack template
for i := n - 1; i >= 0; i-- {
for len(s) > 0 && temperatures[s[len(s)-1]] <= temperatures[i] {
s = s[:len(s)-1]
}
// get the index distance
if len(s) == 0 {
res[i] = 0
} else {
res[i] = s[len(s)-1] - i
}
// push the index onto the stack, not the element
s = append(s, i)
}
return res
}var dailyTemperatures = function(temperatures) {
let n = temperatures.length;
let res = new Array(n).fill(0);
// Store element indices here, not the elements themselves
let s = [];
// Monotonic stack template
for (let i = n - 1; i >= 0; i--) {
while (s.length > 0 && temperatures[s[s.length - 1]] <= temperatures[i]) {
s.pop();
}
// Get the distance between indices
res[i] = s.length === 0 ? 0 : (s[s.length - 1] - i);
// Push the index onto the stack, not the element
s.push(i);
}
return res;
};Now that we've covered monotonic stacks, let's move on to another key topic: how to handle circular arrays.
How to Handle Circular Arrays
Consider the problem of finding the next greater element, but now assume the array is circular. How should we approach this? LeetCode problem 503, "Next Greater Element II", addresses this: given a circular array, compute the next greater element for each element.
For example, given the input [2,1,2,4,3], you should return [4,2,4,-1,4]. Due to the circular nature, the last element 3 loops around and finds the greater element 4.
If you've read the Circular Array Techniques section in the basics chapter, you should be familiar with this. We typically use the modulo operator (%) to simulate the circular effect:
int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
// Rotate in a circular array
print(arr[index % n]);
index++;
}int main(){
int arr[5] = {1, 2, 3, 4, 5};
int n = sizeof(arr) / sizeof(arr[0]), index = 0;
while (true) {
// loop around in the circular array
cout << arr[index % n] << endl;
index++;
}
return 0;
}arr = [1,2,3,4,5]
n = len(arr)
index = 0
while True:
# Circulate in a circular array
print(arr[index % n])
index += 1arr := []int{1, 2, 3, 4, 5}
n := len(arr)
index := 0
for {
// Rotate in a circular array
fmt.Println(arr[index % n])
index++
}var arr = [1,2,3,4,5];
var n = arr.length, index = 0;
while (true) {
// Rotate in a circular array
console.log(arr[index % n]);
index++;
}This problem should definitely be approached using the monotonic stack template, but the challenge lies in finding the next greater element for the last element, like how to find element 4 as the next greater element for 3 when the input is [2,1,2,4,3].
The common technique for this requirement is to effectively double the length of the array:
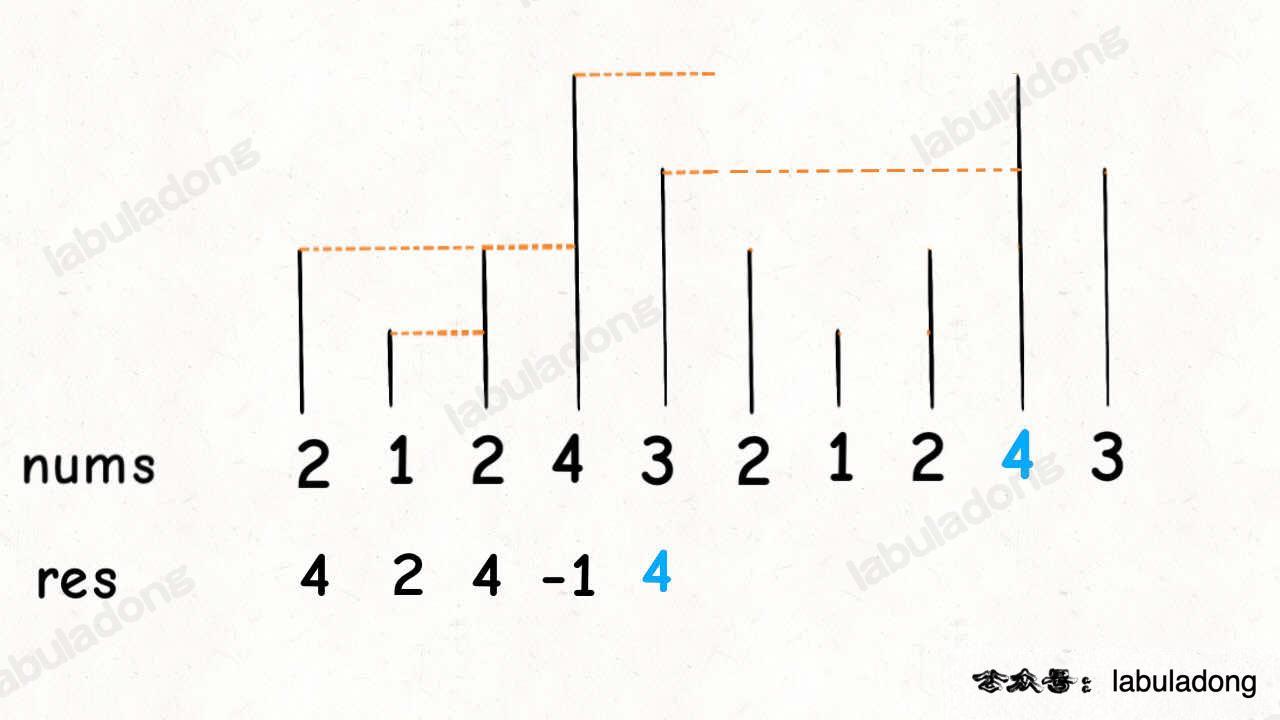
In doing so, element 3 can find element 4 as the next greater element, and all other elements can be correctly computed as well.
With this concept in mind, the simplest way to implement it is to construct this doubled-length array and apply the algorithm template. However, we can avoid creating a new array by using the technique of circular arrays to simulate the effect of doubling the array length. Let's take a look at the code directly:
class Solution {
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// Double the array length to simulate a circular array
for (int i = 2 * n - 1; i >= 0; i--) {
// Index i needs to be modulo, the rest is the same as the template
while (!s.isEmpty() && s.peek() <= nums[i % n]) {
s.pop();
}
res[i % n] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i % n]);
}
return res;
}
}class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
vector<int> res(n);
stack<int> s;
// Double the array length to simulate a circular array
for (int i = 2 * n - 1; i >= 0; i--) {
// Index i needs to be modulated, the rest is the same as the template
while (!s.empty() && s.top() <= nums[i % n]) {
s.pop();
}
res[i % n] = s.empty() ? -1 : s.top();
s.push(nums[i % n]);
}
return res;
}
};class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
n = len(nums)
res = [0] * n
# Use an array to simulate a stack
s = []
# Double the array length to simulate a circular array
for i in range(2 * n - 1, -1, -1):
# Index i needs to be modulo, the rest is the same as the template
while s and s[-1] <= nums[i % n]:
s.pop()
res[i % n] = -1 if not s else s[-1]
s.append(nums[i % n])
return resfunc nextGreaterElements(nums []int) []int {
n := len(nums)
res := make([]int, n)
// use an array to simulate a stack
s := make([]int, 0)
// double the array length to simulate a circular array
for i := 2 * n - 1; i >= 0; i-- {
// index i needs to be modulo, the rest is the same as the template
for len(s) > 0 && s[len(s)-1] <= nums[i % n] {
s = s[:len(s)-1] // pop element from stack
}
if len(s) == 0 {
res[i % n] = -1
} else {
res[i % n] = s[len(s) - 1]
}
s = append(s, nums[i % n]) // push element to stack
}
return res
}var nextGreaterElements = function(nums) {
let n = nums.length;
let res = new Array(n);
// use array to simulate a stack
let s = [];
// double the array length to simulate a circular array
for (let i = 2 * n - 1; i >= 0; i--) {
// index i needs modulo, the rest is the same as the template
while (s.length !== 0 && s[s.length - 1] <= nums[i % n]) {
s.pop();
}
res[i % n] = s.length === 0 ? -1 : s[s.length - 1];
s.push(nums[i % n]);
}
return res;
};Algorithm Visualization
This method can cleverly solve the problem of circular arrays with a time complexity of .
Finally, let's raise some questions. The monotonic stack template provided in this article is the nextGreaterElement function, which can calculate the next greater element for each element. But how should you modify the template if the problem asks you to calculate the previous greater element or the previous greater or equal element? In practical applications, problems won't directly ask you to calculate the next (or previous) greater (or smaller) element. How would you transform the problem into one related to monotonic stacks?
I will compare several other forms of monotonic stacks in Variants and Exercises of Monotonic Stacks and provide classic examples of monotonic stacks. For more data structure design problems, refer to Classic Exercises on Data Structure Design.