Monotonic Queue to Solve Sliding Window Problems

In a previous article Solving Three Algorithm Problems Using Monotonic Stack, we introduced the special data structure called monotonic stack. Here, we will discuss a similar data structure called "monotonic queue."

You might not have heard of this data structure before. Essentially, it is just a "queue" that uses a clever method to ensure that the elements in the queue are all monotonically increasing (or decreasing).

Why invent a structure like the "monotonic queue"? It is mainly to solve the following scenario:

Given an array window with a known extreme value A, if you add a number B to window, you can immediately calculate the new extreme value by comparing A and B. However, if you remove a number from window, you cannot directly obtain the extreme value. If the removed number happens to be A, you need to traverse all elements in window to find the new extreme value.

This scenario is common, but it seems that a monotonic queue is not necessary. For example, a priority queue (binary heap) is specifically designed for dynamically finding extreme values. By creating a max (min) heap, you can quickly get the maximum (minimum) value, right?

For simply maintaining the extreme values, a priority queue is professional, with the head of the queue being the extreme value. However, a priority queue cannot satisfy the standard "first-in, first-out" time sequence of a queue structure. This is because a priority queue uses a binary heap to dynamically sort elements, and the order of dequeue is determined by the element size, having no relation to the order of enqueue.

Thus, a new queue structure is needed that can both maintain the "first-in, first-out" time sequence of queue elements and correctly maintain the extreme values of all elements in the queue, which is the "monotonic queue" structure.

The "monotonic queue" is mainly used to assist in solving problems related to sliding windows. In the previous article Core Framework of Sliding Window, the sliding window algorithm is explained as a part of the double pointer technique. However, some slightly more complex sliding window problems cannot be solved with just two pointers and require more advanced data structures.

For instance, in the previous article Core Framework of Sliding Window, for each problem discussed, whenever the window is expanded (right++) or contracted (left++), you can decide whether to update the answer based solely on the elements entering and leaving the window.

But in the example at the beginning of this article about determining the extreme value in a window, you cannot update the extreme value of the window based solely on the element leaving the window, unless you traverse all elements again, which increases the time complexity, something we do not want to see.

Let's look at LeetCode Problem 239 Sliding Window Maximum, which is a standard sliding window problem:

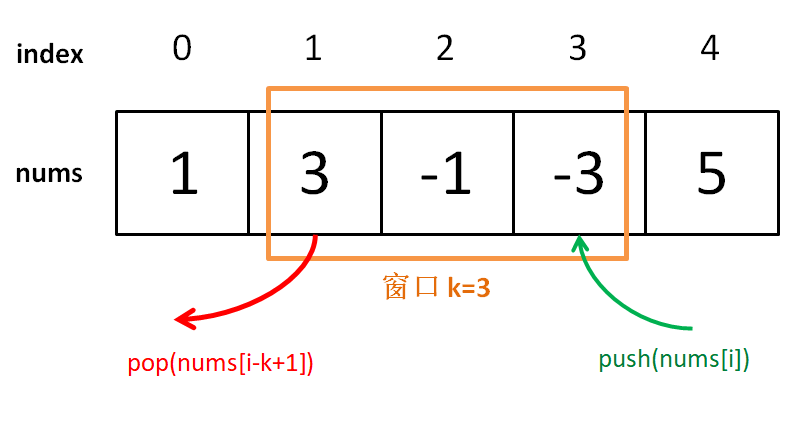
Given an array nums and a positive integer k, there is a window of size k that slides from left to right across nums. Please output the maximum value of k elements in the window each time.

The function signature is as follows:

int[] maxSlidingWindow(int[] nums, int k);

vector<int> maxSlidingWindow(vector<int>& nums, int k);

def maxSlidingWindow(nums: List[int], k: int) -> List[int]:

func maxSlidingWindow(nums []int, k int) []int

var maxSlidingWindow = function(nums, k)

For example, here is a sample problem provided by LeetCode:

Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
Output: [3,3,5,5,6,7]
Explanation:
Position of the sliding window          Maximum value
---------------                         -----
[1  3  -1] -3  5  3  6  7                3
 1 [3  -1  -3] 5  3  6  7                3
 1  3 [-1  -3  5] 3  6  7                5
 1  3  -1 [-3  5  3] 6  7                5
 1  3  -1  -3 [5  3  6] 7                6
 1  3  -1  -3  5 [3  6  7]               7

Next, we will use a monotonic queue structure to calculate the maximum value in each sliding window in $O(1)$ time, allowing the entire algorithm to be completed in linear time.

1. Building the Solution Framework

Before introducing the API of the "monotonic queue" data structure, let's compare the standard API of a regular queue with the API implemented by the monotonic queue:

// API for a regular queue
class Queue {
    // enqueue operation, add element n to the end of the queue
    void push(int n);
    // dequeue operation, remove the front element of the queue
    void pop();
}

// API for a monotonic queue
class MonotonicQueue {
    // add element n to the end of the queue
    void push(int n);
    // return the maximum value currently in the queue
    int max();
    // if the front element is n, remove it
    void pop(int n);
}

// API for a regular queue
class Queue {
public:
    // enqueue operation, add element n to the end of the queue
    void push(int n);
    // dequeue operation, remove element from the front of the queue
    void pop();
};

// API for a monotonic queue
class MonotonicQueue {
public:
    // add element n to the end of the queue
    void push(int n);
    // return the maximum value in the current queue
    int max();
    // remove the front element if it is n
    void pop(int n);
};

# API for a regular queue
class Queue:
    # enqueue operation, add element n to the end of the queue
    def push(self, n: int):
        pass
    
    # dequeue operation, remove the front element of the queue
    def pop(self):
        pass

# API for a monotonic queue
class MonotonicQueue:
    # add element n to the end of the queue
    def push(self, n: int):
        pass

    # return the maximum value in the current queue
    def max(self) -> int:
        pass

    # if the front element is n, remove it
    def pop(self, n: int):
        pass

// API of a regular queue
type Queue struct{}

// push operation, add element n to the end of the queue
func (q *Queue) push(n int) {}

// pop operation, remove the element at the front of the queue
func (q *Queue) pop() {}


// API of a monotonic queue
type MonotonicQueue struct{}

// add element n to the end of the queue
func (q *MonotonicQueue) push(n int) {}

// return the maximum value in the current queue
func (q *MonotonicQueue) max() int {}

// API for a regular queue
class Queue {
    // enqueue operation, add element n to the tail of the queue
    push(n) {}

    // dequeue operation, remove the head element of the queue
    pop() {}
};

// API for a monotonic queue
class MonotonicQueue {
    // add element n to the tail of the queue
    push(n) {}

    // return the maximum value in the current queue
    max() {}

    // if the head element is n, remove it
    pop(n) {}
};

Of course, the implementation of these APIs for a monotonic queue is different from a regular Queue, but for now, let's assume these operations have a time complexity of O(1) and first set up the solution framework for this "sliding window" problem:

int[] maxSlidingWindow(int[] nums, int k) {
    MonotonicQueue window = new MonotonicQueue();
    List<Integer> res = new ArrayList<>();
    
    for (int i = 0; i < nums.length; i++) {
        if (i < k - 1) {
            // first fill the window with the first k - 1 elements
            window.push(nums[i]);
        } else {
            // the window starts sliding forward
            // move in the new element
            window.push(nums[i]);
            // record the maximum element in the current window to the result
            res.add(window.max());
            // remove the last element
            window.pop(nums[i - k + 1]);
        }
    }
    // convert the List to an int[] array as the return value
    int[] arr = new int[res.size()];
    for (int i = 0; i < res.size(); i++) {
        arr[i] = res.get(i);
    }
    return arr;
}

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    MonotonicQueue window;
    vector<int> res;

    for (int i = 0; i < nums.size(); i++) {
        if (i < k - 1) {
            // first fill the window with the first k - 1 elements
            window.push(nums[i]);
        } else {
            // the window starts to slide forward
            // insert the new element
            window.push(nums[i]);
            // record the maximum element in the current window into the result
            res.push_back(window.max());
            // remove the last element
            window.pop(nums[i - k + 1]);
        }
    }
    return res;
}

from collections import deque
from typing import List

def maxSlidingWindow(nums: List[int], k: int) -> List[int]:
    window = MonotonicQueue()
    res = []

    for i in range(len(nums)):
        if i < k - 1:
            # first fill the window with the first k - 1 elements
            window.append(nums[i])
        else:
            # the window starts to slide forward
            # insert the new element
            window.append(nums[i])
            # add the maximum element of the current window to the result
            res.append(max(window))
            # remove the last element
            window.popleft()

    # convert the List type to an int[] array as the return value
    return res

func maxSlidingWindow(nums []int, k int) []int {
    window := MonotonicQueue{}
    var res []int

    for i:=0; i<len(nums); i++ {
        if i < k - 1 {
            // first fill the window with the first k-1 elements
            window.Push(nums[i])
        } else {
            // the window starts to slide forward
            // add new element
            window.Push(nums[i])
            // record the maximum element in the current window to the result
            res = append(res, window.Max())
            // remove the last element
            window.Pop(nums[i-k+1])
        }
    }
    return res
}

var maxSlidingWindow = function(nums, k) {
    var window = new MonotonicQueue();
    var res = [];
    
    for (var i = 0; i < nums.length; i++) {
        if (i < k - 1) {
            // first fill the window with the first k - 1 elements
            window.push(nums[i]);
        } else {
            // the window starts to slide forward
            // push new element
            window.push(nums[i]);
            // record the maximum element in the current window
            res.push(window.max());
            // pop the last element
            window.pop(nums[i - k + 1]);
        }
    }
    return res;
};

This idea is quite simple, right? Now let's start with the main part, the implementation of the monotonic queue.

2. Implementing the Monotonic Queue Data Structure

By observing the sliding window process, we can see that implementing a "monotonic queue" requires a data structure that supports insertion and deletion at both the head and tail. Clearly, a doubly linked list meets this requirement.

The core idea of the "monotonic queue" is similar to the "monotonic stack." The push method still adds elements at the queue's tail, but it removes elements in front that are smaller than itself:

class MonotonicQueue {
    // doubly linked list, supports quick insertion and deletion at both head and tail
    // maintain elements in a monotonically increasing order from tail to head
    private LinkedList<Integer> maxq = new LinkedList<>();

    // add an element n at the tail, maintaining the monotonic property of maxq
    public void push(int n) {
        // remove all elements smaller than itself from the front
        while (!maxq.isEmpty() && maxq.getLast() < n) {
            maxq.pollLast();
        }
        maxq.addLast(n);
    }
}

#include <list>
using namespace std;

class MonotonicQueue {
    // doubly linked list, supports fast insertions and deletions at both ends
    // maintain the elements in monotonically increasing order from tail to head
    list<int> maxq;

public:
    // add an element n at the tail, maintaining the monotonic property of maxq
    void push(int n) {
        // remove all elements smaller than itself from the front
        while (!maxq.empty() && maxq.back() < n) {
            maxq.pop_back();
        }
        maxq.push_back(n);
    }

};

from collections import deque

class MonotonicQueue:
    
    def __init__(self):
        # use a deque to support adding and removing elements from both ends
        # maintain the elements in increasing order from tail to head
        self.maxq = deque()
    
    # add an element n to the tail, maintaining the monotonic property of maxq
    def push(self, n: int) -> None:
        # remove all elements before it that are smaller than itself
        while len(self.maxq) > 0 and self.maxq[-1] < n:
            self.maxq.pop()
        self.maxq.append(n)

import (
	"container/list"
)

type MonotonicQueue struct {
    // use golang doubly linked list, supports adding and removing elements from head and tail
    // maintain elements in increasing order from tail to head
    maxq list.List
}

// add an element n to the tail, maintaining the monotonic property of mq
func (mq *MonotonicQueue) Push(n int) {
    // remove all elements in front that are smaller than itself
    for mq.maxq.Len() > 0 && mq.maxq.Back().Value.(int) < n {
        mq.maxq.Remove(mq.maxq.Back())
    }
}

class MonotonicQueue {

    constructor() {
        // JavaScript does not have a built-in data structure that
        // supports fast addition and removal of elements from both ends
        // Let's temporarily use a regular array, but this might
        // perform poorly when removing elements from the head
        // Maintain the elements in a monotonically increasing order from tail to head
        this.maxq = []
    }

    // Add an element n to the tail, maintaining the monotonic property of maxq
    push(n) {
        // Remove all elements smaller than itself from the front
        while (this.maxq.length > 0 && this.maxq[this.maxq.length - 1] < n) {
            this.maxq.pop()
        }
        this.maxq.push(n)
    }
}

Imagine that the size of a number represents a person's weight. A heavier weight will flatten the lighter ones in front of it until it encounters a weight of greater magnitude.

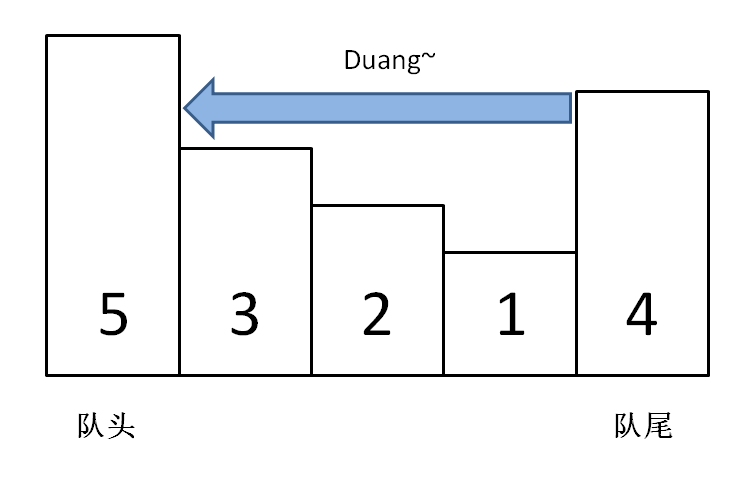
If each element is processed in this manner when added, the elements in the monotonic queue will maintain a monotonically decreasing order. This makes our max method straightforward to implement: simply return the front element of the queue. The pop method also operates on the front of the queue. If the front element is the element n to be removed, then delete it:

class MonotonicQueue {
    // to save space, the previous code section is omitted...

    public int max() {
        // the element at the front of the queue is definitely the largest
        return maxq.getFirst();
    }

    public void pop(int n) {
        if (n == maxq.getFirst()) {
            maxq.pollFirst();
        }
    }
}

class MonotonicQueue {
    // to save space, the code given above is omitted...

public:
    int max() {
        // the element at the front of the queue is definitely the largest
        return maxq.front();
    }

    void pop(int n) {
        if (n == maxq.front()) {
            maxq.pop_front();
        }
    }
};

class MonotonicQueue:
    # To save space, the previous code part is omitted...

    def max(self) -> int:
        # The element at the head of the queue is definitely the largest
        return self.maxq[0]

    def pop(self, n: int) -> None:
        if n == self.maxq[0]:
            self.maxq.popleft()

// to save space, the previous code part is omitted...

func (mq *MonotonicQueue) max() int {
    // the front element of the queue is surely the largest
    return mq.maxq.Front().Value.(int)
}

func (mq *MonotonicQueue) pop(n int) {
    if n == mq.maxq.Front().Value.(int) {
        mq.maxq.Remove(mq.maxq.Front())
    }
}

class MonotonicQueue {
    // in order to save space, the code above is omitted...

    max() {
        // the element at the head of the queue is definitely the largest
        return this.maxq[0];
    }

    pop(n) {
        if (n === this.maxq[0]) {
            this.maxq.shift();
        }
    }
}

The reason the pop method checks if n == maxq.getFirst() is that the front element n we want to remove might have been "flattened" during the push process and may no longer exist. In this case, we don't need to remove it:

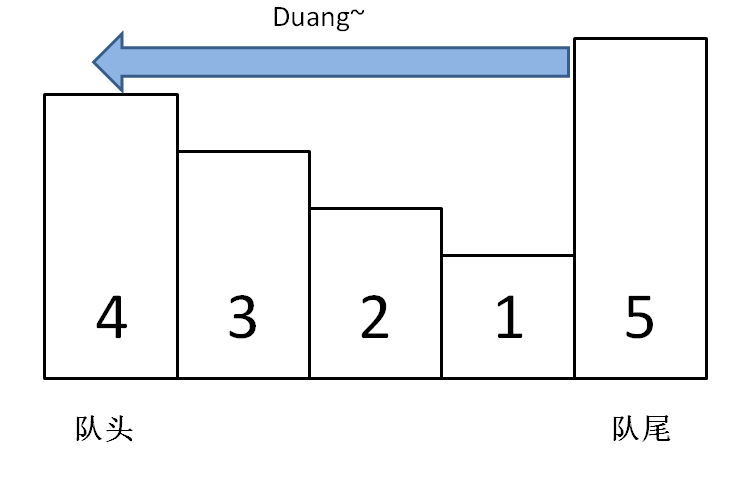
With this, the design of the monotonic queue is complete. Let's look at the full solution code:

class Solution {
    // implementation of the monotonic queue
    class MonotonicQueue {
        LinkedList<Integer> q = new LinkedList<>();
        public void push(int n) {
            // remove all elements smaller than n
            while (!q.isEmpty() && q.getLast() < n) {

                q.pollLast();
            }
            // then add n to the end
            q.addLast(n);
        }

        public int max() {
            return q.getFirst();
        }

        public void pop(int n) {
            if (n == q.getFirst()) {
                q.pollFirst();
            }
        }
    }

    // implementation of the solution function
    public int[] maxSlidingWindow(int[] nums, int k) {
        MonotonicQueue window = new MonotonicQueue();
        List<Integer> res = new ArrayList<>();

        for (int i = 0; i < nums.length; i++) {
            if (i < k - 1) {
                // first fill the window with the first k - 1 elements
                window.push(nums[i]);
            } else {

                // slide the window forward and add the new number
                window.push(nums[i]);
                // record the maximum value of the current window
                res.add(window.max());
                // remove the old number
                window.pop(nums[i - k + 1]);
            }
        }
        // need to convert to int[] array before returning
        int[] arr = new int[res.size()];
        for (int i = 0; i < res.size(); i++) {
            arr[i] = res.get(i);
        }
        return arr;
    }
}

// implementation of monotonic queue
class MonotonicQueue {
    deque<int> maxq;
public:
    void push(int n) {
        // remove all elements smaller than n
        while (!maxq.empty() && maxq.back() < n) {

            maxq.pop_back();
        }
        // then add n to the back
        maxq.push_back(n);
    }
    
    int max() {
        return maxq.front();
    }
    
    void pop(int n) {
        if (n == maxq.front()) {
            maxq.pop_front();
        }
    }
};

class Solution {
    public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        MonotonicQueue window;
        vector<int> res;
        
        for (int i = 0; i < nums.size(); i++) {
            if (i < k - 1) {
                // first fill the window with the first k - 1 elements
                window.push(nums[i]);
            } else {

                // slide the window forward and add a new number
                window.push(nums[i]);
                // record the max value of the current window
                res.push_back(window.max());
                // remove the old number
                window.pop(nums[i - k + 1]);
            }
        }
        return res;
    }
};

class MonotonicQueue:
    def __init__(self):
        self.maxq = []
    
    def push(self, n):
        # remove all elements less than n
        while self.maxq and self.maxq[-1] < n: 

            self.maxq.pop()
        # then add n to the end
        self.maxq.append(n)
    
    def max(self):
        return self.maxq[0]
    
    def pop(self, n):
        if n == self.maxq[0]:
            self.maxq.pop(0)

class Solution(object):
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        window = MonotonicQueue()
        res = []
        
        for i in range(len(nums)):
            if i < k - 1:
                # first fill the window with the first k - 1 elements
                window.push(nums[i])
            else: 

                # slide the window forward, add new number
                window.push(nums[i])
                # record the maximum value of the current window
                res.append(window.max())
                # remove the old number
                window.pop(nums[i - k + 1])
        return res

import (
	"container/list"
)

type MonotonicQueue struct {
    maxq list.List
}

func (mq *MonotonicQueue) push(n int) {
    // remove all elements smaller than n
    for mq.maxq.Len() > 0 && mq.maxq.Back().Value.(int) < n {

        mq.maxq.Remove(mq.maxq.Back())
    }
    // then add n to the back
    mq.maxq.PushBack(n)
}

func (mq *MonotonicQueue) max() int {
    return mq.maxq.Front().Value.(int)
}

func (mq *MonotonicQueue) pop(n int) {
    if n == mq.maxq.Front().Value.(int) {
        mq.maxq.Remove(mq.maxq.Front())
    }
}

func maxSlidingWindow(nums []int, k int) []int {
    window := MonotonicQueue{maxq: list.List{}}
    res := []int{}

    for i := 0; i < len(nums); i++ {
        if i < k-1 {
            // first fill the window with the first k - 1 elements
            window.push(nums[i])
        } else {
            /* <extend up -100>
            <div class="img-content"><img src="/images/monotonic-queue/1.png" alt class="myimage" loading="lazy" photo-swipe="" /></div>
            */
            // slide the window forward, adding new number
            window.push(nums[i])
            // record the maximum value of the current window
            res = append(res, window.max())
            // remove the old number
            window.pop(nums[i-k+1])
        }
    }
    return res
}

// implementation of monotonic queue
class MonotonicQueue {
    constructor() {
        this.maxq = [];
    }

    push(n) {
        // remove all elements smaller than n
        while (this.maxq.length > 0 && this.maxq[this.maxq.length - 1] < n) {

            this.maxq.pop();
        }
        // then add n to the back
        this.maxq.push(n);
    }

    max() {
        return this.maxq[0];
    }

    pop(n) {
        if (n === this.maxq[0]) {
            this.maxq.shift();
        }
    }
}

function maxSlidingWindow(nums, k) {
    var window = new MonotonicQueue();
    var res = [];
    for (var i = 0; i < nums.length; i++) {
        if (i < k - 1) {
            // first fill the window with the first k - 1 elements
            window.push(nums[i]);
        } else {

            // slide the window forward and add a new number
            window.push(nums[i]);
            // record the maximum value of the current window
            res.push(window.max());
            // remove the old number
            window.pop(nums[i - k + 1]);
        }
    }
    return res;
}

Do not overlook some detailed issues. When implementing MonotonicQueue, we used Java's LinkedList because the linked list structure supports fast insertion and deletion of elements at both the head and tail. Meanwhile, the res in the solution code uses the ArrayList structure, as elements will be accessed by index later, making the array structure more suitable. Pay attention to these details when implementing in other languages.

Regarding the time complexity of the monotonic queue API, readers might be puzzled: the push operation contains a while loop, so the worst-case time complexity should be $O(N)$, and with an additional for loop, the algorithm's time complexity should be $O(N^2)$, right?

Here, we apply amortized analysis as mentioned in the Guide to Algorithm Time and Space Complexity Analysis:

Looking at the push operation alone, the worst-case time complexity is indeed $O(N)$, but the average time complexity is $O(1)$. Typically, we use average complexity rather than the worst-case complexity to measure API interfaces, so the overall time complexity of this algorithm is $O(N)$, not $O(N^2)$.

Alternatively, analyzing from an overall perspective: the algorithm essentially involves adding and removing each element in nums from the window at most once. It is impossible to repeatedly add and remove the same element, so the overall time complexity is $O(N)$.

The space complexity is easy to analyze, which is the size of the window $O(k)$.

Further Exploration

Finally, I pose a few questions for you to consider:

1. The MonotonicQueue class provided in this article only implements the max method. Can you add a min method to return the minimum value of all elements in the queue in $O(1)$ time?

2. The pop method of the MonotonicQueue class provided in this article still requires a parameter, which is not so elegant and goes against the standard queue API. Please fix this defect.

3. Implement the size method of the MonotonicQueue class to return the number of elements in the monotonic queue (note that each push operation might remove elements from the underlying q list, so the number of elements in q is not the number of elements in the monotonic queue).

In other words, can you implement a general-purpose monotonic queue:

// General implementation of a monotonic queue, which
// can efficiently maintain maximum and minimum values
class MonotonicQueue<E extends Comparable<E>> {

    // Standard queue API to add an element to the back of the queue
    public void push(E elem);

    // Standard queue API to pop an element from the front of the queue, following FIFO order
    public E pop();

    // Standard queue API to return the number of elements in the queue
    public int size();

    // Monotonic queue specific API to compute the maximum value in the queue in O(1) time
    public E max();

    // Monotonic queue specific API to compute the minimum value in the queue in O(1) time
    public E min();
}

// General implementation of a monotonic queue, which can
// efficiently maintain the maximum and minimum values
template <typename E>
class MonotonicQueue {
public:
    // Standard queue API, add an element to the end of the queue
    void push(E elem);

    // Standard queue API, remove an element from the
    // front of the queue, following the FIFO order
    E pop();

    // Standard queue API, return the number of elements in the queue
    int size();

    // Monotonic queue specific API, compute the maximum
    // value among the elements in the queue in O(1) time
    E max();

    // Monotonic queue specific API, compute the minimum
    // value among the elements in the queue in O(1) time
    E min();
};

# General implementation of a monotonic queue, can
# efficiently maintain maximum and minimum values
class MonotonicQueue:
    def push(self, elem: 'Comparable') -> None:
        pass
    
    # Standard queue API, pop elements from the front in FIFO order
    def pop(self) -> 'Comparable':
        pass
    
    # Standard queue API, return the number of elements in the queue
    def size(self) -> int:
        pass
    
    # Monotonic queue specific API, calculate the
    # maximum value of elements in the queue in O(1) time
    def max(self) -> 'Comparable':
        pass
    
    # Monotonic queue specific API, calculate the
    # minimum value of elements in the queue in O(1) time
    def min(self) -> 'Comparable':
        pass

// MonotonicQueue is a general implementation of a monotonic
// queue that can efficiently maintain maximum and minimum values
type MonotonicQueue struct{}

type Comparable interface {
    // compare function, the return value -1, 0, 1
    // respectively represents less than, equal to, greater than
    compare(Comparable) int
}

// push adds an element to the end of the queue
func (q *MonotonicQueue) push(elem Comparable) {}

// pop removes an element from the front of the queue, following the first-in-first-out order
func (q *MonotonicQueue) pop() Comparable {}

// size returns the number of elements in the queue
func (q *MonotonicQueue) size() int {}

// max is a specific API of the monotonic queue that
// calculates the maximum value of elements in O(1) time
func (q *MonotonicQueue) max() Comparable {}

// min is a specific API of the monotonic queue that
// calculates the minimum value of elements in O(1) time
func (q *MonotonicQueue) min() Comparable {}

// General implementation of a monotonic queue, can
// efficiently maintain the maximum and minimum values
class MonotonicQueue {
    // Standard queue API, add elements to the end of the queue
    push(elem) {}

    // Standard queue API, remove elements from the front of the queue, following the FIFO order
    pop() {}

    // Standard queue API, return the number of elements in the queue
    size() {}

    // Monotonic queue specific API, calculate the
    // maximum value of elements in the queue in O(1) time
    max() {}

    // Monotonic queue specific API, calculate the
    // minimum value of elements in the queue in O(1) time
    min() {}
}

I will provide a general implementation of the monotonic queue and classic exercises in General Implementation and Applications of Monotonic Queue. For more data structure design problems, see Classic Exercises on Data Structure Design.