Implementing LRU Cache like Building a Lego

labuladongOriginalAbout 7716 words

This article will resolve

LeetCode	Difficulty
146. LRU Cache	🟠

Prerequisites

Before reading this article, you should first learn:

The LRU algorithm is a cache eviction strategy. Its principle is not difficult, but writing a bug-free algorithm in an interview requires skill, involving multiple layers of abstraction and breakdown of data structures. This article will guide you to write elegant code.

The key data structure used in the LRU algorithm is the hash-linked list, LinkedHashMap. The Hands-on Guide to Implementing Hash Linked List in the data structure basics section explains the principles and code implementation of hash-linked lists. If you haven't read it, it's okay; this article will explain the core principles of hash-linked lists again to facilitate the implementation of the LRU algorithm.

Computer cache capacity is limited. If the cache is full, some content needs to be deleted to make space for new content. But the question is, what content should be deleted? We want to remove the cache that is not useful and keep the useful data in the cache for future use. So, what kind of data do we consider "useful"?

The LRU cache eviction algorithm is a common strategy. LRU stands for Least Recently Used, meaning that we consider recently used data to be "useful" and data that hasn't been used for a long time to be useless. When the memory is full, we delete the data that hasn't been used for the longest time.

For example, Android phones allow apps to run in the background. If I open "Settings," "Phone Manager," and "Calendar" one after another, the order in the background is like this:

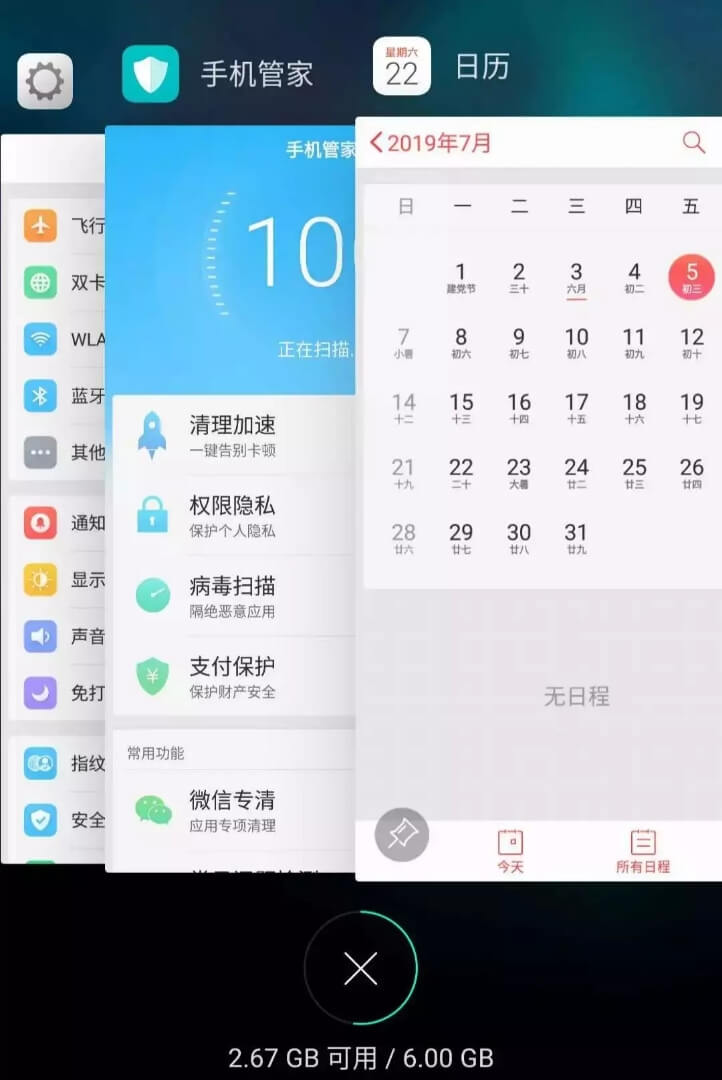
But if I then access the "Settings" interface, "Settings" will be moved to the front, like this:

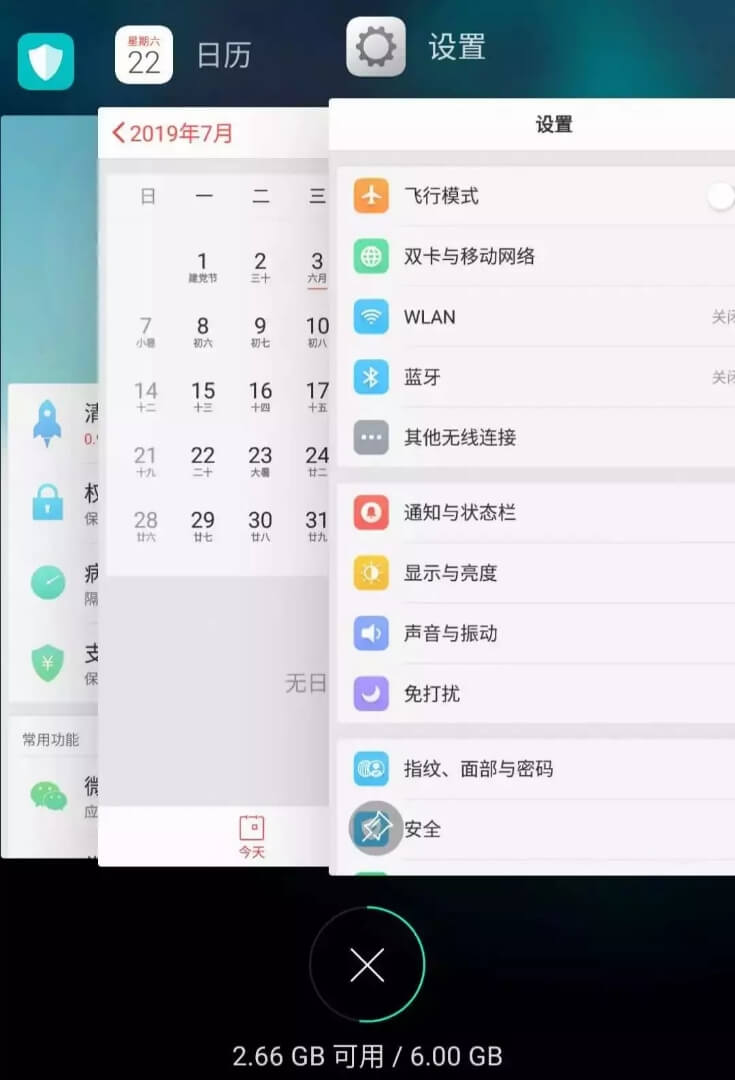
Assume my phone only allows three apps to run simultaneously, and it's already full. If I open a new app "Clock," I must close one app to free up space for "Clock." Which one should be closed?

According to the LRU strategy, the bottom "Phone Manager" is closed because it is the least recently used, and the new app is placed at the top:

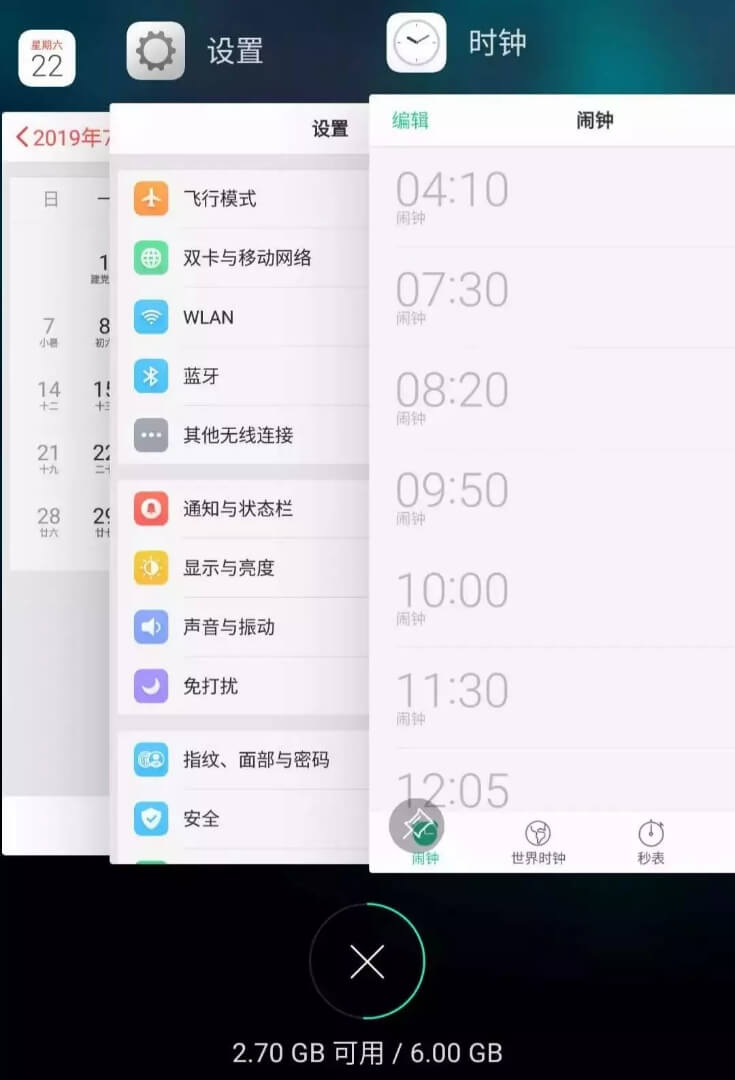
Now you should understand the LRU (Least Recently Used) strategy. Of course, there are other cache eviction strategies, such as evicting based on access frequency (LFU strategy) rather than access order. Each has its application scenarios. This article explains the LRU algorithm strategy, and I will explain the LFU algorithm in LFU Algorithm Details.

1. LRU Algorithm Description

LeetCode Problem 146 "LRU Cache" requires you to design a data structure:

First, it should accept a capacity parameter as the maximum cache capacity, then implement two APIs: a put(key, val) method to store key-value pairs and a get(key) method to retrieve the val corresponding to key. If key does not exist, it returns -1.

Note that the get and put methods must have a time complexity of $O(1)$ . Let's look at a specific example to see how the LRU algorithm works:

java

// the cache capacity is 2
LRUCache cache = new LRUCache(2);
// you can understand the cache as a queue
// assume the left side is the head of the queue and the right side is the tail
// the most recently used is at the head of the
// queue, and the least recently used is at the tail
// parentheses represent the key-value pair (key, val)

cache.put(1, 1);
// cache = [(1, 1)]

cache.put(2, 2);
// cache = [(2, 2), (1, 1)]

// return 1
cache.get(1);
// cache = [(1, 1), (2, 2)]
// explanation: because key 1 was recently accessed, it is moved to the head of the queue
// return the value corresponding to key 1, which is 1

cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// explanation: the cache is full, need to delete content to make space
// prefer to delete the least recently used data, which is the data at the tail
// then insert the new data at the head of the queue

// return -1 (not found)
cache.get(2);
// cache = [(3, 3), (1, 1)]
// explanation: there is no data with key 2 in the cache

cache.put(1, 4);    
// cache = [(1, 4), (3, 3)]
// explanation: key 1 already exists, overwrite the original value 1 with 4
// don't forget to also move the key-value pair to the head of the queue

cpp

// the cache capacity is 2
LRUCache* cache = new LRUCache(2);
// you can understand cache as a queue
// assume the left is the head of the queue and the right is the tail
// the most recently used is at the head, and the least recently used is at the tail
// parentheses represent the key-value pair (key, val)

cache->put(1, 1);
// cache = [(1, 1)]

cache->put(2, 2);
// cache = [(2, 2), (1, 1)]

// return 1
cache->get(1);
// cache = [(1, 1), (2, 2)]
// explanation: because key 1 was recently accessed, it is moved to the head
// return the value corresponding to key 1

cache->put(3, 3);    
// cache = [(3, 3), (1, 1)]
// explanation: the cache is full, need to delete content to make space
// preferentially delete the least recently used data, which is the data at the tail
// then insert the new data at the head

// return -1 (not found)
cache->get(2);
// cache = [(3, 3), (1, 1)]
// explanation: there is no data with key 2 in the cache

cache->put(1, 4);    
// cache = [(1, 4), (3, 3)]
// explanation: key 1 already exists, overwrite the original value 1 with 4
// don't forget to also move the key-value pair to the head

python

# the cache capacity is 2
cache = LRUCache(2)

# you can understand cache as a queue
# assume the left is the head of the queue and the right is the tail
# the most recently used is at the head of the queue, and the least recently used is at the tail
# parentheses represent key-value pairs (key, val)

cache.put(1, 1)
# cache = [(1, 1)]

cache.put(2, 2)
# cache = [(2, 2), (1, 1)]

# return 1
cache.get(1)
# explanation: because key 1 was recently accessed, it is moved to the head of the queue
# return the value corresponding to key 1
# cache = [(1, 1), (2, 2)]

cache.put(3, 3)
# cache = [(3, 3), (1, 1)]
# explanation: the cache is full, need to delete content to make space
# priority is given to deleting the least recently
# used data, which is the data at the tail of the queue
# then insert the new data at the head of the queue

# return -1 (not found)
cache.get(2)
# explanation: there is no data with key 2 in the cache
# cache = [(3, 3), (1, 1)]

cache.put(1, 4)
# cache = [(1, 4), (3, 3)]
# explanation: key 1 already exists, overwrite the original value 1 with 4
# don't forget to also move the key-value pair to the head of the queue

// Create an LRU Cache with a capacity of 2
cache := Constructor(2)

// You can think of the cache as a queue
// Assuming the left is the head of the queue and the right is the tail
// The most recently used is at the head of the
// queue, and the least recently used is at the tail
// Parentheses represent key-value pairs (key, val)

cache.Put(1, 1)
// cache = [(1, 1)]

cache.Put(2, 2)
// cache = [(2, 2), (1, 1)]

// Return 1
cache.Get(1)
// cache = [(1, 1), (2, 2)]
// Explanation: Because key 1 was recently accessed, it is moved to the head of the queue
// Return the value corresponding to key 1

cache.Put(3, 3)
// cache = [(3, 3), (1, 1)]
// Explanation: The cache capacity is full, need to
// remove the least recently used element to make room
// Prioritize deleting the least recently used data, which is the data at the tail of the queue
// Then insert the new data at the head of the queue

// Return -1 (not found)
cache.Get(2)
// cache = [(3, 3), (1, 1)]
// Explanation: The cache does not contain the data with key 2

cache.Put(1, 4)
// cache = [(1, 4), (3, 3)]
// Explanation: Key 1 already exists, overwrite the original value 1 with 4
// Don't forget to also move the key-value pair to the head of the queue

javascript

// the cache capacity is 2
var cache = new LRUCache(2);
// you can understand the cache as a queue
// assuming the left is the head of the queue and the right is the tail
// the most recently used is at the head of the
// queue, and the least recently used is at the tail
// parentheses represent key-value pairs (key, val)

cache.put(1, 1);
// cache = [(1, 1)]

cache.put(2, 2);
// cache = [(2, 2), (1, 1)]

// return 1
console.log(cache.get(1));
// cache = [(1, 1), (2, 2)]
// explanation: because key 1 was recently accessed, it is moved to the head of the queue
// return the value corresponding to key 1

cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// explanation: the cache is full, need to remove content to make space
// prioritize removing the least recently used data, which is the data at the tail of the queue
// then insert the new data at the head of the queue

// return -1 (not found)
console.log(cache.get(2));
// cache = [(3, 3), (1, 1)]
// explanation: there is no data with key 2 in the cache

cache.put(1, 4);    
// cache = [(1, 4), (3, 3)]
// explanation: key 1 already exists, overwrite the original value 1 with 4
// also, don't forget to move the key-value pair to the head of the queue

II. LRU Algorithm Design

Analyzing the above operations, to ensure that the time complexity of the put and get methods is O(1), we can summarize the necessary conditions for the cache data structure:

Clearly, the elements in the cache must have a sequence to distinguish between recently used and long-unused data. When the capacity is full, the least recently used element should be removed to make space.
We need to quickly find whether a certain key exists in the cache and obtain the corresponding val.
Each time a key in the cache is accessed, this element needs to be made the most recently used, which means the cache must support quick insertion and deletion of elements at any position.

So, what data structure meets these conditions? A hash table allows fast lookup, but the data is unordered. A linked list is ordered and allows fast insertion and deletion, but lookup is slow. Therefore, combining them forms a new data structure: a hash-linked list, LinkedHashMap.

The core data structure of the LRU cache algorithm is this hash-linked list, a combination of a doubly linked list and a hash table. It looks like this:

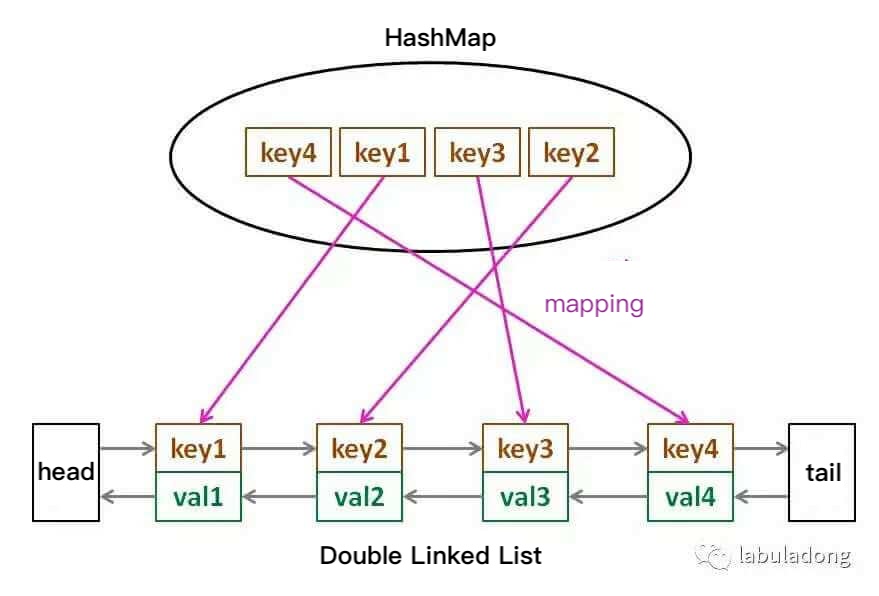
Using this structure, let's analyze the three conditions one by one:

If we always add elements to the end of the list, then obviously, the closer to the end an element is, the more recently it's been used. The closer to the head an element is, the less recently it's been used.
For a specific key, we can quickly locate the node in the linked list via the hash table and obtain the corresponding val.
A linked list naturally supports quick insertion and deletion at any position by adjusting pointers. However, a traditional linked list cannot quickly access an element at a specific index. Here, with the help of a hash table, we can quickly map a key to any linked list node for insertion and deletion.

Readers might ask why a doubly linked list is needed instead of a singly linked list? Also, since the key is already stored in the hash table, why does the linked list need to store both key and val? Wouldn't storing just val suffice?

These questions can only be answered through implementation. The rationale behind this design will become clear once we personally implement the LRU algorithm, so let's start coding!

3. Code Implementation

Many programming languages have built-in libraries for hash-linked lists or functions similar to LRU. However, to help understand the algorithm's details, we will first implement the LRU algorithm from scratch and then use Java's built-in LinkedHashMap to implement it again.

First, let's write out the node class of a doubly linked list. To simplify, assume both key and val are of type int:

java

class Node {
    public int key, val;
    public Node next, prev;
    public Node(int k, int v) {
        this.key = k;
        this.val = v;
    }
}

cpp

class Node {
    public:
        int key, val;
        Node* next;
        Node* prev;
        Node(int k, int v){
            this->key = k;
            this->val = v;
        }
};

python

class Node:
    def __init__(self, k: int, v: int):
        self.key = k
        self.val = v
        self.next = None
        self.prev = None

type Node struct {
    key, val int
    next, prev *Node
}

func NewNode(k, v int) *Node {
    return &Node{key: k, val: v}
}

javascript

var Node = function(k, v) {
  this.key = k;
  this.val = v;
  this.next = null;
  this.prev = null;
};

Then, using our Node type, we build a doubly linked list and implement several necessary APIs for the LRU algorithm:

java

class DoubleList {  
    // virtual head and tail nodes
    private Node head, tail;  
    // number of elements in the linked list
    private int size;
    
    public DoubleList() {
        // initialize the data of the doubly linked list
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head.next = tail;
        tail.prev = head;
        size = 0;
    }

    // add node x to the end of the list, time O(1)
    public void addLast(Node x) {
        x.prev = tail.prev;
        x.next = tail;
        tail.prev.next = x;
        tail.prev = x;
        size++;
    }

    // remove node x from the list (x is guaranteed to exist)
    // since it's a doubly linked list and the target Node is given, time O(1)
    public void remove(Node x) {
        x.prev.next = x.next;
        x.next.prev = x.prev;
        size--;
    }
    
    // remove the first node from the list and return it, time O(1)
    public Node removeFirst() {
        if (head.next == tail)
            return null;
        Node first = head.next;
        remove(first);
        return first;
    }

    // return the length of the list, time O(1)
    public int size() { return size; }

}

cpp

class DoubleList {
private:
    // virtual head and tail nodes
    Node* head;
    Node* tail;
    // number of elements in the list
    int size;

public:
    DoubleList() {
        // initialize the data of the doubly linked list
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head->next = tail;
        tail->prev = head;
        size = 0;
    }

    // add node x to the end of the list, time complexity O(1)
    void addLast(Node* x) {
        x->prev = tail->prev;
        x->next = tail;
        tail->prev->next = x;
        tail->prev = x;
        size++;
    }

    // remove node x from the list (x is guaranteed to exist)
    // since it is a doubly linked list and the target Node is given, time complexity O(1)
    void remove(Node* x) {
        x->prev->next = x->next;
        x->next->prev = x->prev;
        size--;
    }

    // remove the first node of the list and return it, time complexity O(1)
    Node* removeFirst() {
        if (head->next == tail)
            return nullptr;
        Node* first = head->next;
        remove(first);
        return first;
    }

    // return the length of the list, time complexity O(1)
    int getSize() { return size; }
};

python

class DoubleList:
    # virtual head and tail nodes
    def __init__(self):
        self.head = Node(0, 0)
        self.tail = Node(0, 0)
        self.head.next = self.tail
        self.tail.prev = self.head
        self.size = 0
    
    # add node x to the end of the list, time complexity O(1)
    def addLast(self, x: Node):
        x.prev = self.tail.prev
        x.next = self.tail
        self.tail.prev.next = x
        self.tail.prev = x
        self.size += 1
    
    # remove node x from the list (x is guaranteed to exist)
    # since it's a doubly linked list and the target Node is given, time complexity O(1)
    def remove(self, x: Node):
        x.prev.next = x.next
        x.next.prev = x.prev
        self.size -= 1
    
    # remove the first node of the list and return it, time complexity O(1)
    def removeFirst(self) -> Node:
        if self.head.next == self.tail:
            return None
        first = self.head.next
        self.remove(first)
        return first
    
    # return the size of the list, time complexity O(1)
    def size(self) -> int:
        return self.size

type DoubleList struct {
    head, tail *Node
    size       int
}

func NewDoubleList() *DoubleList {
    // initialize the data of the doubly linked list
    head := &Node{key: 0, val: 0}
    tail := &Node{key: 0, val: 0}
    head.next, tail.prev = tail, head
    return &DoubleList{head: head, tail: tail, size: 0}
}

// add node x to the end of the list, time O(1)
func (this *DoubleList) AddLast(x *Node) {
    x.prev = this.tail.prev
    x.next = this.tail
    this.tail.prev.next = x
    this.tail.prev = x
    this.size++
}

// remove node x from the list (x is guaranteed to exist)
// since it is a doubly linked list and the target Node is given, time O(1)
func (this *DoubleList) Remove(x *Node) {
    x.prev.next = x.next
    x.next.prev = x.prev
    this.size--
}

// remove the first node of the list and return it, time O(1)
func (this *DoubleList) RemoveFirst() *Node {
    if this.head.next == this.tail {
        return nil
    }
    first := this.head.next
    this.Remove(first)
    return first
}

// return the length of the list, time O(1)
func (this *DoubleList) Size() int {
    return this.size
}

javascript

var DoubleList = function() {
    // virtual head and tail nodes
    this.head = new Node(0, 0);
    this.tail = new Node(0, 0);
    
    // number of elements in the list
    this.size = 0;

    // initialize the data of the doubly linked list
    this.head.next = this.tail;
    this.tail.prev = this.head;
};

// add node x to the end of the list, time complexity O(1)
DoubleList.prototype.addLast = function(x) {
    x.prev = this.tail.prev;
    x.next = this.tail;
    this.tail.prev.next = x;
    this.tail.prev = x;
    this.size++;
};

// remove node x from the list (x is guaranteed to exist)
// since it's a doubly linked list and the target Node is given, time complexity O(1)
DoubleList.prototype.remove = function(x) {
    x.prev.next = x.next;
    x.next.prev = x.prev;
    this.size--;
};

// remove the first node of the list and return it, time complexity O(1)
DoubleList.prototype.removeFirst = function() {
    if (this.head.next == this.tail)
        return null;
    var first = this.head.next;
    this.remove(first);
    return first;
};

// return the length of the list, time complexity O(1)
DoubleList.prototype.size = function() {
    return this.size;
};

If you are not familiar with linked list operations, refer to the article Hands-on Implementation of Doubly Linked List.

At this point, we can answer the question, "Why must we use a doubly linked list?" It's because we need a delete operation. Deleting a node requires not only obtaining the pointer to the node itself but also manipulating the pointer of its predecessor, which a doubly linked list supports to ensure the operation's time complexity is O(1).

Important

Note that the API of our implemented doubly linked list can only insert from the tail, meaning that the data near the tail is the most recently used, while the data near the head is the least recently used.

With the implementation of the doubly linked list, we only need to combine it with a hash table in the LRU algorithm. Let's first set up the code framework:

java

class LRUCache {
    // key -> Node(key, val)
    private HashMap<Integer, Node> map;
    // Node(k1, v1) <-> Node(k2, v2)...
    private DoubleList cache;
    // maximum capacity
    private int cap;
    
    public LRUCache(int capacity) {
        this.cap = capacity;
        map = new HashMap<>();
        cache = new DoubleList();
    }
}

cpp

class LRUCache {
private:
    // key -> Node(key, val)
    unordered_map<int, Node*> map;
    // Node(k1, v1) <-> Node(k2, v2)...
    DoubleList cache;
    // maximum capacity
    int cap;

public:
    LRUCache(int capacity) {
        this->cap = capacity;
    }
};

python

class LRUCache:
    def __init__(self, capacity: int):
        # key -> Node(key, val)
        self.map = {}
        # Node(k1, v1) <-> Node(k2, v2)...
        self.cache = DoubleList()
        # maximum capacity
        self.cap = capacity

type LRUCache struct {
    // key -> Node(key, val)
    _map map[int]*Node
    // Node(k1, v1) <-> Node(k2, v2)...
    cache *DoubleList
    // maximum capacity
    cap int
}

func Constructor(capacity int) LRUCache {
    return LRUCache{
        map_:  make(map[int]*Node),
        cache: NewDoubleList(),
        cap:   capacity,
    }
}

javascript

var LRUCache = function(capacity) {
    // key -> Node(key, val)
    this.map = new Map();
    // Node(k1, v1) <-> Node(k2, v2)...
    this.cache = new DoubleList();
    // maximum capacity
    this.cap = capacity;
};

Do not rush to implement the get and put methods of the LRU algorithm. Since we need to maintain both a doubly linked list cache and a hash table map, it's easy to miss some operations, such as deleting a key in cache but forgetting to delete it in map.

An effective way to solve this problem is to provide an abstract API layer over these two data structures.

This means letting the main methods get and put of LRU avoid directly manipulating the details of map and cache. We can first implement the following functions:

java

class LRUCache {
    // To save space, the previous code part is omitted...

    // promote a key to the most recently used
    private void makeRecently(int key) {
        Node x = map.get(key);
        // first remove this node from the linked list
        cache.remove(x);
        // reinsert it at the end of the queue
        cache.addLast(x);
    }

    // add the most recently used element
    private void addRecently(int key, int val) {
        Node x = new Node(key, val);
        // the tail of the linked list is the most recently used element
        cache.addLast(x);
        // don't forget to add the key mapping in the map
        map.put(key, x);
    }

    // delete a certain key
    private void deleteKey(int key) {
        Node x = map.get(key);
        // remove from the linked list
        cache.remove(x);
        // delete from the map
        map.remove(key);
    }

    // remove the least recently used element
    private void removeLeastRecently() {
        // the first element in the linked list is the least recently used
        Node deletedNode = cache.removeFirst();
        // also, don't forget to remove its key from the map
        int deletedKey = deletedNode.key;
        map.remove(deletedKey);
    }
}

cpp

class LRUCache {
private:
    // For the sake of brevity, the previous given code part is omitted...

    // promote a certain key to be recently used
    void makeRecently(int key) {
        Node* x = map[key];
        // first remove this node from the list
        cache.remove(x);
        // reinsert it at the end of the queue
        cache.addLast(x);
    }

    // add the recently used element
    void addRecently(int key, int val) {
        Node* x = new Node(key, val);
        // the tail of the list is the most recently used element
        cache.addLast(x);
        // don't forget to add the mapping of the key in the map
        map[key] = x;
    }

    // delete a certain key
    void deleteKey(int key) {
        Node* x = map[key];
        // remove it from the list
        cache.remove(x);
        // delete from the map
        map.erase(key);
    }

    // remove the least recently used element
    void removeLeastRecently() {
        // the first element at the head of the list is the least recently used
        Node* deletedNode = cache.removeFirst();
        // also, don't forget to delete its key from the map
        int deletedKey = deletedNode->key;
        map.erase(deletedKey);
    }
};

python

class LRUCache:
    # For the sake of brevity, the previous part of the code is omitted...

    # Promote a certain key to recently used
    def makeRecently(self, key: int):
        x = self.map[key]
        # First, remove this node from the linked list
        self.cache.remove(x)
        # Reinsert it at the end of the queue
        self.cache.addLast(x)

    # Add the most recently used element
    def addRecently(self, key: int, val: int):
        x = Node(key, val)
        # The tail of the linked list is the most recently used element
        self.cache.addLast(x)
        # Don't forget to add the key mapping in the map
        self.map[key] = x

    # Delete a certain key
    def deleteKey(self, key: int):
        x = self.map[key]
        # Remove it from the linked list
        self.cache.remove(x)
        # Delete it from the map
        self.map.pop(key)

    # Remove the least recently used element
    def removeLeastRecently(self):
        # The first element at the head of the linked list is the least recently used
        deletedNode = self.cache.removeFirst()
        # Also, don't forget to delete its key from the map
        deletedKey = deletedNode.key
        self.map.pop(deletedKey)

// For the sake of brevity, the previous code is omitted...

// Promote a certain key to the most recently used
func (this *LRUCache) makeRecently(key int) {
    x := this._map[key]
    // First, remove this node from the list
    this.cache.Remove(x)
    // Re-insert it at the end of the queue
    this.cache.AddLast(x)
}

// Add the most recently used element
func (this *LRUCache) addRecently(key, val int) {
    x := NewNode(key, val)
    // The tail of the list is the most recently used element
    this.cache.AddLast(x)
    // Don't forget to add the mapping of the key in the map
    this._map[key] = x
}

// Delete a certain key
func (this *LRUCache) deleteKey(key int) {
    x := this._map[key]
    // Remove it from the list
    this.cache.Remove(x)
    // Delete from the map
    delete(this._map, key)
}

// Remove the least recently used element
func (this *LRUCache) removeLeastRecently() {
    // The first element in the list is the least recently used
    deletedNode := this.cache.RemoveFirst()
    // Also, don't forget to delete its key from the map
    deletedKey := deletedNode.key
    delete(this._map, deletedKey)
}

javascript

// For the sake of brevity, the previous code section is omitted...

// Promote a certain key to the most recently used
LRUCache.prototype.makeRecently = function(key) {
    var x = this.map.get(key);
    // First, remove this node from the linked list
    this.cache.remove(x);
    // Re-insert it at the end of the queue
    this.cache.addLast(x);
};

// Add the most recently used element
LRUCache.prototype.addRecently = function(key, val) {
    var x = new Node(key, val);
    // The tail of the linked list is the most recently used element
    this.cache.addLast(x);
    // Don't forget to add the key mapping in the map
    this.map.set(key, x);
};

// Delete a certain key
LRUCache.prototype.deleteKey = function(key) {
    var x = this.map.get(key);
    // Remove from the linked list
    this.cache.remove(x);
    // Delete from the map
    this.map.delete(key);
};

// Remove the least recently used element
LRUCache.prototype.removeLeastRecently = function() {
    // The first element of the linked list is the least recently used
    var deletedNode = this.cache.removeFirst();
    // Also, don't forget to delete its key from the map
    var deletedKey = deletedNode.key;
    this.map.delete(deletedKey);
};

Here, we can answer the previous question, "Why store both key and val in the linked list instead of just val?" In the removeLeastRecently function, we need to use deletedNode to get deletedKey.

That is, when the cache is full, we need to delete not only the last Node but also the key mapped to that node in map, which can only be obtained from Node. If Node only stored val, we would not know what the key is, and thus could not delete the key in map, leading to errors.

The above methods are simple operation encapsulations. Using these functions can avoid directly manipulating the cache linked list and the map hash table. Next, let's implement the get method of the LRU algorithm:

java

class LRUCache {
    // To save space, the previous code is omitted...

    public int get(int key) {
        if (!map.containsKey(key)) {
            return -1;
        }
        // promote the data to the most recently used
        makeRecently(key);
        return map.get(key).val;
    }
}

cpp

class LRUCache {
private:
    // For brevity, the previous given code is omitted...

public:
    int get(int key) {
        if (!map.count(key)) {
            return -1;
        }
        // promote the data to the most recently used
        makeRecently(key);
        return map[key]->val;
    }
};

python

class LRUCache:
    # To save space, the previous code part is omitted...

    def get(self, key: int) -> int:
        if key not in self.map:
            return -1
        
        # promote this data to most recently used
        self.makeRecently(key)
        return self.map[key].val

// For the sake of brevity, the previous code is omitted...

func (this *LRUCache) Get(key int) int {
    if _, ok := this._map[key]; !ok {
        return -1
    }
    // Promote the data to most recently used
    this.makeRecently(key)
    return this._map[key].val
}

javascript

// To save space, the previous code is omitted...

LRUCache.prototype.get = function(key) {
    if (!this.map.has(key)) {
        return -1;
    }
    // promote the data to most recently used
    this.makeRecently(key);
    return this.map.get(key).val;
};

The put method is slightly more complex. Let's draw a diagram to clarify its logic:

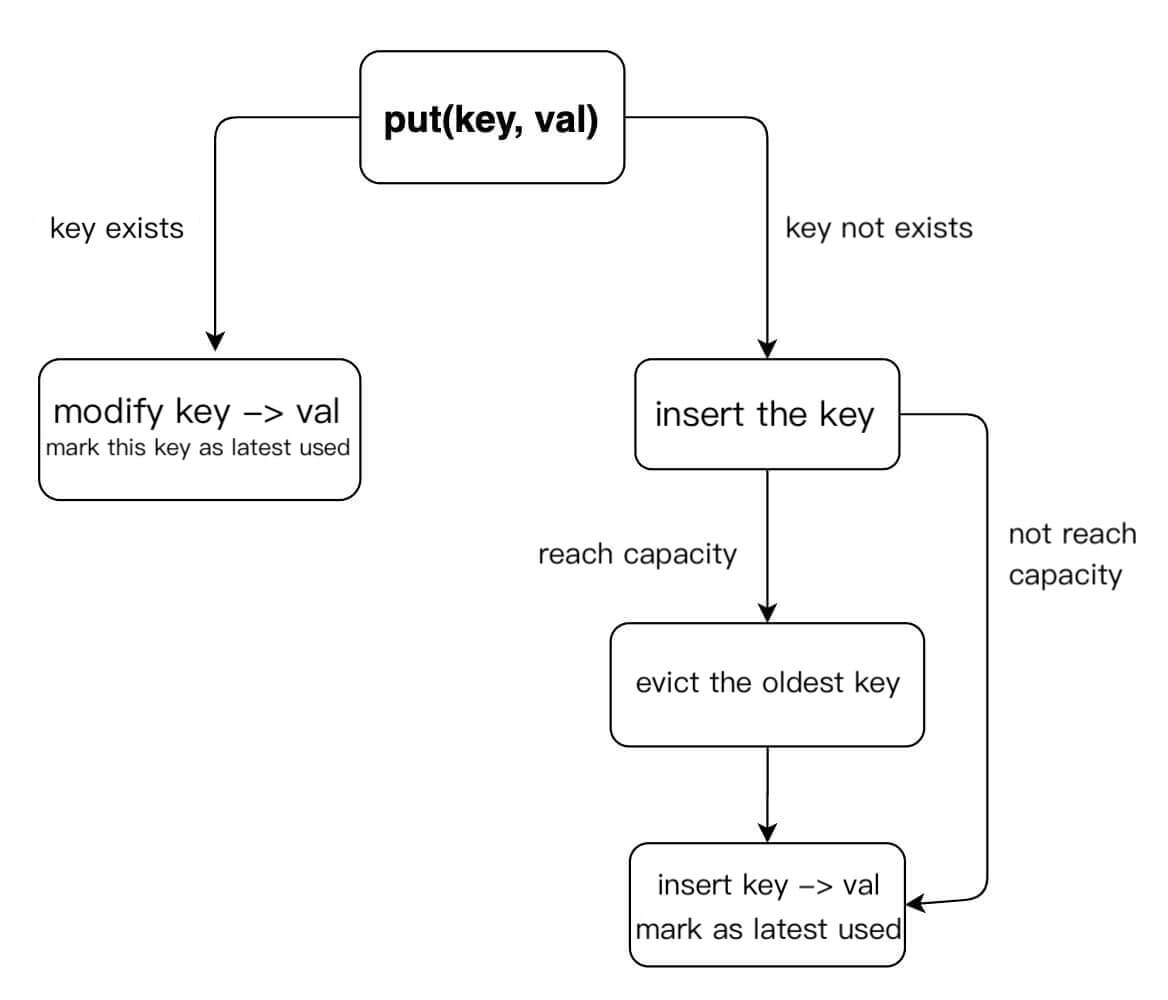
With this, we can easily write the code for the put method:

java

class LRUCache {
    // To save space, the previous given code part is omitted...
    
    public void put(int key, int val) {
        if (map.containsKey(key)) {
            // delete the old data
            deleteKey(key);
            // the newly inserted data is the most recently used data
            addRecently(key, val);
            return;
        }
        
        if (cap == cache.size()) {
            // remove the least recently used element
            removeLeastRecently();
        }
        // add as the most recently used element
        addRecently(key, val);
    }
}

cpp

class LRUCache {
private:
    // To save space, the previous code is omitted...

public:
    void put(int key, int val) {
        if (map.count(key)) {
            // delete the old data
            deleteKey(key);
            // the newly inserted data is the most recently used data
            addRecently(key, val);
            return;
        }

        if (cap == cache.getSize()) {
            // delete the least recently used element
            removeLeastRecently();
        }
        // add as the most recently used element
        addRecently(key, val);
    }
};

python

class LRUCache:
    # To save space, the previous code part is omitted...

    def put(self, key: int, val: int) -> None:
        if key in self.map:
            # delete the old data
            self.deleteKey(key)
            # the newly inserted data is the most recently used data
            self.addRecently(key, val)
            return
        
        if self.cap == self.cache.size():
            # delete the least recently used element
            self.removeLeastRecently()
        # add as the most recently used element
        self.addRecently(key, val)

// To save space, the previous code part is omitted...

func (this *LRUCache) Put(key, val int) {
    if _, ok := this._map[key]; ok {
        // delete the old data
        this.deleteKey(key)
        // the newly inserted data is the most recently used data
        this.addRecently(key, val)
        return
    }

    if this.cap == this.cache.Size() {
        // delete the least recently used element
        this.removeLeastRecently()
    }
    // add as the most recently used element
    this.addRecently(key, val)
}

javascript

// To save space, the previous code part is omitted...

LRUCache.prototype.put = function(key, val) {
    if (this.map.has(key)) {
        // delete the old data
        this.deleteKey(key);
        // the newly inserted data is the most recently used data
        this.addRecently(key, val);
        return;
    }

    if (this.cap === this.cache.size()) {
        // delete the least recently used element
        this.removeLeastRecently();
    }
    // add as the most recently used element
    this.addRecently(key, val);
};

At this point, you should have a full understanding of the LRU algorithm's principles and implementation. Here's the complete implementation:

java

// doubly linked list node
class Node {
    public int key, val;
    public Node next, prev;
    public Node(int k, int v) {
        this.key = k;
        this.val = v;
    }
}

// doubly linked list
class DoubleList {  
    // virtual head and tail nodes
    private Node head, tail;  
    // number of elements in the linked list
    private int size;
    
    public DoubleList() {
        // initialize the data of the doubly linked list
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head.next = tail;
        tail.prev = head;
        size = 0;
    }

    // add node x to the end of the list, time O(1)
    public void addLast(Node x) {
        x.prev = tail.prev;
        x.next = tail;
        tail.prev.next = x;
        tail.prev = x;
        size++;
    }

    // remove node x from the list (x is guaranteed to exist)
    // since it's a doubly linked list and the target Node is given, time O(1)
    public void remove(Node x) {
        x.prev.next = x.next;
        x.next.prev = x.prev;
        size--;
    }
    
    // remove the first node from the list and return it, time O(1)
    public Node removeFirst() {
        if (head.next == tail)
            return null;
        Node first = head.next;
        remove(first);
        return first;
    }

    // return the length of the list, time O(1)
    public int size() { return size; }

}


class LRUCache {
    // key -> Node(key, val)
    private HashMap<Integer, Node> map;
    // Node(k1, v1) <-> Node(k2, v2)...
    private DoubleList cache;
    // maximum capacity
    private int cap;
    
    public LRUCache(int capacity) {
        this.cap = capacity;
        map = new HashMap<>();
        cache = new DoubleList();
    }
    
    public int get(int key) {
        if (!map.containsKey(key)) {
            return -1;
        }
        // promote this data to the most recently used
        makeRecently(key);
        return map.get(key).val;
    }
    
    public void put(int key, int val) {
        if (map.containsKey(key)) {
            // remove the old data
            deleteKey(key);
            // the newly inserted data is the most recently used
            addRecently(key, val);
            return;
        }
        
        if (cap == cache.size()) {
            // remove the least recently used element
            removeLeastRecently();
        }
        // add as the most recently used element
        addRecently(key, val);
    }
    
    private void makeRecently(int key) {
        Node x = map.get(key);
        // first remove this node from the list
        cache.remove(x);
        // reinsert it at the end of the list
        cache.addLast(x);
    }

    private void addRecently(int key, int val) {
        Node x = new Node(key, val);
        // the end of the list is the most recently used element
        cache.addLast(x);
        // don't forget to add the key mapping in the map
        map.put(key, x);
    }

    private void deleteKey(int key) {
        Node x = map.get(key);
        // remove from the list
        cache.remove(x);
        // remove from the map
        map.remove(key);
    }

    private void removeLeastRecently() {
        // the first element at the head of the list is the least recently used
        Node deletedNode = cache.removeFirst();
        // also don't forget to remove its key from the map
        int deletedKey = deletedNode.key;
        map.remove(deletedKey);
    }
}

cpp

// doubly linked list node
class Node {
public:
    int key, val;
    Node* next, *prev;
    Node(int k, int v) : key(k), val(v), next(nullptr), prev(nullptr) {}
};

// doubly linked list
class DoubleList {
private:
    // virtual head and tail nodes
    Node* head;
    Node* tail;
    // number of elements in the list
    int size;

public:
    DoubleList() {
        // initialize the data of the doubly linked list
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head->next = tail;
        tail->prev = head;
        size = 0;
    }

    // add node x to the end of the list, time complexity O(1)
    void addLast(Node* x) {
        x->prev = tail->prev;
        x->next = tail;
        tail->prev->next = x;
        tail->prev = x;
        size++;
    }

    // remove node x from the list (x is guaranteed to exist)
    // since it is a doubly linked list and the target Node is given, time complexity O(1)
    void remove(Node* x) {
        x->prev->next = x->next;
        x->next->prev = x->prev;
        size--;
    }

    // remove the first node of the list and return it, time complexity O(1)
    Node* removeFirst() {
        if (head->next == tail)
            return nullptr;
        Node* first = head->next;
        remove(first);
        return first;
    }

    // return the length of the list, time complexity O(1)
    int getSize() { return size; }
};

class LRUCache {
private:
    // key -> Node(key, val)
    unordered_map<int, Node*> map;
    // Node(k1, v1) <-> Node(k2, v2)...
    DoubleList cache;
    // maximum capacity
    int cap;

public:
    LRUCache(int capacity) {
        this->cap = capacity;
    }

    int get(int key) {
        if (!map.count(key)) {
            return -1;
        }
        // promote this data as the most recently used
        makeRecently(key);
        return map[key]->val;
    }

    void put(int key, int val) {
        if (map.count(key)) {
            // delete the old data
            deleteKey(key);
            // the newly inserted data is the most recently used data
            addRecently(key, val);
            return;
        }

        if (cap == cache.getSize()) {
            // remove the least recently used element
            removeLeastRecently();
        }
        // add as the most recently used element
        addRecently(key, val);
    }

    void makeRecently(int key) {
        Node* x = map[key];
        // first remove this node from the list
        cache.remove(x);
        // reinsert it at the end of the list
        cache.addLast(x);
    }

    void addRecently(int key, int val) {
        Node* x = new Node(key, val);
        // the end of the list is the most recently used element
        cache.addLast(x);
        // don't forget to add the key mapping in the map
        map[key] = x;
    }

    void deleteKey(int key) {
        Node* x = map[key];
        // remove from the list
        cache.remove(x);
        // remove from the map
        map.erase(key);
    }

    void removeLeastRecently() {
        // the first element at the head of the list is the least recently used
        Node* deletedNode = cache.removeFirst();
        // also don't forget to remove its key from the map
        int deletedKey = deletedNode->key;
        map.erase(deletedKey);
    }
};

python

class Node:
    def __init__(self, k, v):
        self.key = k
        self.val = v
        self.next = None
        self.prev = None

class DoubleList:
    def __init__(self):
        # head and tail dummy nodes
        self.head = Node(0, 0)
        self.tail = Node(0, 0)
        # number of elements in the list
        self._size = 0

        # initialize the doubly linked list
        self.head.next = self.tail
        self.tail.prev = self.head

    # add node x to the end of the list, time complexity O(1)
    def addLast(self, x):
        x.prev = self.tail.prev
        x.next = self.tail
        self.tail.prev.next = x
        self.tail.prev = x
        self._size += 1

    # remove node x from the list (x must exist)
    # since it's a doubly linked list and x is the target node, time complexity O(1)
    def remove(self, x):
        x.prev.next = x.next
        x.next.prev = x.prev
        self._size -= 1

    # remove the first node in the list and return it, time complexity O(1)
    def removeFirst(self):
        if self.head.next == self.tail:
            return None
        first = self.head.next
        self.remove(first)
        return first

    # return the length of the list, time complexity O(1)
    def size(self):
        return self._size
    

class LRUCache:
    def __init__(self, capacity: int):
        # key -> Node(key, val)
        self.map = {}
        # Node(k1, v1) <-> Node(k2, v2)...
        self.cache = DoubleList()
        # maximum capacity
        self.cap = capacity

    def get(self, key: int) -> int:
        if key not in self.map:
            return -1
        
        # promote this data to the most recently used
        self.makeRecently(key)
        return self.map[key].val

    def put(self, key: int, val: int) -> None:
        if key in self.map:
            # delete old data
            self.deleteKey(key)
            # insert the new data as the most recently used
            self.addRecently(key, val)
            return
        
        if self.cap == self.cache.size():
            # remove the least recently used element
            self.removeLeastRecently()
        # add as the most recently used element
        self.addRecently(key, val)

    def makeRecently(self, key: int):
        x = self.map[key]
        # first remove this node from the list
        self.cache.remove(x)
        # reinsert it at the end of the list
        self.cache.addLast(x)

    def addRecently(self, key: int, val: int):
        x = Node(key, val)
        # the end of the list is the most recently used element
        self.cache.addLast(x)
        # don't forget to add the key mapping in the map
        self.map[key] = x

    def deleteKey(self, key: int):
        x = self.map[key]
        # remove from the list
        self.cache.remove(x)
        # remove from the map
        self.map.pop(key)

    def removeLeastRecently(self):
        # the first element at the head of the list is the least recently used
        deletedNode = self.cache.removeFirst()
        # also don't forget to remove its key from the map
        deletedKey = deletedNode.key
        self.map.pop(deletedKey)

// Doubly linked list node
type Node struct {
    key, val int
    next, prev *Node
}

// Doubly linked list
type DoubleList struct {
    // Head and tail dummy nodes
    head, tail *Node
    // Number of elements in the list
    size int
}

func NewNode(k, v int) *Node {
    return &Node{key: k, val: v}
}

func NewDoubleList() *DoubleList {
    // Initialize the data of the doubly linked list
    head := NewNode(0, 0)
    tail := NewNode(0, 0)
    head.next = tail
    tail.prev = head
    return &DoubleList{head: head, tail: tail, size: 0}
}

// Add node x at the end of the list, time complexity O(1)
func (this *DoubleList) AddLast(x *Node) {
    x.prev = this.tail.prev
    x.next = this.tail
    this.tail.prev.next = x
    this.tail.prev = x
    this.size++
}

// Remove node x from the list (x must exist)
// Since it is a doubly linked list and the target Node is given, time complexity O(1)
func (this *DoubleList) Remove(x *Node) {
    x.prev.next = x.next
    x.next.prev = x.prev
    this.size--
}

// Remove the first node in the list and return it, time complexity O(1)
func (this *DoubleList) RemoveFirst() *Node {
    if this.head.next == this.tail {
        return nil
    }
    first := this.head.next
    this.Remove(first)
    return first
}

// Return the length of the list, time complexity O(1)
func (this *DoubleList) Size() int {
    return this.size
}

type LRUCache struct {
    // key -> Node(key, val)
    _map map[int]*Node
    // Node(k1, v1) <-> Node(k2, v2)...
    cache *DoubleList
    // Maximum capacity
    cap int
}

func Constructor(capacity int) LRUCache {
    return LRUCache{
        _map:  make(map[int]*Node),
        cache: NewDoubleList(),
        cap:   capacity,
    }
}

func (this *LRUCache) Get(key int) int {
    if _, ok := this._map[key]; !ok {
        return -1
    }
    // Promote this data to the most recently used
    this.makeRecently(key)
    return this._map[key].val
}

func (this *LRUCache) Put(key, val int) {
    if _, ok := this._map[key]; ok {
        // Delete the old data
        this.deleteKey(key)
        // The newly inserted data is the most recently used
        this.addRecently(key, val)
        return
    }

    if this.cap == this.cache.Size() {
        // Remove the least recently used element
        this.removeLeastRecently()
    }
    // Add as the most recently used element
    this.addRecently(key, val)
}

func (this *LRUCache) makeRecently(key int) {
    x := this._map[key]
    // First remove this node from the list
    this.cache.Remove(x)
    // Re-insert it at the end of the list
    this.cache.AddLast(x)
}

func (this *LRUCache) addRecently(key, val int) {
    x := NewNode(key, val)
    // The end of the list is the most recently used element
    this.cache.AddLast(x)
    // Don't forget to add the key mapping in the map
    this._map[key] = x
}

func (this *LRUCache) deleteKey(key int) {
    x := this._map[key]
    // Remove from the list
    this.cache.Remove(x)
    // Remove from the map
    delete(this._map, key)
}

func (this *LRUCache) removeLeastRecently() {
    // The first element at the head of the list is the least recently used
    deletedNode := this.cache.RemoveFirst()
    // Also don't forget to remove its key from the map
    deletedKey := deletedNode.key
    delete(this._map, deletedKey)
}

javascript

// Doubly linked list node
function Node(k, v) {
    this.key = k;
    this.val = v;
    this.next = null;
    this.prev = null;
}

// Doubly linked list
function DoubleList() {
    // Head and tail dummy nodes
    this.head = new Node(0, 0);
    this.tail = new Node(0, 0);
    // Number of elements in the list
    this._size = 0;

    // Initialize the doubly linked list data
    this.head.next = this.tail;
    this.tail.prev = this.head;
}

// Add node x to the end of the list, time O(1)
DoubleList.prototype.addLast = function(x) {
    x.prev = this.tail.prev;
    x.next = this.tail;
    this.tail.prev.next = x;
    this.tail.prev = x;
    this._size++;
};

// Remove the node x from the list (x must exist)
// Since it's a doubly linked list and the target Node is given, time O(1)
DoubleList.prototype.remove = function(x) {
    x.prev.next = x.next;
    x.next.prev = x.prev;
    this._size--;
};

// Remove the first node in the list and return it, time O(1)
DoubleList.prototype.removeFirst = function() {
    if (this.head.next === this.tail) {
        return null;
    }
    var first = this.head.next;
    this.remove(first);
    return first;
};

// Return the length of the list, time O(1)
DoubleList.prototype.size = function() {
    return this._size;
};

var LRUCache = function(capacity) {
    // key -> Node(key, val)
    this.map = new Map();
    // Node(k1, v1) <-> Node(k2, v2)...
    this.cache = new DoubleList();
    // maximum capacity
    this.cap = capacity;
};

LRUCache.prototype.get = function(key) {
    if (!this.map.has(key)) {
        return -1;
    }
    // Promote this data to be the most recently used
    this.makeRecently(key);
    return this.map.get(key).val;
};

LRUCache.prototype.put = function(key, val) {
    if (this.map.has(key)) {
        // Remove the old data
        this.deleteKey(key);
        // The newly inserted data is the most recently used data
        this.addRecently(key, val);
        return;
    }

    if (this.cap === this.cache.size()) {
        // Remove the least recently used element
        this.removeLeastRecently();
    }
    // Add as the most recently used element
    this.addRecently(key, val);
};

LRUCache.prototype.makeRecently = function(key) {
    var x = this.map.get(key);
    // First remove this node from the list
    this.cache.remove(x);
    // Reinsert it at the end of the list
    this.cache.addLast(x);
};

LRUCache.prototype.addRecently = function(key, val) {
    var x = new Node(key, val);
    // The end of the list is the most recently used element
    this.cache.addLast(x);
    // Don't forget to add the key mapping in the map
    this.map.set(key, x);
};

LRUCache.prototype.deleteKey = function(key) {
    var x = this.map.get(key);
    // Remove from the list
    this.cache.remove(x);
    // Remove from the map
    this.map.delete(key);
};

LRUCache.prototype.removeLeastRecently = function() {
    // The first element at the head of the list is the least recently used
    var deletedNode = this.cache.removeFirst();
    // Also don't forget to remove its key from the map
    var deletedKey = deletedNode.key;
    this.map.delete(deletedKey);
};

You can also use Java's built-in LinkedHashMap or MyLinkedHashMap from Hands-on Implementation of Hash-Linked List to implement the LRU algorithm, with the logic remaining exactly the same.

class LRUCache {
    int cap;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();
    public LRUCache(int capacity) { 
        this.cap = capacity;
    }
    
    public int get(int key) {
        if (!cache.containsKey(key)) {
            return -1;
        }
        // make the key recently used
        makeRecently(key);
        return cache.get(key);
    }
    
    public void put(int key, int val) {
        if (cache.containsKey(key)) {
            // modify the value of the key
            cache.put(key, val);
            // make the key recently used
            makeRecently(key);
            return;
        }
        
        if (cache.size() >= this.cap) {
            // the head of the list is the least recently used key
            int oldestKey = cache.keySet().iterator().next();
            cache.remove(oldestKey);
        }
        // add the new key to the end of the list
        cache.put(key, val);
    }
    
    private void makeRecently(int key) {
        int val = cache.get(key);
        // remove the key and re-insert it at the end
        cache.remove(key);
        cache.put(key, val);
    }
}

At this point, the LRU algorithm is no longer a mystery. For more problems related to data structure design, refer to Classic Exercises in Data Structure Design.

Related Problems

You can install my Chrome extension then open the link.

LeetCode	Difficulty