Trick: Traverse Binary Tree with Stack

labuladongOriginalAbout 4239 words

Prerequisites

Before reading this article, you need to learn:

This Article is for Extension Only

Usually, we use recursive or level-order traversal to handle binary trees, which is enough for most problems.

This article introduces how to use a stack to traverse a binary tree iteratively. This is basically simulating recursion with a stack. In other problems on this site, you don't need this, and interviewers almost never require you to write this kind of code.

So, this article is just for expanding your thinking. You don't have to master it. If you're not interested, you can skip it.

DFS/BFS Traversal of Binary Tree explains recursive and level-order traversal of binary trees. These two methods are the simplest and most practical.

Some readers asked how to change the recursive preorder, inorder, and postorder frameworks to iterative ones. I used to memorize some code templates for iterative preorder, inorder, and postorder traversal. They are short and easy to remember, but not very flexible.

Not very flexible means these templates are only for "returning the preorder/inorder/postorder traversal result of a binary tree in an iterative way". The function signature is like this and returns a list of TreeNode:

java

List<TreeNode> traverse(TreeNode root);

cpp

vector<TreeNode*> traverse(TreeNode* root);

python

def traverse(root: TreeNode) -> List[TreeNode]:

func traverse(root *TreeNode) []*TreeNode

javascript

var traverse = function(root) {
};

If you have some harder problems, such as Lowest Common Ancestor or Maximum Key Sum of BST Subtree, and want to change the recursive solution to an iterative one, these templates won't help.

What I want is a universal template, which can turn any recursive binary tree algorithm into an iterative one.

In other words, a recursive framework for binary trees like this:

java

void traverse(TreeNode root) {
    if (root == null) return;
    // the position of preorder traversal code
    traverse(root.left);
    // the position of inorder traversal code
    traverse(root.right);
    // the position of postorder traversal code
}

cpp

void traverse(TreeNode* root) {
    if (root == NULL) return;
    // the position of preorder traversal code
    traverse(root->left);
    // the position of inorder traversal code
    traverse(root->right);
    // the position of postorder traversal code
}

python

def traverse(root):
    if not root:
        return
    # the position of preorder traversal code
    traverse(root.left)
    # the position of inorder traversal code
    traverse(root.right)
    # the position of postorder traversal code

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // the position of pre-order traversal code
    traverse(root.Left)
    // the position of in-order traversal code
    traverse(root.Right)
    // the position of post-order traversal code
}

javascript

var traverse = function(root) {
    if (root === null) return;
    // the position of preorder traversal code
    traverse(root.left);
    // the position of inorder traversal code
    traverse(root.right);
    // the position of postorder traversal code
};

The iterative framework should also have positions for code in the preorder, inorder, and postorder:

java

void traverse(TreeNode root) {
    while (...) {
        if (...) {
          // the position of preorder traversal code
        }
        if (...) {
          // the position of inorder traversal code
        }
        if (...) {
          // the position of postorder traversal code
        }
    }
}

cpp

void traverse(TreeNode* root) {
    while (...) {
        if (...) {
          // the position of preorder traversal code
        }
        if (...) {
          // the position of inorder traversal code
        }
        if (...) {
          // the position of postorder traversal code
        }
    }
}

python

def traverse(root: TreeNode):
    while (...):
        if (...):
          # code position for pre-order traversal
        if (...):
          # code position for in-order traversal
        if (...):
          # code position for post-order traversal

func traverse(root *TreeNode) {
    for .... {
        if ... {
            // the position of preorder traversal code
        }
        if ... {
            // the position of inorder traversal code
        }
        if ... {
            // the position of postorder traversal code
        }
    }
}

javascript

var traverse = function(root) {
    while (...) {
        if (...) {
          // the position of preorder traversal code
        }
        if (...) {
          // the position of inorder traversal code
        }
        if (...) {
          // the position of postorder traversal code
        }
    }
}

If I want to change a recursive solution to an iterative one, I can directly copy the code for preorder, inorder, and postorder into the iterative framework. It will work and give the correct result.

In theory, all recursive algorithms can be changed to iterative ones using a stack, because computers use stacks to execute recursive functions.

So, this article will use a stack to simulate recursion and summarize a general iterative traversal framework for binary trees.

Changing Recursive Framework to Iterative

According to Binary Tree Core Ideas (Summary), in the recursive framework for binary trees, the preorder, inorder, and postorder positions are special time points:

Preorder code runs when you just reach the current node root, before traversing root's left or right subtree.
Inorder code runs after finishing the left subtree of root, just before starting to traverse root's right subtree.
Postorder code runs after finishing the whole subtree rooted at the current node root.

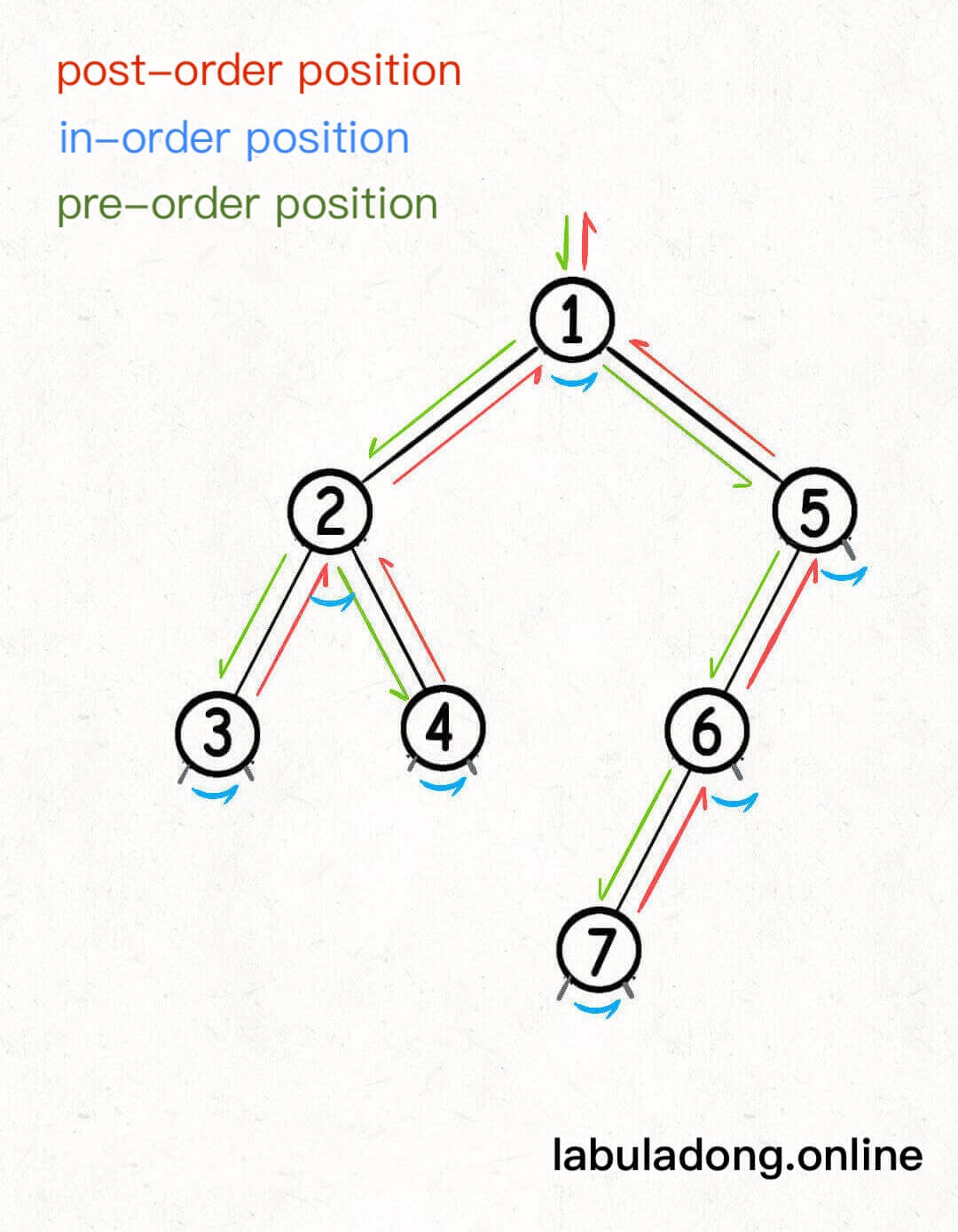
Looking at the code, this is easy to understand:

Trick: Traverse Binary Tree with Stack

Changing Recursive Framework to Iterative

Iterative Code Framework