How to Implement a Calculator
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 224. Basic Calculator | 🔴 |
| 227. Basic Calculator II | 🟠 |
| 772. Basic Calculator III🔒 | 🔴 |
The calculator we want to build will have these features:
You input a string. It can have
+ - * /, numbers, parentheses, and spaces. Your algorithm returns the result.The calculation follows the normal math rules. Parentheses have the highest priority. Multiply and divide come before add and subtract.
Division is integer division. No matter positive or negative, round toward zero (5/2=2, -5/2=-2).
You can assume the input is always valid. There will not be integer overflow, and no division by zero.
For example, if you input this string, the algorithm will return 9:
3 * (2 - 6 / (3 - 7))
= 3 * (2 - 6 / (-4))
= 3 * (2 - (-1))
= 9As you can see, this is already very close to a real calculator. Although we all have used calculators before, if you think about how to implement its algorithm, it is not that easy:
To handle parentheses, you must calculate the innermost ones first, then simplify step by step. Even when doing it by hand, it's easy to make mistakes. Writing it as an algorithm is even harder.
You must handle multiplication and division before addition and subtraction. This is not so hard for kids to learn, but it is tricky for computers.
You need to deal with spaces. For better readability, we often put spaces between numbers and operators. But during calculation, these spaces should be ignored.
I remember many data structure textbooks use calculators as an example when explaining stacks. But honestly, the explanation is not good. Many future computer scientists may have been discouraged by such a simple data structure.
So in this article, let's talk about how to build a fully functional calculator. The key is to break down the problem step by step, solve each part one by one. With a few simple algorithm rules, you can handle very complex calculations. I believe this way of thinking can help you solve many hard problems.
Let's start by breaking down the problem, beginning with the simplest one.
1. String to Integer
Yes, this is a simple problem. First, tell me how to convert a string that represents a positive integer into an int type?
String s = "458";
int n = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
n = 10 * n + (c - '0');
}
// n is now equal to 458std::string s = "458";
int n = 0;
for (int i = 0; i < s.length(); i++) {
char c = s[i];
n = 10 * n + (c - '0');
}
// n is now equal to 458s = "458"
n = 0
for i in range(len(s)):
c = s[i]
n = 10 * n + (ord(c) - ord('0'))
# n is now equal to 458s := "458"
n := 0
for i := 0; i < len(s); i++ {
c := int(s[i] - '0')
n = 10*n + c
}
// n is now equal to 458var s = "458";
var n = 0;
for (var i = 0; i < s.length; i++) {
var c = s.charAt(i);
n = 10 * n + (c.charCodeAt(0) - '0'.charCodeAt(0));
}
// n is now equal to 458This is very simple and a common routine. But even for such a simple problem, there is a pitfall: You cannot remove the parentheses in (c - '0'), or it may cause integer overflow.
Because the variable c is an ASCII code. Without parentheses, addition may happen before subtraction. If s is close to INT_MAX, this can cause overflow. So, use parentheses to make sure subtraction happens first.
2. Handling Addition and Subtraction
Now, let's move on. If the input formula only contains addition and subtraction, and there are no spaces, how can you calculate the result? Let's use the string 1-12+3 as an example:
Add a default
+sign before the first number, so it becomes+1-12+3.Combine each operator and number into a pair. For example:
+1,-12,+3. Convert them to numbers, then put them into a stack.Add up all the numbers in the stack. The sum is the result of the formula.
Let's look at the code and a picture to make it clear:
int calculate(String s) {
Stack<Integer> stk = new Stack<>();
// record the numbers in the expression
int num = 0;
// record the sign before num, initialize as +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
// if it's a digit, continuously read it into num
if (Character.isDigit(c)) {
num = 10 * num + (c - '0');
}
// if it's not a digit, it means we encountered the
// next sign or the end of the expression
// then the previous number and sign should be pushed into the stack
if (c == '+' || c == '-' || i == s.length() - 1) {
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
}
// update the sign to the current one, reset num to zero
sign = c;
num = 0;
}
}
// sum up all the results in the stack to get the answer
int res = 0;
while (!stk.isEmpty()) {
res += stk.pop();
}
return res;
}int calculate(string s) {
stack<int> stk;
// record the numbers in the expression
int num = 0;
// record the sign before num, initialize as +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s[i];
// if it's a digit, continuously read into num
if (isdigit(c)) {
num = 10 * num + (c - '0');
}
// if it's not a digit, it means encountering the next sign or the end of the expression
// then the previous number and sign should be stored in the stack
if (c == '+' || c == '-' || i == s.length() - 1) {
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
}
// update the sign to the current sign, reset the number to zero
sign = c;
num = 0;
}
}
// sum all results in the stack to get the answer
int res = 0;
while (!stk.empty()) {
res += stk.top();
stk.pop();
}
return res;
}def calculate(s):
stk = []
# record the numbers in the formula
num = 0
# record the sign before num, initialized to +
sign = '+'
for i in range(len(s)):
c = s[i]
# if it's a digit, read it continuously into num
if c.isdigit():
num = 10 * num + int(c)
# if it's not a digit, then it means we've
# encountered the next sign or the end of the formula
# then the previous number and sign should be stored in the stack
if c == '+' or c == '-' or i == len(s) - 1:
if sign == '+':
stk.append(num)
elif sign == '-':
stk.append(-num)
# update the sign to the current sign and reset the number to zero
sign = c
num = 0
# the answer is the sum of all results in the stack
res = 0
while stk:
res += stk.pop()
return resfunc calculate(s string) int {
// record the number in the expression
var num int
// final result
var res int
// record the sign before num, initialize to +
var sign int = 1
// stack initialization
stk := stack.New()
// start traversing s in order
for i := 0; i < len(s); i++ {
// if it's a digit, continuously read into num
if isDigit(s[i]) {
num = 10*num + int(s[i]-'0')
}
// if it's not a digit, it means encountering the next sign or the end of the expression
// then the previous number and sign should be stored in the stack
if s[i] == '+' || s[i] == '-' || i == len(s)-1 {
// store the number and sign in the stack
if sign == 1 {
stk.Push(num)
} else if sign == -1 {
stk.Push(-num)
}
// update the sign to the current sign, reset the number to zero
num = 0
if s[i] == '+' {
sign = 1
} else if s[i] == '-' {
sign = -1
}
}
}
// sum all the results in the stack to get the answer
for stk.Len() != 0 {
res += stk.Pop().(int)
}
// return the result
return res
}
// helper function, determine if a character is a digit
func isDigit(n byte) bool {
if '0' <= n && n <= '9' {
return true
}
return false
}var calculate = function(s) {
// declare an array to replace the original Java stack
var stk = [];
// record the numbers in the formula
var num = 0;
// record the sign before num, initialized as +
var sign = '+';
for (var i = 0; i < s.length; i++) {
var c = s.charAt(i);
// if it's a number, continuously read into num
if (!isNaN(c)) {
num = 10 * num + (c - '0');
}
// if it's not a number, it means we encountered
// the next sign, or the end of the formula
// then the previous number and sign should be stored into the stack
if (c === '+' || c === '-' || i === s.length - 1) {
switch(sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
}
// update the sign to the current sign, and reset the number to zero
sign = c;
num = 0;
}
}
// summing all the results in the stack gives the answer
var res = 0;
while (stk.length !== 0) {
res += stk.pop();
}
return res;
}Maybe the part with the switch statement is a bit hard to understand. i scans from left to right, and sign and num follow it. When s[i] meets an operator, here's what happens:
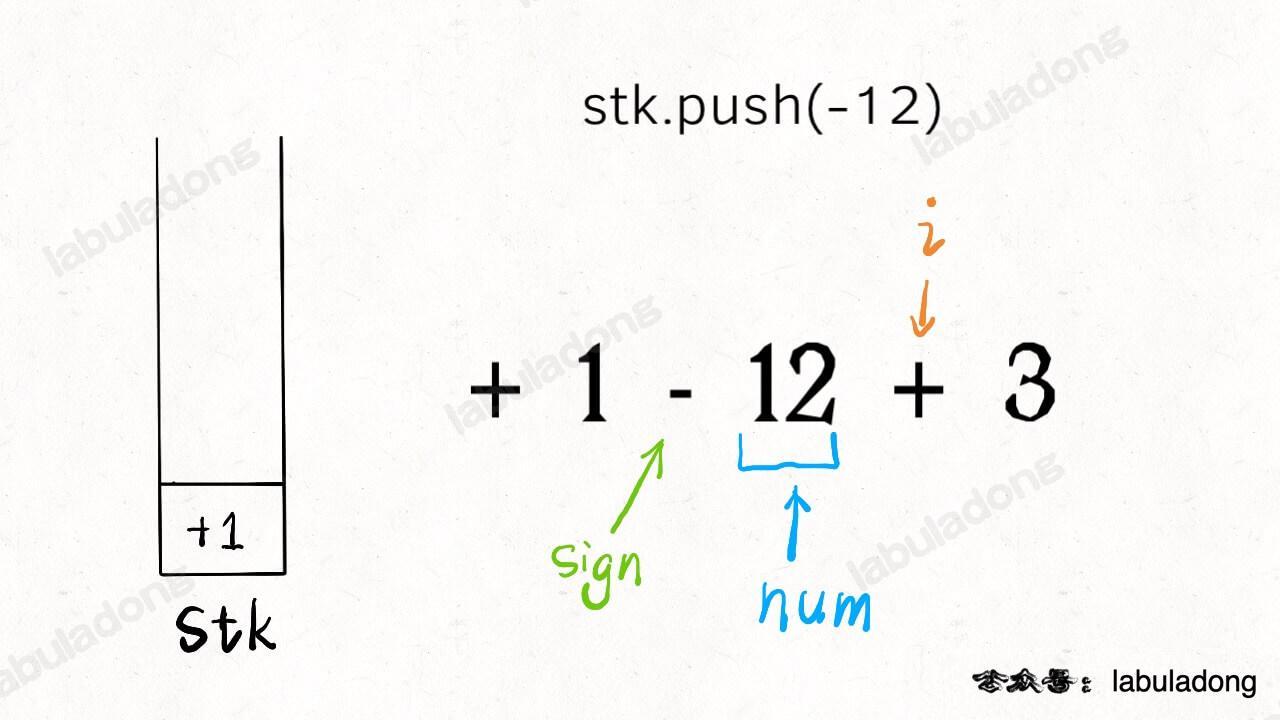
Now, use sign to decide if the number is positive or negative, put it into the stack, then update sign and reset num to get ready for the next pair.
Also, not only when you meet a new operator should you push to the stack. When i reaches the end of the string (i == s.size() - 1), you should also put the last number into the stack for the final calculation.
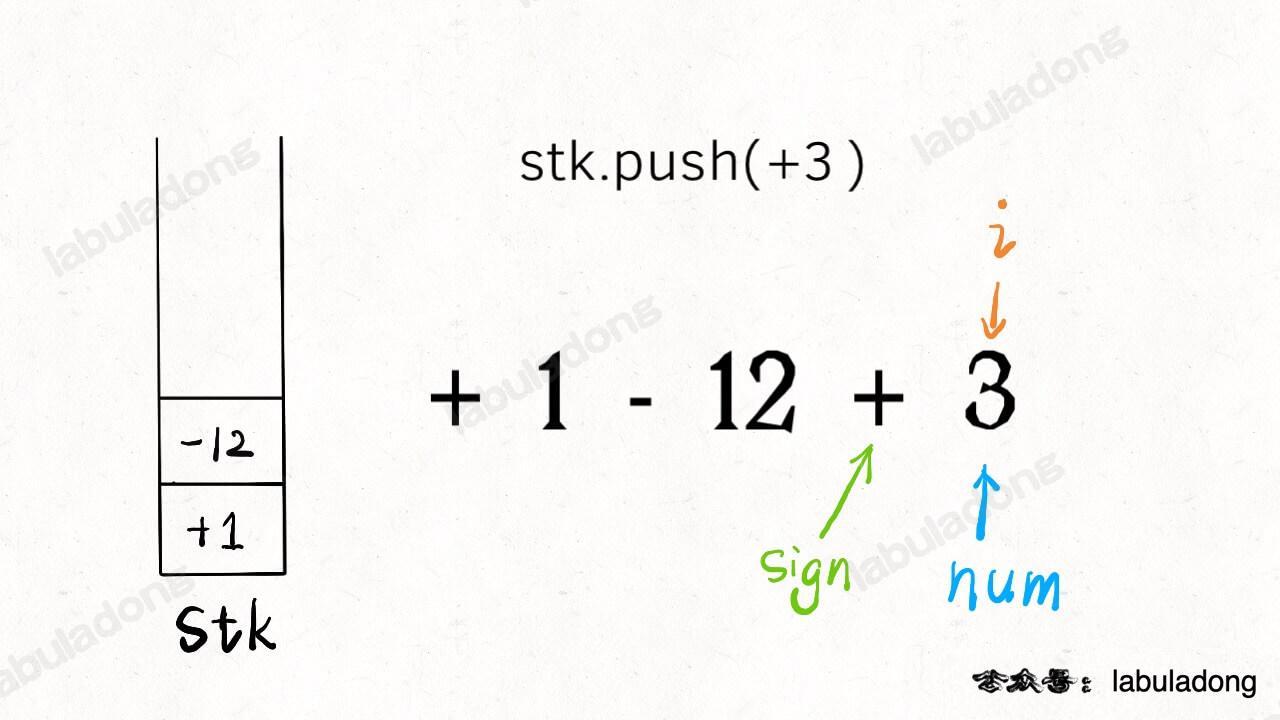
That's it. This is the algorithm for compact addition and subtraction strings. Make sure you understand this part. The next steps just change this base framework a bit.
3. Handling Multiplication and Division
The idea is almost the same as just handling addition and subtraction. Let's use the string 2-3*4+5 as an example. The core idea is still to break the string into pairs of symbols and numbers.
For example, this can be split into +2, -3, *4, +5. Before, we didn't handle multiplication and division. That's easy. Everything else stays the same. Just add the cases for multiplication and division in the switch part:
int calculate(String s) {
Stack<Integer> stk = new Stack<>();
// record the numbers in the formula
int num = 0;
// record the sign before num, initialized as +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '+' || c == '-' || c == '/' || c == '*' || i == s.length() - 1) {
int pre;
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
// just take out the previous number and perform corresponding operation
case '*':
pre = stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.pop();
stk.push(pre / num);
break;
}
// update the sign to the current sign, reset the number to zero
sign = c;
num = 0;
}
}
// sum up all the results in the stack to get the answer
int res = 0;
while (!stk.isEmpty()) {
res += stk.pop();
}
return res;
}int calculate(string s) {
stack<int> stk;
// record the numbers in the formula
int num = 0;
// record the sign before num, initialized to +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s[i];
if (isdigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '+' || c == '-' || c == '/' || c == '*' || i == s.length() - 1) {
int pre;
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
// just take out the previous number for the corresponding operation
case '*':
pre = stk.top(); stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.top(); stk.pop();
stk.push(pre / num);
break;
}
// update the sign to the current sign, reset the number to zero
sign = c;
num = 0;
}
}
// summing up all the results in the stack gives the answer
int res = 0;
while (!stk.empty()) {
res += stk.top(); stk.pop();
}
return res;
}def calculate(s: str) -> int:
stk = []
# record the numbers in the equation
num = 0
# record the sign before num, initialized as +
sign = "+"
for i in range(len(s)):
if s[i].isdigit():
num = 10 * num + int(s[i])
# encounter +,-,*,/ or reach the end
if s[i] in "+-*/" or i == len(s) - 1:
if sign == "+":
stk.append(num)
elif sign == "-":
stk.append(-num)
# just take out the previous number and perform the corresponding operation
elif sign == "*":
stk[-1] *= num
else:
# encounter division sign, need to take out the
# previous number and perform division
stk[-1] = int(stk[-1] / num)
# update the sign to the current sign, reset the number to zero
sign = s[i]
num = 0
# sum all results in the stack to get the answer
return sum(stk)func calculate(s string) int {
// initialize stack stk
stk := make([]int, 0)
// record numbers in the expression
num := 0
// record the sign before num, initialized to +
sign := '+'
for i, c := range s {
if unicode.IsDigit(c) {
num = 10*num + int(c-'0')
}
if c=='+' || c=='-' || c=='/' || c=='*' || i==len(s)-1 {
var pre int
switch sign {
case '+':
// if the sign is +, push the number onto the stack
stk = append(stk, num)
case '-':
// if the sign is -, push the negated number onto the stack
stk = append(stk, -num)
case '*':
// if the sign is *, pop the top element of the stack, multiply it by
// the current number, and push the result back onto the stack
pre = stk[len(stk)-1]
stk = stk[:len(stk)-1]
stk = append(stk, pre*num)
case '/':
// if the sign is /, pop the top element of the stack, divide it by
// the current number, and push the result back onto the stack
pre = stk[len(stk)-1]
stk = stk[:len(stk)-1]
stk = append(stk, pre/num)
}
// update the sign to the current sign, and reset the number to 0
sign = rune(c)
num = 0
}
}
// sum all the results in the stack to get the answer
res := 0
for _, v := range stk {
res += v
}
return res
}var calculate = function(s) {
var stack = [];
// record the numbers in the formula
var num = 0;
// record the sign before num, initialized to +
var sign = '+';
for (var i = 0; i < s.length; i++) {
var c = s[i];
if (!isNaN(c)) {
num = 10 * num + (c - '0');
}
if (c === '+' || c === '-' || c === '/' || c === '*' || i === s.length - 1) {
var pre;
switch (sign) {
// just take out the previous number and perform the corresponding operation
case '+':
stack.push(num); break;
case '-':
stack.push(-num); break;
case '*':
pre = stack.pop();
stack.push(pre * num);
break;
case '/':
pre = stack.pop();
stack.push(Math.trunc(pre / num));
break;
}
// update the sign to the current sign, and reset the number to zero
sign = c;
num = 0;
}
}
// sum all the results in the stack to get the answer
var res = 0;
while (stack.length !== 0) {
res += stack.pop();
}
return res;
};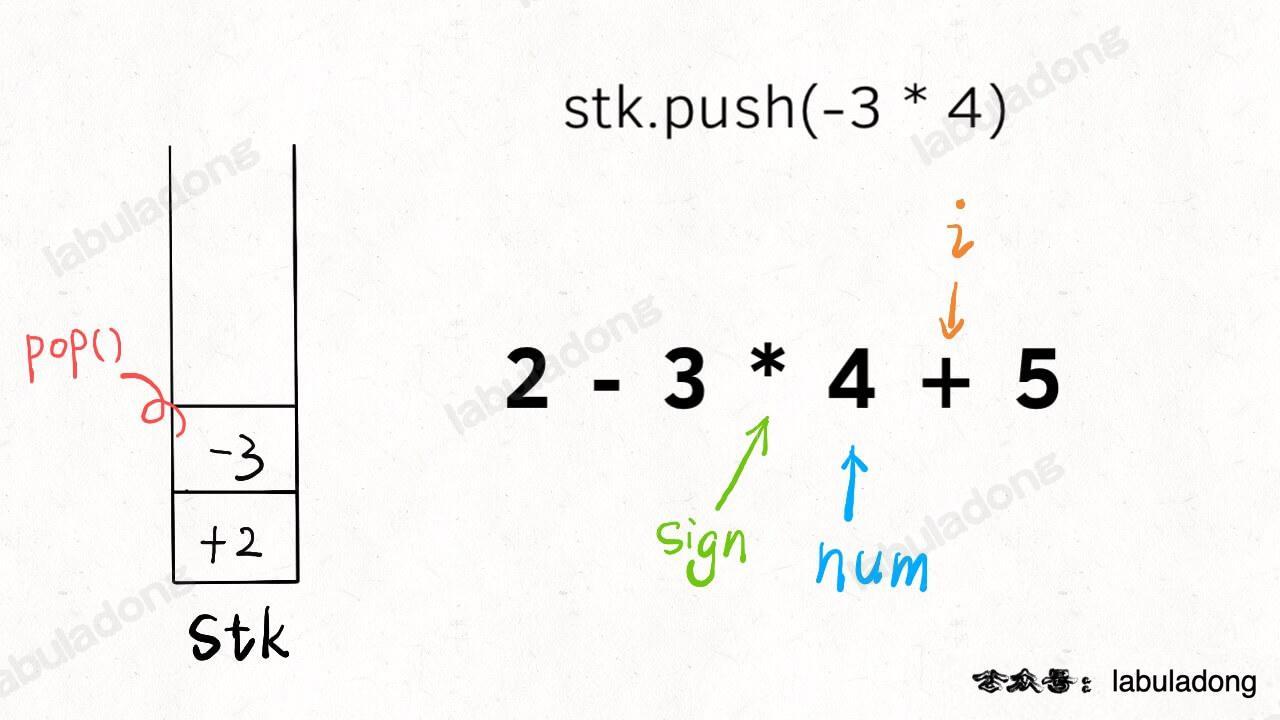
Multiplication and division have higher priority than addition and subtraction. This means you combine them with the top number in the stack, while addition and subtraction just push their number into the stack.
Now let's think about spaces in the string. In our code, there is no need to handle spaces specially. Look at the if conditions: if the character c is a space, we just skip it.
Now, our algorithm can calculate addition, subtraction, multiplication, and division correctly, and automatically ignores spaces. The last step is to make the algorithm handle parentheses correctly.