Binary Search Tree in Action (Construction)
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 95. Unique Binary Search Trees II | 🟠 |
| 96. Unique Binary Search Trees | 🟠 |
Prerequisites
Before reading this article, you need to learn:
Previously, I wrote two articles on step-by-step solving of BST algorithm problems. The first article discussed the significance of in-order traversal for BSTs, and the second article covered basic operations of BSTs.
This article is the third in the step-by-step solving series on BSTs, gradually explaining two problems on how to calculate all valid BSTs.
The first problem is LeetCode problem 96, "Unique Binary Search Trees":
96. Unique Binary Search Trees | LeetCode | 🟠
Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.
Example 1:
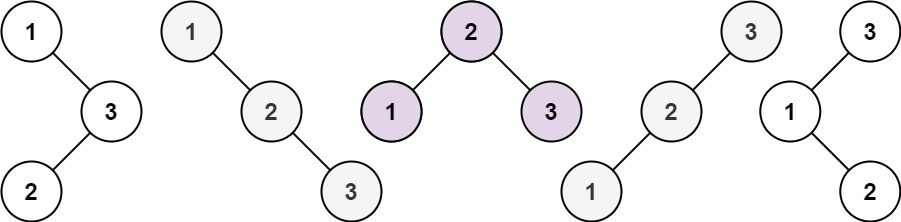
Input: n = 3 Output: 5
Example 2:
Input: n = 1 Output: 1
Constraints:
1 <= n <= 19
The function signature is as follows:
int numTrees(int n);int numTrees(int n);def numTrees(n: int) -> int:func numTrees(n int) int {}var numTrees = function(n) {
};This is a classic brute-force problem. What method can correctly enumerate the number of valid Binary Search Trees (BSTs)?
We have mentioned before that "brute-force" should not be underestimated; it is a seemingly simple task that requires considerable technical skill. The key is to ensure that we do not miss any counts, nor count extra. How do you approach this?
As discussed in the previous article Hand-in-Hand Binary Tree Training Part 1, the key to binary tree algorithms lies in defining what the root node needs to do. In fact, for BSTs, which are a special type of binary tree, the core idea remains the same.