Binary Search Tree in Action (Basic Operations)

labuladongOriginalAbout 4880 words

This article will resolve

LeetCode	Difficulty
450. Delete Node in a BST	🟠
700. Search in a Binary Search Tree	🟢
701. Insert into a Binary Search Tree	🟠
98. Validate Binary Search Tree	🟠

Prerequisite

Before reading this article, you should first learn:

In the previous article Binary Search Tree Basics (Features), we introduced the basic features of BST and used the "in-order traversal is sorted" property to solve some problems. In this article, we'll implement the basic operations of BST: checking if a BST is valid, inserting, deleting, and searching. Among these, "deleting" and "checking validity" are a bit more complex.

The basic operations of BST mainly rely on the "left smaller, right bigger" property. This allows us to do binary search-like operations in the tree, making it very efficient to find an element. For example, the following is a valid binary search tree:

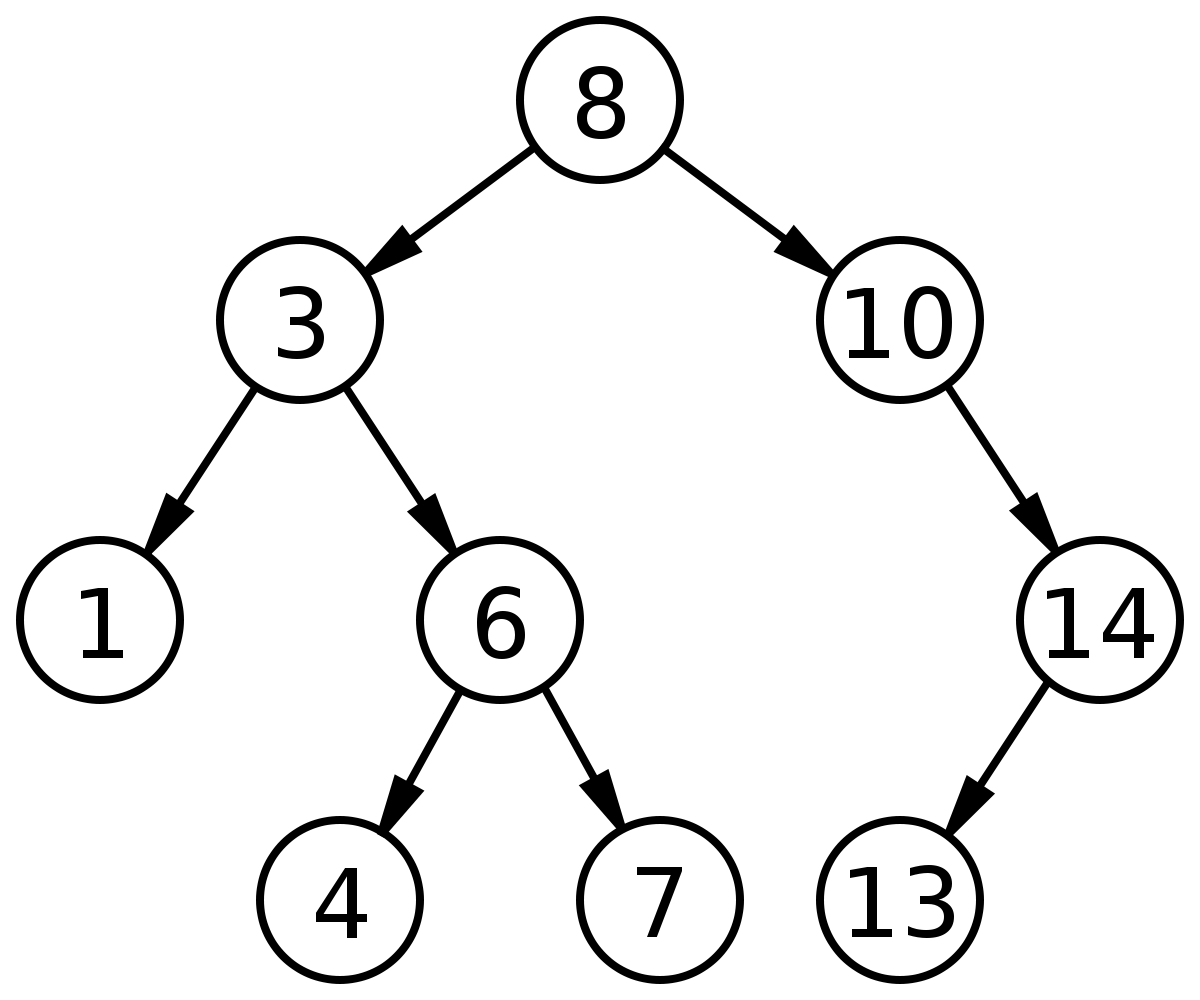
For BST problems, you will often see code logic like this:

java

void BST(TreeNode root, int target) {
    if (root.val == target)
        // found the target, do something
    if (root.val < target) 
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

cpp

void BST(TreeNode* root, int target) {
    if (root->val == target)
        // found the target, do something
    if (root->val < target) 
        BST(root->right, target);
    if (root->val > target)
        BST(root->left, target);
}

python

def BST(root: TreeNode, target: int) -> None:
    if root.val == target:
        # target found, do something
    if root.val < target:
        BST(root.right, target)
    if root.val > target:
        BST(root.left, target)

func BST(root *TreeNode, target int) {
    if root.Val == target {
        // found the target, do something
    }
    if root.Val < target {
        BST(root.Right, target)
    }
    if root.Val > target {
        BST(root.Left, target)
    }
}

javascript

var BST = function(root, target) {
    if (root.val === target) {
        // found the target, do something
    }
    if (root.val < target) { 
        BST(root.right, target);
    }
    if (root.val > target) {
        BST(root.left, target);
    }
};

This code framework is similar to the usual binary tree traversal, just using the BST "left smaller, right bigger" feature. Next, let's see how the basic operations on BST are implemented.

1. Check if a BST is Valid

LeetCode Problem 98 "Validate Binary Search Tree" asks you to check if a given BST is valid:

98. Validate Binary Search Tree | LeetCode | 🟠

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

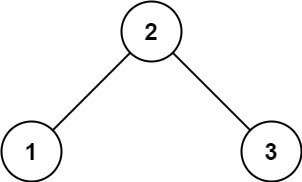
Input: root = [2,1,3]
Output: true

Example 2:

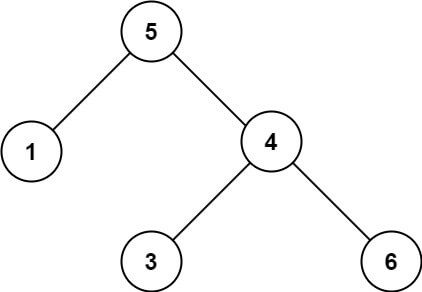
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Constraints:

The number of nodes in the tree is in the range [1, 10⁴].
-2³¹ <= Node.val <= 2³¹ - 1

The problem is from LeetCode 98. Validate Binary Search Tree.

Be careful, there is a trap here. According to the BST property, every node should be compared with its left and right children to check if it is valid. It seems you might write code like this:

java

boolean isValidBST(TreeNode root) {
    if (root == null) return true;
    // the left side of the root should be smaller
    if (root.left != null && root.left.val >= root.val)
        return false;
    // the right side of the root should be larger
    if (root.right != null && root.right.val <= root.val)
        return false;

    return isValidBST(root.left)
        && isValidBST(root.right);
}

cpp

bool isValidBST(TreeNode* root) {
    if (root == nullptr) return true;
    // the left side of root should be smaller
    if (root->left != nullptr && root->left->val >= root->val)
        return false;
    // the right side of root should be bigger
    if (root->right != nullptr && root->right->val <= root->val)
        return false;

    return isValidBST(root->left)
        && isValidBST(root->right);
}

python

def isValidBST(root: TreeNode) -> bool:
    if root is None:
        return True
    # the left of root should be smaller
    if root.left is not None and root.left.val >= root.val:
        return False
    # the right of root should be larger
    if root.right is not None and root.right.val <= root.val:
        return False

    return isValidBST(root.left) and isValidBST(root.right)

func isValidBST(root *TreeNode) bool {
    if root == nil {
        return true
    }
    // the left side of root should be smaller
    if root.Left != nil && root.Left.Val >= root.Val {
        return false
    }
    // the right side of root should be larger
    if root.Right != nil && root.Right.Val <= root.Val {
        return false
    }

    return isValidBST(root.Left)
        && isValidBST(root.Right)
}

javascript

var isValidBST = function(root) {
    if (root === null) return true;
    // the left side of the root should be smaller
    if (root.left !== null && root.left.val >= root.val)
        return false;
    // the right side of the root should be larger
    if (root.right !== null && root.right.val <= root.val)
        return false;

    return isValidBST(root.left)
        && isValidBST(root.right);
}

But this algorithm is wrong. For BST, every node must be less than all nodes in its right subtree. The following tree is not a valid BST because there is a node 8 in the left subtree of node 7, but our code would say it is valid:

The reason for the mistake is that, for each node root, the code only checks its left and right child nodes. But, by the definition of BST, the whole left subtree of root must be less than root.val, and the whole right subtree must be greater than root.val.

The problem is, for a node root, it can only directly check its children. How do we pass this constraint down to all nodes of the left and right subtree? Here is the correct code:

java

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, null, null);
    }

    // nodes in the subtree rooted at root must satisfy max.val > root.val > min.val
    boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
        // base case
        if (root == null) return true;
        // if root.val does not satisfy the constraints of max and min, it is not a valid BST
        if (min != null && root.val <= min.val) return false;
        if (max != null && root.val >= max.val) return false;
        // the maximum value in the left subtree is root.val, and
        // the minimum value in the right subtree is root.val
        return isValidBST(root.left, min, root)
                && isValidBST(root.right, root, max);
    }
}

cpp

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return _isValidBST(root, nullptr, nullptr);
    }

    // Definition: This function returns whether all nodes in the
    // subtree rooted at root satisfy max->val > root->val > min->val
    bool _isValidBST(TreeNode* root, TreeNode* min, TreeNode* max) {
        // base case
        if (root == nullptr) return true;
        // If root->val does not satisfy the constraints of max and min, it is not a valid BST
        if (min != nullptr && root->val <= min->val) return false;
        if (max != nullptr && root->val >= max->val) return false;
        // According to the definition, the maximum value of the left subtree is
        // root->val and the minimum value of the right subtree is root->val
        return _isValidBST(root->left, min, root) 
            && _isValidBST(root->right, root, max);
    }
};

python

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        return self._isValidBST(root, None, None)

    # Definition: This function returns whether all nodes in the
    # subtree rooted at `root` satisfy max.val > root.val > min.val
    def _isValidBST(self, root: TreeNode, min: TreeNode, max: TreeNode) -> bool:
        # base case
        if root is None:
            return True
        # If root.val does not comply with the constraints of max and min, it is not a valid BST
        if min is not None and root.val <= min.val:
            return False
        if max is not None and root.val >= max.val:
            return False
        # According to the definition, the maximum value of the left subtree is
        # root.val, and the minimum value of the right subtree is root.val
        return self._isValidBST(root.left, min, root) and self._isValidBST(root.right, root, max)

func isValidBST(root *TreeNode) bool {
    return _isValidBST(root, nil, nil)
}

// Definition: This function returns whether all nodes of the
// subtree rooted at root satisfy max.Val > root.Val > min.Val
func _isValidBST(root *TreeNode, min, max *TreeNode) bool {
    // base case
    if root == nil {
        return true
    }
    // If root.Val does not meet the constraints of max and min, it is not a valid BST
    if min != nil && root.Val <= min.Val {
        return false
    }
    if max != nil && root.Val >= max.Val {
        return false
    }
    // By definition, limit the maximum value of the left subtree to
    // root.Val and the minimum value of the right subtree to root.Val
    return _isValidBST(root.Left, min, root) && _isValidBST(root.Right, root, max)
}

javascript

var isValidBST = function(root) {
    return _isValidBST(root, null, null);
};

// Definition: This function returns whether all nodes in the
// subtree rooted at 'root' satisfy max.val > root.val > min.val
var _isValidBST = function(root, min, max) {
    // base case
    if (root === null) return true;
    // If root.val does not meet the constraints of max and min, it is not a valid BST
    if (min !== null && root.val <= min.val) return false;
    if (max !== null && root.val >= max.val) return false;
    // According to the definition, the maximum value of the left subtree is
    // root.val, and the minimum value of the right subtree is root.val
    return _isValidBST(root.left, min, root) 
        && _isValidBST(root.right, root, max);
};

Algorithm Visualization

We use a helper function and add extra parameters to pass down these constraints to all child nodes. This is also a useful trick in binary tree algorithms.

Search for an Element in a BST

LeetCode problem 700, "Search in a Binary Search Tree," asks you to find a node with value target in a BST. The function signature is as follows:

java

TreeNode searchBST(TreeNode root, int target);

cpp

TreeNode* searchBST(TreeNode* root, int target);

python

def searchBST(root: TreeNode, target: int) -> TreeNode:

func searchBST(root *TreeNode, target int) *TreeNode {
    // Implementation goes here
}

javascript

var searchBST = function(root, target) {}

If you are searching in a normal binary tree, you can write the code like this:

java

TreeNode searchBST(TreeNode root, int target) {
    if (root == null) return null;
    if (root.val == target) return root;
    // if the current node is not found, recursively search the left and right subtrees
    TreeNode left = searchBST(root.left, target);
    TreeNode right = searchBST(root.right, target);

    return left != null ? left : right;
}

cpp

TreeNode* searchBST(TreeNode* root, int target) {
    if (root == nullptr) return nullptr;
    if (root->val == target) return root;
    // if the current node is not found, recursively search the left and right subtrees
    TreeNode* left = searchBST(root->left, target);
    TreeNode* right = searchBST(root->right, target);
    return left != nullptr ? left : right;
}

python

def searchBST(root, target):
    if not root:
        return None
    if root.val == target:
        return root
    # if the current node is not found, recursively search the left and right subtrees
    left = searchBST(root.left, target)
    right = searchBST(root.right, target)

    return left if left else right

func searchBST(root *TreeNode, target int) *TreeNode {
    if root == nil {
        return nil
    }
    if root.val == target {
        return root
    }
    // recursively search left and right subtrees
    left := searchBST(root.left, target)
    right := searchBST(root.right, target)
    // if the target node is found in the left subtree, return
    // the left subtree; otherwise, return the right subtree
    if left != nil {
        return left
    }
    return right
}

javascript

var searchBST = function(root, target) {
    if (root == null) return null;
    if (root.val == target) return root;
    // if the current node is not found, recursively search the left and right subtrees
    let left = searchBST(root.left, target);
    let right = searchBST(root.right, target);

    return left != null ? left : right;
};

This code is correct, but it checks all nodes, which is brute-force and works for any binary tree. But how can we use the special property of BST, where the left side is smaller and the right side is larger?

It is simple. You do not need to search both sides. You can use a binary search idea: compare target with root.val. This way, you can ignore one side. Let's change the code using this idea:

java

// define: search for the node with value target in the BST rooted at root, return the node
TreeNode searchBST(TreeNode root, int target) {
    if (root == null) {
        return null;
    }
    // search in the left subtree
    if (root.val > target) {
        return searchBST(root.left, target);
    }
    // search in the right subtree
    if (root.val < target) {
        return searchBST(root.right, target);
    }
    // the current node is the target value
    return root;
}

cpp

// define: search for the node with value target in the BST rooted at root, return the node
TreeNode* searchBST(TreeNode* root, int target) {
    if (root == nullptr) {
        return nullptr;
    }
    // search in the left subtree
    if (root->val > target) {
        return searchBST(root->left, target);
    }
    // search in the right subtree
    if (root->val < target) {
        return searchBST(root->right, target);
    }
    // the current node is the target value
    return root;
}

python

# define: search for the node with value target in the BST rooted at root, return the node
def searchBST(root: TreeNode, target: int) -> TreeNode:
    # if the binary tree is empty, return directly
    if not root:
        return None
    # search in the left subtree
    if root.val > target:
        return searchBST(root.left, target)
    # search in the right subtree
    if root.val < target:
        return searchBST(root.right, target)
    # the current node is the target value
    return root

// define: search for the node with value target in the BST rooted at root, return the node
func searchBST(root *TreeNode, target int) *TreeNode {
    // if the root node is nil, return nil
    if root == nil {
        return nil
    }
    // search in the left subtree
    if root.val > target {
        return searchBST(root.left, target)
    }
    // search in the right subtree
    if root.val < target {
        return searchBST(root.right, target)
    }
    // the current node is the target value
    return root
}

javascript

// define: search for the node with value target in the BST rooted at root, return the node
var searchBST = function(root,target) {
    if (root === null) {
        return null;
    }
    // search in the left subtree
    if (root.val > target) {
        return searchBST(root.left, target);
    }
    // search in the right subtree
    if (root.val < target) {
        return searchBST(root.right, target);
    }
    // target value equals the current node, return directly
    return root;
}

Algorithm Visualization

Insert a Number into a BST

When working with data structures, you usually travel through (find) and visit (change) the nodes. For this problem, to insert a number, you first find the right position, then insert it.

BSTs usually do not have duplicate values, so you do not need to insert a value that is already in the BST. The code below assumes you will not insert a value that already exists in the BST.

In the last problem, we summarized the way to travel through a BST, which is the "find" part. Now, just add the "change" part.

If you need to change the tree, it is like building a binary tree; the function should return TreeNode, and you need to use the result from the recursive call.

LeetCode problem 701, "Insert into a Binary Search Tree," is about this:

701. Insert into a Binary Search Tree | LeetCode | 🟠

You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.

Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.

Example 1:

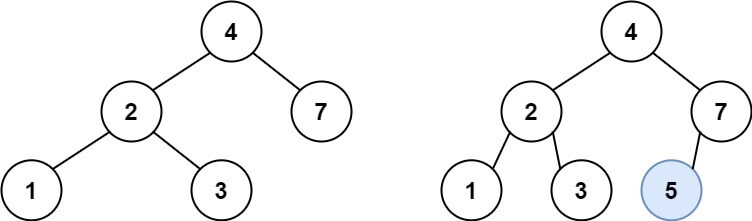
Input: root = [4,2,7,1,3], val = 5
Output: [4,2,7,1,3,5]
Explanation: Another accepted tree is: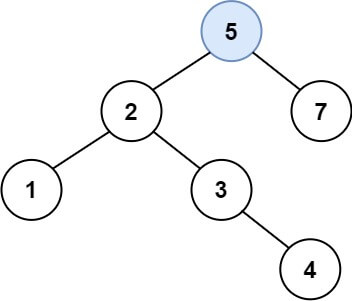

Example 2:

Input: root = [40,20,60,10,30,50,70], val = 25
Output: [40,20,60,10,30,50,70,null,null,25]

Example 3:

Input: root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
Output: [4,2,7,1,3,5]

Constraints:

The number of nodes in the tree will be in the range [0, 10⁴].
-10⁸ <= Node.val <= 10⁸
All the values Node.val are unique.
-10⁸ <= val <= 10⁸
It's guaranteed that val does not exist in the original BST.

The problem is from LeetCode 701. Insert into a Binary Search Tree.

Let's look at the solution code. You can use the comments and visual panel to help you understand:

java

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        // find the empty spot to insert the new node
        if (root == null) return new TreeNode(val);
        // if (root.val == val)
        // generally, in a bst, we don't insert an element that already exists
        if (root.val < val)
            root.right = insertIntoBST(root.right, val);
        if (root.val > val)
            root.left = insertIntoBST(root.left, val);
        return root;
    }
}

cpp

// define: insert val into the BST rooted at root, return the root of the modified BST
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr) {
            // find the empty position to insert the new node
            return new TreeNode(val);
        }

        // look for the insertion position in the right subtree
        if (root->val < val) {
            root->right = insertIntoBST(root->right, val);
        }
        // look for the insertion position in the left subtree
        if (root->val > val) {
            root->left = insertIntoBST(root->left, val);
        }
        // return root, the upper recursion will take the return value as a child node
        return root;
    }
};

python

# define: insert val into the BST rooted at root, return the root of the modified BST
class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            # find an empty spot to insert the new node
            return TreeNode(val)
        # go to the right subtree to find the insertion position
        if root.val < val:
            root.right = self.insertIntoBST(root.right, val)
        # go to the left subtree to find the insertion position
        if root.val > val:
            root.left = self.insertIntoBST(root.left, val)
        # return root, the upper level of recursion will
        # receive the return value as a child node
        return root

// define: insert val into the BST rooted at root, return the root of the modified BST
func insertIntoBST(root *TreeNode, val int) *TreeNode {
    if root == nil {
        // find the empty position to insert the new node
        return &TreeNode{Val: val}
    }
    // find the position to insert in the right subtree
    if root.Val < val {
        root.Right = insertIntoBST(root.Right, val)
    }
    // find the position to insert in the left subtree
    if root.Val > val {
        root.Left = insertIntoBST(root.Left, val)
    }
    // return root, the upper recursion will receive the return value as a child node
    return root
}

javascript

// define: insert val into the BST rooted at root, return the root of the modified BST
var insertIntoBST = function(root, val) {
    if (root === null) {
        // find the empty spot to insert the new node
        return new TreeNode(val);
    }
    // find the insertion spot in the right subtree
    if (root.val < val) {
        root.right = insertIntoBST(root.right, val);
    }
    // find the insertion spot in the left subtree
    if (root.val > val) {
        root.left = insertIntoBST(root.left, val);
    }
    // return root, the upper recursion will receive the return value as a child node
    return root;
}

Algorithm Visualization

3. Delete a Node in a BST

LeetCode Problem 450: Delete Node in a BST asks you to delete a node with value key from a BST:

450. Delete Node in a BST | LeetCode | 🟠

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

Search for a node to remove.
If the node is found, delete the node.

Example 1:

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.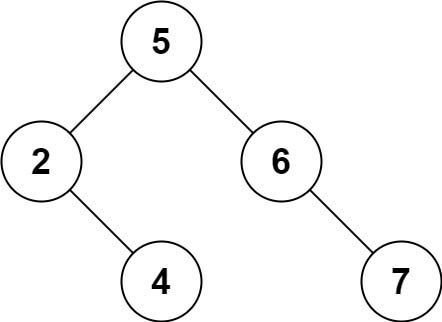

Example 2:

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 10⁴].
-10⁵ <= Node.val <= 10⁵
Each node has a unique value.
root is a valid binary search tree.
-10⁵ <= key <= 10⁵

Follow up: Could you solve it with time complexity O(height of tree)?

The problem is from LeetCode 450. Delete Node in a BST.

This problem is a bit tricky. Like insertion, you need to "find" first, then "change." Let's write the basic structure first:

java

TreeNode deleteNode(TreeNode root, int key) {
    if (root.val == key) {
        // found it, proceed to delete
    } else if (root.val > key) {
        // go to the left subtree
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        // go to the right subtree
        root.right = deleteNode(root.right, key);
    }
    return root;
}

cpp

TreeNode* deleteNode(TreeNode* root, int key) {
    if (root->val == key) {
        // found it, proceed to delete
    } else if (root->val > key) {
        // go to the left subtree
        root->left = deleteNode(root->left, key);
    } else if (root->val < key) {
        // go to the right subtree
        root->right = deleteNode(root->right, key);
    }
    return root;
}

python

def deleteNode(root: TreeNode, key: int) -> TreeNode:
    if root.val == key:
        # Found it, proceed with deletion
    elif root.val > key:
        # Search in the left subtree
        root.left = deleteNode(root.left, key)
    elif root.val < key:
        # Search in the right subtree
        root.right = deleteNode(root.right, key)
    return root

func deleteNode(root *TreeNode, key int) *TreeNode {
    if root.Val == key {
        // found it, proceed to delete
    } else if root.Val > key {
        // look in the left subtree
        root.Left = deleteNode(root.Left, key)
    } else if root.Val < key {
        // look in the right subtree
        root.Right = deleteNode(root.Right, key)
    }
    return root
}

javascript

var deleteNode = function(root, key) {
    if (root.val === key) {
        // Found it, proceed with deletion
    } else if (root.val > key) {
        // Go to the left subtree to search
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        // Go to the right subtree to search
        root.right = deleteNode(root.right, key);
    }
    return root;
}

After finding the target node, let's say it is node A, how do we delete it? This is the main challenge, because you can't break the properties of the BST. There are three possible cases, shown with pictures.

Case 1: A is a leaf node (both children are null). You can simply delete it.

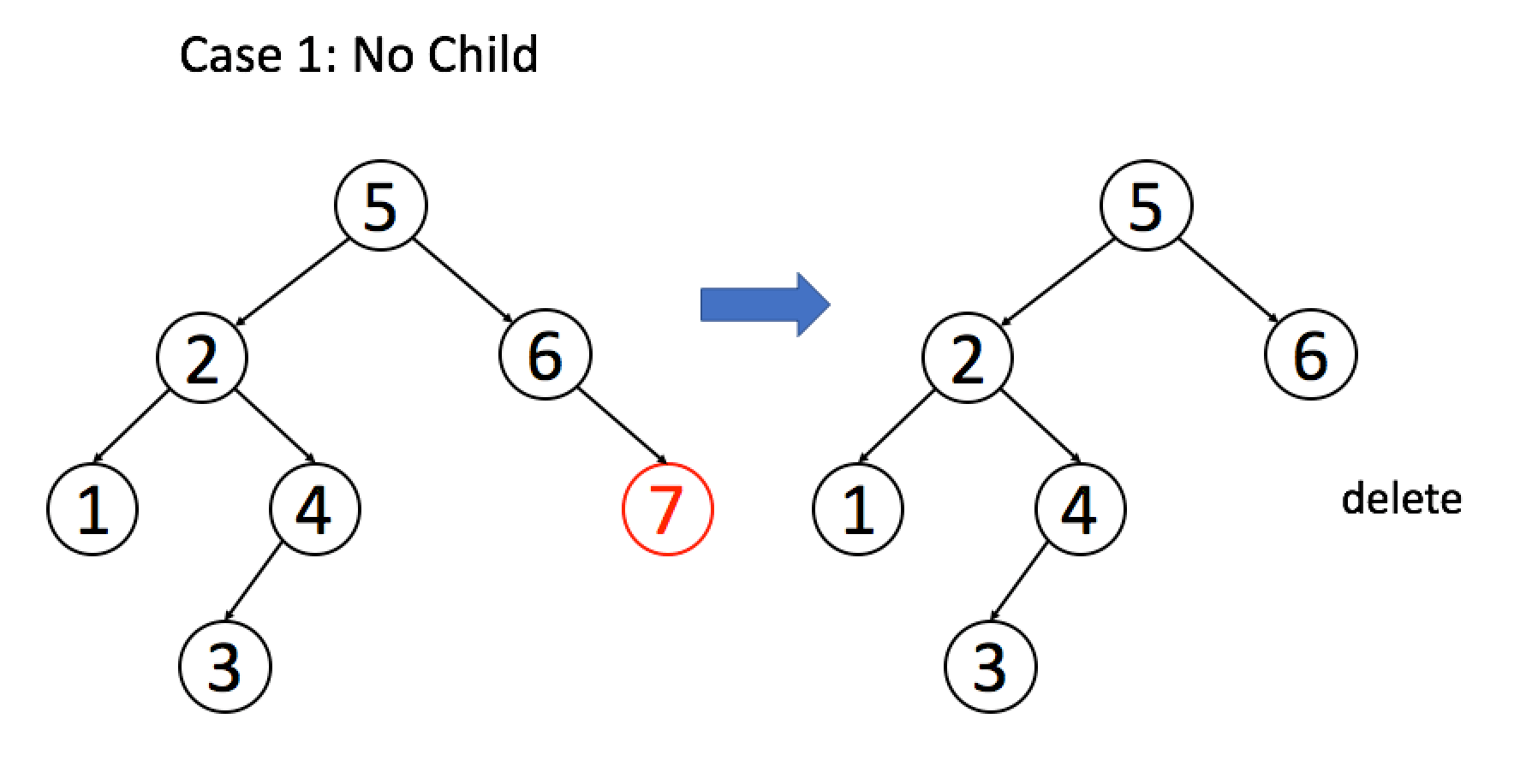
if (root.left == null && root.right == null)
    return null;

Case 2: A has only one non-empty child. Let this child take A's place.

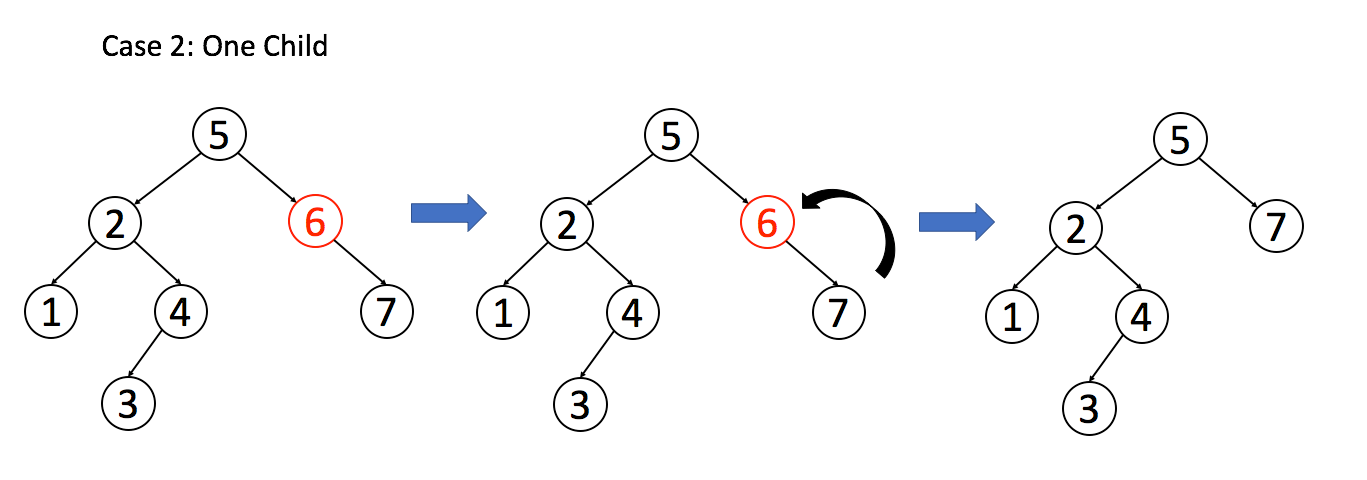
// After excluding case 1
if (root.left == null) return root.right;
if (root.right == null) return root.left;

Case 3: A has two children. This is more complex. To keep the BST property, you must find either the largest node in the left subtree or the smallest node in the right subtree to replace A. We will explain the second way.

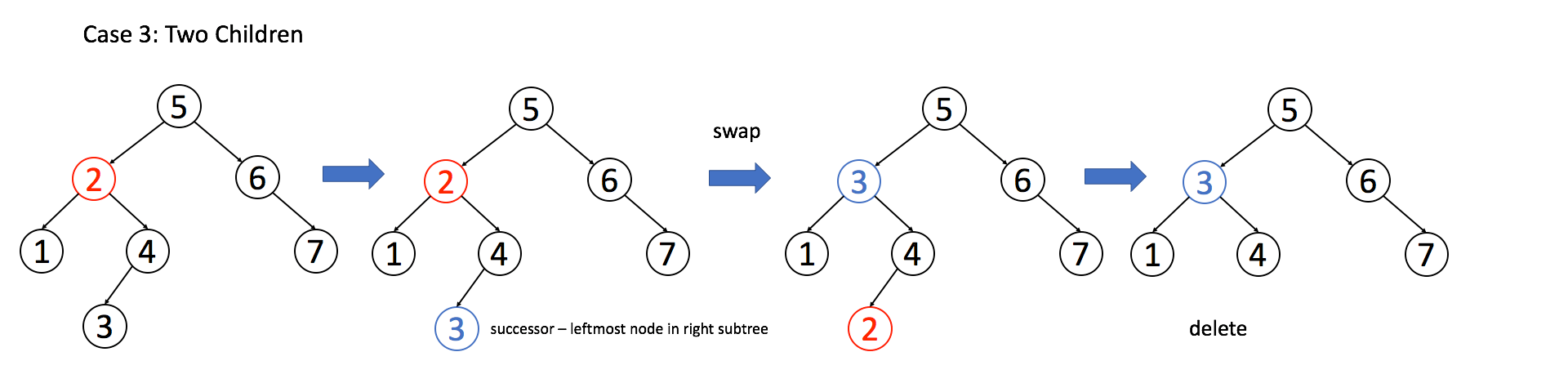
if (root.left != null && root.right != null) {
    // Find the smallest node in the right subtree
    TreeNode minNode = getMin(root.right);
    // Replace root with minNode
    root.val = minNode.val;
    // Delete minNode
    root.right = deleteNode(root.right, minNode.val);
}

After explaining all three cases, fill them into the framework and simplify the code:

java

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val == key) {
            // these two if statements correctly handle cases 1 and 2
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            // handle case 3
            // get the smallest node in the right subtree
            TreeNode minNode = getMin(root.right);
            // delete the smallest node in the right subtree
            root.right = deleteNode(root.right, minNode.val);
            // replace the root node with the smallest node from the right subtree
            minNode.left = root.left;
            minNode.right = root.right;
            root = minNode;
        } else if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        }
        return root;
    }

    TreeNode getMin(TreeNode node) {
        // the leftmost node in a BST is the smallest
        while (node.left != null) node = node.left;
        return node;
    }
}

cpp

class Solution {
public:
    // define: delete the node with value key in the BST
    // rooted at root, return the root after deletion
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return nullptr;
        if (root->val == key) {
            // these two if statements correctly handle cases 1 and 2
            if (root->left == nullptr) return root->right;
            if (root->right == nullptr) return root->left;
            // handle case 3
            // get the smallest node in the right subtree
            TreeNode* minNode = getMin(root->right);
            // delete the smallest node in the right subtree
            root->right = deleteNode(root->right, minNode->val);
            // replace the root node with the smallest node in the right subtree
            minNode->left = root->left;
            minNode->right = root->right;
            root = minNode;
        } else if (root->val > key) {
            root->left = deleteNode(root->left, key);
        } else if (root->val < key) {
            root->right = deleteNode(root->right, key);
        }
        return root;
    }

    TreeNode* getMin(TreeNode* node) {
        // in a BST, the leftmost node is the smallest
        while (node->left != nullptr) node = node->left;
        return node;
    }
};

python

class Solution:
    # define: delete the node with value key in the BST
    # rooted at root, return the root after deletion
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if root == None:
            return None
        if root.val == key:
            # These two if statements correctly handle cases 1 and 2
            if root.left == None:
                return root.right
            if root.right == None:
                return root.left
            # handle case 3
            # get the smallest node in the right subtree
            minNode = self.getMin(root.right)
            # delete the smallest node in the right subtree
            root.right = self.deleteNode(root.right, minNode.val)
            # replace the root node with the smallest node in the right subtree
            minNode.left = root.left
            minNode.right = root.right
            root = minNode
        elif root.val > key:
            root.left = self.deleteNode(root.left, key)
        elif root.val < key:
            root.right = self.deleteNode(root.right, key)
        return root

    def getMin(self, node: TreeNode) -> TreeNode:
        # The leftmost node in a BST is the smallest
        while node.left != None:
            node = node.left
        return node

// define: delete the node with value key in the BST
// rooted at root, return the root after deletion
func deleteNode(root *TreeNode, key int) *TreeNode {
    if root == nil {
        return nil
    }
    if root.Val == key {
        // these two if statements correctly handle cases 1 and 2
        if root.Left == nil {
            return root.Right
        }
        if root.Right == nil {
            return root.Left
        }
        // handle case 3
        // get the smallest node in the right subtree
        minNode := getMin(root.Right)
        // delete the smallest node in the right subtree
        root.Right = deleteNode(root.Right, minNode.Val)
        // replace the root node with the smallest node in the right subtree
        minNode.Left = root.Left
        minNode.Right = root.Right
        root = minNode
    } else if root.Val > key {
        root.Left = deleteNode(root.Left, key)
    } else if root.Val < key {
        root.Right = deleteNode(root.Right, key)
    }
    return root
}

// get the smallest node in the binary search tree
func getMin(node *TreeNode) *TreeNode {
    // the leftmost node in a BST is the smallest
    for node.Left != nil {
        node = node.Left
    }
    return node
}

javascript

// define: delete the node with value key in the BST
// rooted at root, return the root after deletion
var deleteNode = function(root, key) {
    if (root == null) return null;
    if (root.val == key) {
        // These two if-statements handle cases 1 and 2 correctly
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        // handle case 3
        // get the smallest node in the right subtree
        let minNode = getMin(root.right);
        // delete the smallest node in the right subtree
        root.right = deleteNode(root.right, minNode.val);
        // replace the root node with the smallest node in the right subtree
        minNode.left = root.left;
        minNode.right = root.right;
        root = minNode;
    } else if (root.val > key) {
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        root.right = deleteNode(root.right, key);
    }
    return root;
}

// get the smallest node in the BST.
var getMin = function(node) {
    // the leftmost node in the BST is the smallest
    while (node.left != null) node = node.left;
    return node;
}

Algorithm Visualization

Now, the delete operation is finished. Note: In case 3, the code above replaces the root node with minNode by swapping their values, which is a bit simpler:

// Handle case 3
// Get the smallest node in the right subtree
TreeNode minNode = getMin(root.right);
// Delete the smallest node in the right subtree
root.right = deleteNode(root.right, minNode.val);
// Replace root node with the smallest node in the right subtree
minNode.left = root.left;
minNode.right = root.right;
root = minNode;

Some readers may wonder why we need to swap the nodes with pointer operations. Why not just change the val field? It looks easier:

// Handle case 3
// Get the smallest node in the right subtree
TreeNode minNode = getMin(root.right);
// Delete the smallest node in the right subtree
root.right = deleteNode(root.right, minNode.val);
// Replace root node with the smallest node in the right subtree
root.val = minNode.val;

For this algorithm problem, it is fine. But in real applications, we do not swap nodes by just changing the internal value. The data inside a BST node could be very complex, and the BST structure should not care about the actual data. So, we prefer using pointers to swap nodes.

Let's summarize a few key points from this article:

If the current node will affect its children, you can pass information by adding parameters to helper functions.
Master how to insert, delete, search, and update nodes in a BST.
When changing a data structure with recursion, always receive the return value and return the updated node.

That's all for this article. For more classic binary tree problems and recursion practice, see the Recursion Practice for Binary Search Trees in the binary tree chapter.

Related Problems

You can install my Chrome extension then open the link.

LeetCode	Difficulty

Binary Search Tree in Action (Basic Operations)

450. Delete Node in a BST https://leetcode.com/problems/delete-node-in-a-bst

700. Search in a Binary Search Tree https://leetcode.com/problems/search-in-a-binary-search-tree

701. Insert into a Binary Search Tree https://leetcode.com/problems/insert-into-a-binary-search-tree

98. Validate Binary Search Tree https://leetcode.com/problems/validate-binary-search-tree

1. Check if a BST is Valid

Search for an Element in a BST

Insert a Number into a BST

3. Delete a Node in a BST