Binary Search Tree in Action (In-order)

In previous articles, we have walked you through binary trees with Mindset Series, Construction Series, Postorder Series, and Serialization Series.

Today, we start a series on Binary Search Trees (BST, for short) and guide you through solving BST problems step by step.

First, you should be familiar with the characteristics of BST (detailed in the basic knowledge section of Basic Binary Tree Structure):

1. For every node node in a BST, the values of the nodes in the left subtree are smaller than node, and the values of the nodes in the right subtree are larger than node.

2. For every node node in a BST, both its left and right subtrees are also BSTs.

Binary search trees are not complicated, but I believe they are half of the data structure world. Data structures directly based on BST include AVL trees, red-black trees, etc., which have self-balancing properties and can provide logN efficiency for insertions, deletions, and searches. Other structures like B+ trees and segment trees are also designed based on the BST concept.

From the perspective of solving algorithm problems, besides its definition, BST has an important property: the inorder traversal of a BST results in a sorted (ascending) sequence.

This means that if you are given a BST, the following code can print the values of each node in ascending order:

void traverse(TreeNode root) {
    if (root == null) return;
    traverse(root.left);
    // inorder traversal code position
    print(root.val);
    traverse(root.right);
}

void traverse(TreeNode* root) {
    if (root == nullptr) {
       return;
    }
    traverse(root->left);
    // in-order traversal code position
    print(root->val);
    traverse(root->right);
}

def traverse(root):
    if not root:
        return
    traverse(root.left)
    # in-order traversal code position
    print(root.val)
    traverse(root.right)

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.left)
    // inorder traversal code position
    fmt.Println(root.val)
    traverse(root.right)
}

var traverse = function(root) {
  if (root === null) return;
  traverse(root.left);
  // inorder traversal code position
  console.log(root.val);
  traverse(root.right);
};

Based on this property, let's solve two algorithm problems.

Finding the Kth Smallest Element

This is LeetCode problem 230, "Kth Smallest Element in a BST." Let's look at the problem:

230. Kth Smallest Element in a BST | LeetCode |

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

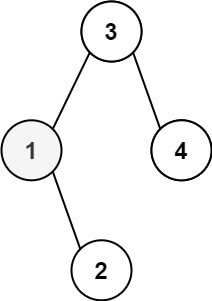
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

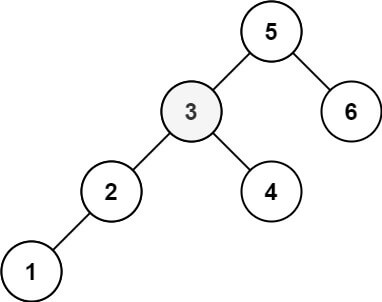
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

• The number of nodes in the tree is n.
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

This requirement is quite common. A straightforward approach is to sort the elements in ascending order and then find the kth element. The inorder traversal of a BST essentially gives us the sorted order, so finding the kth element should be straightforward.

Following this approach, we can directly write the code:

class Solution {
    int kthSmallest(TreeNode root, int k) {
        // Utilize the in-order traversal property of BST
        traverse(root, k);
        return res;
    }

    // Record the result
    int res = 0;
    // Record the rank of the current element
    int rank = 0;
    void traverse(TreeNode root, int k) {
        if (root == null) {
            return;
        }
        traverse(root.left, k);

        // In-order traversal code position
        rank++;
        if (k == rank) {
            // Found the kth smallest element
            res = root.val;
            return;
        }

        traverse(root.right, k);
    }
}

class Solution {
private:
    // record the result
    int res = 0;
    // record the rank of the current element
    int rank = 0;
    void traverse(TreeNode* root, int k) {
        if (root == nullptr) {
            return;
        }
        traverse(root->left, k);

        // inorder traversal code position
        rank++;
        if (k == rank) {
            // found the kth smallest element
            res = root->val;
            return;
        }

        traverse(root->right, k);
    }

public:
    int kthSmallest(TreeNode* root, int k) {
        // utilize the inorder traversal property of BST
        traverse(root, k);
        return res;
    }
};

class Solution:
    def __init__(self):
        # record the result
        self.res = 0
        # record the rank of the current element
        self.rank = 0

    def kthSmallest(self, root: TreeNode, k: int) -> int:
        # utilize the in-order traversal characteristic of BST
        self.traverse(root, k)
        return self.res

    def traverse(self, root, k):
        if not root:
            return
        self.traverse(root.left, k)

        # in-order traversal code position
        self.rank += 1
        if k == self.rank:
            # found the kth smallest element
            self.res = root.val
            return

        self.traverse(root.right, k)

func kthSmallest(root *TreeNode, k int) int {
    // record the result
    res := 0
    // record the rank of the current element
    rank := 0
    var traverse func(root *TreeNode)

    traverse = func(root *TreeNode) {
        if root == nil {
            return
        }
        traverse(root.Left)

        // inorder traversal code position
        rank++
        if k == rank {
            // found the kth smallest element
            res = root.Val
            return
        }

        traverse(root.Right)
    }

    // utilize the inorder traversal property of BST
    traverse(root)
    return res
}

var kthSmallest = function(root, k) {
    // record the result
    let res = 0;
    // record the rank of the current element
    let rank = 0;
    var traverse = function(root) {
        if (root === null) {
            return;
        }
        traverse(root.left);

        // in-order traversal code position
        rank++;
        if (k === rank) {
            // found the kth smallest element
            res = root.val;
            return;
        }

        traverse(root.right);
    }

    // utilize the in-order traversal property of BST
    traverse(root);
    return res;
}

This problem is solved, but it's worth discussing further because this solution is not the most efficient and is specifically tailored for this problem.

We previously mentioned today's issue in the article Efficient Calculation of Median in Data Stream:

Using the method we just discussed, which leverages the property that "in-order traversal of a BST gives a sorted order," finding the k-th smallest element would require an in-order traversal each time, resulting in a worst-case time complexity of $O(N)$, where N is the number of nodes in the BST.

It's important to note that the properties of a BST are quite powerful. For instance, in a self-balancing BST like a Red-Black Tree, operations such as insertion, deletion, search, and update all have a complexity of $O(logN)$. Having a complexity of $O(N)$ to find the k-th smallest element seems inefficient.

Therefore, the best algorithm for finding the k-th smallest element should also have a logarithmic complexity, which depends on how much information each BST node records.

Why are BST operations so efficient? Take searching for an element as an example. A BST can find an element in logarithmic time because of its definition: the left subtree contains smaller values and the right subtree contains larger values. This allows each node to decide whether to search in the left or right subtree by comparing its own value, avoiding a full-tree traversal and achieving logarithmic complexity.

Returning to the problem of finding the k-th smallest element or the element ranked k, achieving logarithmic complexity hinges on each node knowing its own rank.

For instance, if you need to find the element ranked k, and the current node knows its rank is m, you can compare m with k:

1. If m == k, you have found the k-th element, so you return the current node.
2. If k < m, it indicates that the k-th element is in the left subtree, so you search for the k-th element in the left subtree.
3. If k > m, it indicates that the k-th element is in the right subtree, so you search for the k - m - 1-th element in the right subtree.

This approach reduces the time complexity to $O(logN)$.

So, how can each node know its own rank?

This requires maintaining additional information in each tree node. Each node needs to record how many nodes are in the subtree rooted at itself.

In other words, the fields in our TreeNode should be as follows:

class TreeNode {
    int val;
    // total number of nodes in the tree rooted at this node
    int size;
    TreeNode left;
    TreeNode right;
}

class TreeNode {
public:
    int val;
    // total number of nodes in the tree rooted at this node
    int size;
    TreeNode* left;
    TreeNode* right;
};

class TreeNode:
    def __init__(self):
        self.val = None
        # total number of nodes in the tree rooted at this node
        self.size = None
        self.left = None
        self.right = None

type TreeNode struct {
    Val   int
    // total number of nodes in the tree rooted at this node
    Size  int
    Left  *TreeNode
    Right *TreeNode
}

function TreeNode() {
    var val;
    // total number of nodes in the tree rooted at this node
    var size;
    var left;
    var right;
}

With the size field and the property of BST nodes where the left child is smaller and the right child is larger, we can derive the rank of each node node through node.left, achieving the logarithmic-time algorithm we mentioned earlier.

Of course, the size field needs to be correctly maintained when adding or deleting elements. The TreeNode provided by LeetCode does not have a size field, so for this problem, we can only use the in-order traversal property of BST. However, the optimization approach mentioned above is a common operation in BST and is still necessary to understand.

Converting BST to Greater Tree

LeetCode problems 538 and 1038 are the same as this one, so you can solve them together. Here is the problem statement:

538. Convert BST to Greater Tree | LeetCode |

Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

As a reminder, a binary search tree is a tree that satisfies these constraints:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

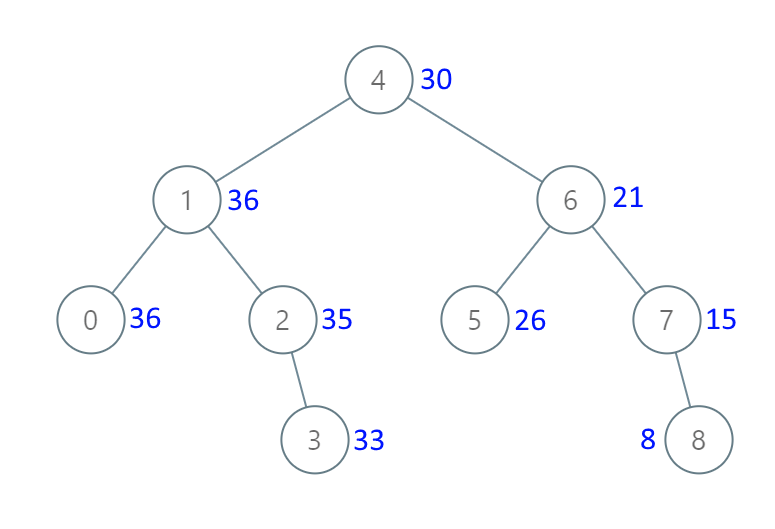
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input: root = [0,null,1]
Output: [1,null,1]

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -104 <= Node.val <= 104
• All the values in the tree are unique.
• root is guaranteed to be a valid binary search tree.

Note: This question is the same as 1038: https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/

The problem should be easy to understand. For example, for the node 5 in the diagram, when converted to a greater tree, the nodes greater than 5 are 6, 7, and 8. Adding 5 itself, the value of this node in the greater tree should be 5+6+7+8=26.

We need to convert the BST into a greater tree. The function signature is as follows:

TreeNode convertBST(TreeNode root)

TreeNode* convertBST(TreeNode* root);

def convertBST(root: TreeNode) -> TreeNode:

func convertBST(root *TreeNode) *TreeNode {}

var convertBST = function(root) {}

Following the general approach for binary trees, we need to think about what each node should do. However, for this problem, it's hard to come up with a clear strategy.

In a Binary Search Tree (BST), each node has smaller values on the left and larger values on the right. This seems like useful information. Since the cumulative sum is the total of all elements greater than or equal to the current value, can't we just calculate the sum of the right subtree for each node?

This won't work. For a given node, it's true that all elements in the right subtree are larger, but the parent node might also be larger. We can't be sure because we don't have a pointer to the parent node. So, the general binary tree approach doesn't apply here.

Since this path is blocked, let's try a different approach, still leveraging the in-order traversal property of BSTs.

Earlier, we mentioned that the in-order traversal of a BST prints node values in ascending order. But what if we want to print the values in descending order?

It's simple. Just change the order of recursion: traverse the right subtree first, then the left subtree:

void traverse(TreeNode root) {
    if (root == null) return;
    // First, recursively traverse the right subtree
    traverse(root.right);
    // Inorder traversal code position
    print(root.val);
    // Then, recursively traverse the left subtree
    traverse(root.left);
}

void traverse(TreeNode* root) {
    if (root == nullptr) return;
    // first recursively traverse the right subtree
    traverse(root->right);
    // in-order traversal code position
    print(root->val);
    // then recursively traverse the left subtree
    traverse(root->left);
}

def traverse(root):
    if root is None:
        return
    # first recursively traverse the right subtree
    traverse(root.right)
    # inorder traversal code position
    print(root.val)
    # then recursively traverse the left subtree
    traverse(root.left)

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // first recursively traverse the right subtree
    traverse(root.Right)
    // inorder traversal code position
    fmt.Println(root.Val)
    // then recursively traverse the left subtree
    traverse(root.Left)
}

var traverse = function(root) {
    if (root == null) return;
    // First recursively traverse the right subtree
    traverse(root.right);
    // In-order traversal code position
    console.log(root.val);
    // Then recursively traverse the left subtree
    traverse(root.left);
}

This code can print the values of BST nodes in descending order. If we maintain an external cumulative variable sum, and then assign sum to each node in the BST, wouldn't that convert the BST into a cumulative tree?

Take a look at the code to understand:

class Solution {
    TreeNode convertBST(TreeNode root) {
        traverse(root);
        return root;
    }

    // record the cumulative sum
    int sum = 0;
    void traverse(TreeNode root) {
        if (root == null) {
            return;
        }
        traverse(root.right);
        // maintain the cumulative sum
        sum += root.val;
        // convert BST to cumulative tree
        root.val = sum;
        traverse(root.left);
    }
}

class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        traverse(root);
        return root;
    }

private:
    // record the cumulative sum
    int sum = 0;
    void traverse(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        traverse(root->right);
        // maintain the cumulative sum
        sum += root->val;
        // convert BST to accumulation tree
        root->val = sum;
        traverse(root->left);
    }
};

class Solution:
        def __init__(self):
            # record the cumulative sum
            self.sum = 0
            
        def convertBST(self, root):
            self.traverse(root)
            return root

        def traverse(self, root):
            if root is None:
                return
            self.traverse(root.right)
            # maintain the cumulative sum
            self.sum += root.val
            # convert BST to cumulative tree
            root.val = self.sum
            self.traverse(root.left)

func convertBST(root *TreeNode) *TreeNode {
    // record the cumulative sum
    sum := 0
    // define a closure for traverse
	traverse := func(root *TreeNode) {}
	traverse = func(root *TreeNode) {
		if root == nil {
			return
		}
		traverse(root.Right)
		// maintain the cumulative sum
		sum += root.Val
		// convert BST to a cumulative tree
		root.Val = sum
		traverse(root.Left)
	}
    traverse(root)
    return root
}

var convertBST = function(root){
    var sum = 0;

    var traverse = function(root) {
        if (root == null) {
            return;
        }
        traverse(root.right);
        // maintain the cumulative sum
        sum += root.val;
        // convert BST to cumulative tree
        root.val = sum;
        traverse(root.left);
    } 

    traverse(root);
    return root;
}

This problem is solved by leveraging the in-order traversal property of BST (Binary Search Tree). We simply modified the recursive order to traverse the BST in descending order, aligning with the requirements of the cumulative tree problem.

To summarize briefly, BST-related problems either utilize the BST property of smaller values on the left and larger on the right to enhance algorithm efficiency, or use the in-order traversal property to meet specific problem requirements. That's pretty much it.

This article ends here. For more classic binary tree exercises and recursive thinking training, please refer to the Exercise Section in the binary tree chapter.