How to Determine a Bipartite Graph
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 785. Is Graph Bipartite? | 🟠 |
| 886. Possible Bipartition | 🟠 |
Prerequisites
Before reading this article, you should learn:
Today, let's talk about a classic graph algorithm: checking if a graph is bipartite.
Introduction to Bipartite Graphs
Let's look at the definition of a bipartite graph:
A bipartite graph is a graph whose vertices can be divided into two groups, and every edge connects a vertex from one group to a vertex from the other group. No two vertices in the same group are connected by an edge.
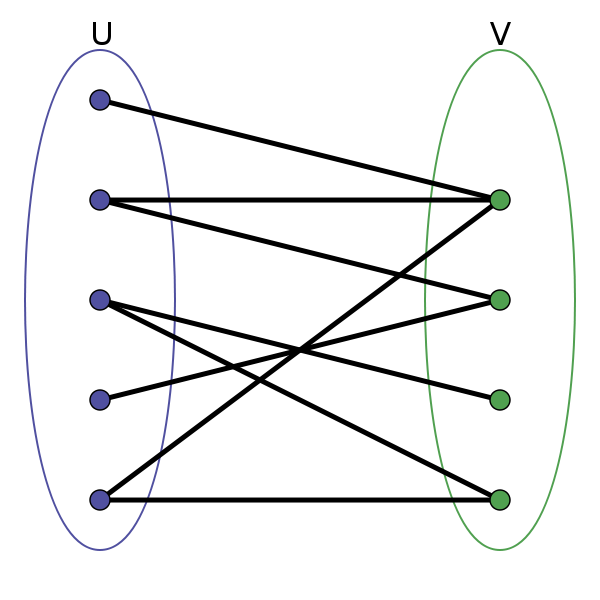
Graph theory often has definitions that are hard to understand. Let's not worry about the strict definition for now. Let’s play a game:
Given a "graph", can you color all the nodes using two colors, so that no two connected nodes have the same color?
This is called the "two-color problem" for graphs. In fact, solving this problem is the same as checking if a graph is bipartite. If you can color the graph this way, then the graph is bipartite; if not, then it is not:
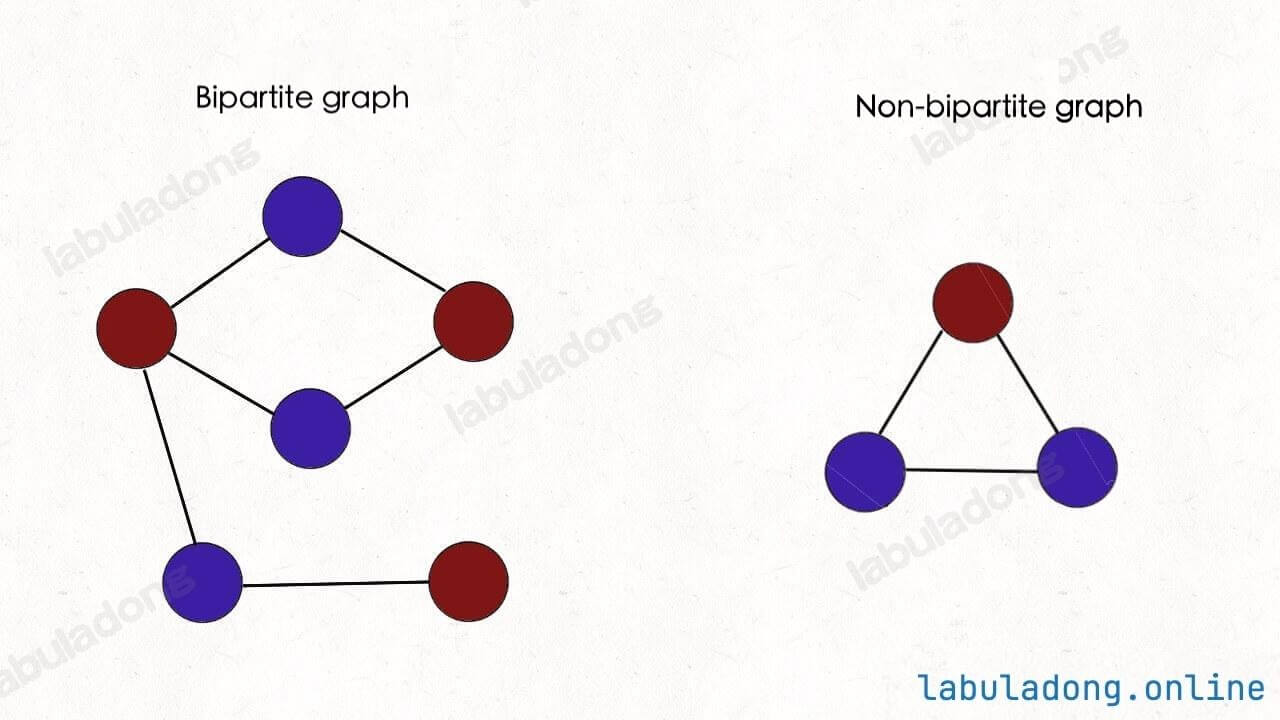
Before we talk about the algorithm to check bipartite graphs, let's discuss why computer scientists care about the two-color problem.
First, bipartite graphs are a special type of graph. Many advanced algorithms, like the maximum flow algorithm, use bipartite graphs. If you are interested, you can search for more information, but it’s not required.
From a simple and practical point of view, bipartite graphs can be used to store data more efficiently in some situations.
For example, suppose we want to store the relationship between movies and actors: a movie usually has several actors, and an actor can act in several movies. What data structure would you use to store this relationship?
Since we want to store mappings, the simplest way is to use a hash table. We can use a HashMap<String, List<String>> to map a movie to its list of actors. If we know a movie’s name, we can quickly find all its actors.
But what if we have an actor’s name and want to find all the movies this actor has appeared in? We would need to create another hash table, mapping actors to their movies.
So, if we use hash tables, we need two: one to map actors to movies, and one to map movies to actors. But if we use a "graph" structure, we can simply connect movies and actors together, which naturally forms a bipartite graph:
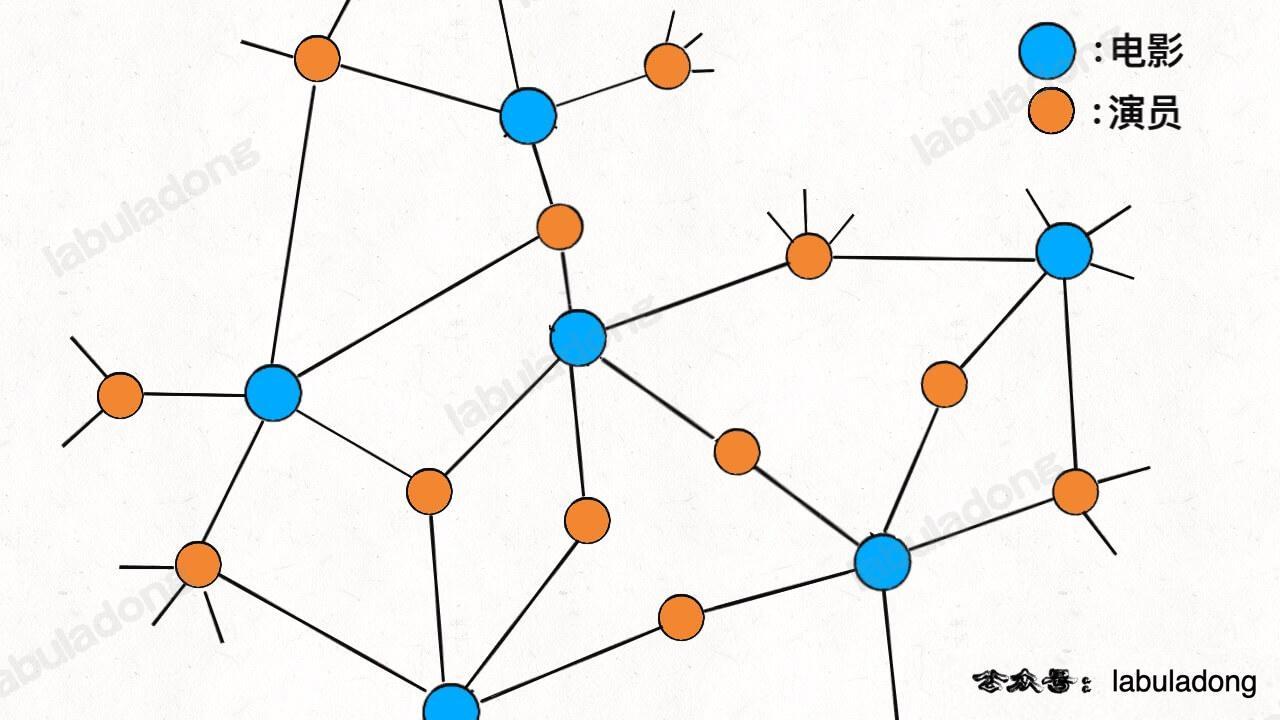
For each movie node, its neighbors are the actors in the movie. For each actor node, its neighbors are the movies they acted in. Compared with hash tables, this is more direct and uses less storage.
In fact, many real-world relationships can be represented as bipartite graphs. In some cases, graphs can also be used as data structures for storing key-value pairs (symbol tables).
Now, let’s get to the main topic: how to check if a graph is bipartite.
How to Check If a Graph Is Bipartite
The algorithm is simple. It is just solving the "two-color problem" with code.
In short, we traverse the graph, coloring nodes as we go. We try to use only two colors so that no connected nodes have the same color.
Since we need to traverse the graph, and we don’t need to find the shortest path, both DFS and BFS work. DFS is more common, so let's see how to use DFS to check if a graph is bipartite.
First, based on graph traversal, let’s write the DFS framework for traversing a graph:
// traverse all nodes of the graph
void traverse(Graph graph, int s, boolean[] visited) {
// base case
if (s < 0 || s >= graph.size()) {
return;
}
if (visited[s]) {
// prevent infinite loop
return;
}
// pre-order position
visited[s] = true;
System.out.println("visit " + s);
for (Edge e : graph.neighbors(s)) {
traverse(graph, e.to, visited);
}
// post-order position
}// traverse all nodes of the graph
void traverse(const Graph& graph, int s, std::vector<bool>& visited) {
// base case
if (s < 0 || s >= graph.size()) {
return;
}
if (visited[s]) {
// prevent infinite loop
return;
}
// pre-order position
visited[s] = true;
std::cout << "visit " << s << std::endl;
for (const Graph::Edge& e : graph.neighbors(s)) {
traverse(graph, e.to, visited);
}
// post-order position
}# traverse all nodes of the graph
def traverse(graph, s, visited):
# base case
if s < 0 or s >= len(graph):
return
if visited[s]:
# prevent infinite loop
return
# pre-order position
visited[s] = True
print("visit", s)
for e in graph.neighbors(s):
traverse(graph, e.to, visited)
# post-order position// traverse all nodes of the graph
func traverse(graph Graph, s int, visited []bool) {
// base case
if s < 0 || s >= len(graph) {
return
}
if visited[s] {
// prevent infinite loop
return
}
// pre-order position
visited[s] = true
fmt.Println("visit", s)
for _, e := range graph.neighbors(s) {
traverse(graph, e.to, visited)
}
// post-order position
}// traverse all nodes of the graph
var traverse = function(graph, s, visited) {
// base case
if (s < 0 || s >= graph.size()) {
return;
}
if (visited[s]) {
// prevent infinite loop
return;
}
// pre-order position
visited[s] = true;
console.log("visit " + s);
for (var e of graph.neighbors(s)) {
traverse(graph, e.to, visited);
}
// post-order position
};Since there might be cycles in the graph, a visited array is used to prevent revisiting nodes.
You can see that I like to place all the return statements at the beginning of the function because return statements are usually the base cases. Grouping them together makes the algorithm structure clearer.
In fact, if you prefer, you can place the if conditions elsewhere. For example, the graph traversal framework can be slightly adjusted:
// graph traversal framework
boolean[] visited;
void traverse(Graph graph, int v) {
// pre-order traversal position, mark node v as visited
visited[v] = true;
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// only traverse unvisited neighboring nodes
traverse(graph, neighbor);
}
}
}// graph traversal framework
std::vector<bool> visited;
void traverse(Graph &graph, int v) {
// pre-order traversal position, mark node v as visited
visited[v] = true;
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// only traverse unmarked neighboring nodes
traverse(graph, neighbor);
}
}
}# graph traversal framework
visited = []
def traverse(graph: Graph, v: int):
# pre-order traversal position, mark node v as visited
visited[v] = True
for neighbor in graph.neighbors(v):
if not visited[neighbor]:
# only traverse unmarked neighboring nodes
traverse(graph, neighbor)// define a function to traverse the graph
var visited []bool
func traverse(graph *Graph, v int) {
// pre-order traversal position, mark node v as visited
visited[v] = true
for _, neighbor := range graph.neighbors(v) {
if !visited[neighbor] {
// only traverse the unvisited neighboring nodes
traverse(graph, neighbor)
}
}
}// Graph traversal framework
var visited = [];
var traverse = function(graph, v) {
// Pre-order traversal position, mark node v as visited
visited[v] = true;
var neighbors = graph.neighbors(v);
for (var i = 0; i < neighbors.length; i++) {
if (!visited[neighbors[i]]) {
// Only traverse unmarked neighboring nodes
traverse(graph, neighbors[i]);
}
}
};This approach places the check for visited before the recursive call. The only difference from the previous approach is that you need to ensure visited[v] == false when calling traverse(v).
Why mention this specific approach? Because we use this method in the algorithm to determine bipartite graphs.
To recall how to determine a bipartite graph, the traverse function is used to traverse the nodes and color them, attempting to make the colors of every pair of adjacent nodes different.
Therefore, the code logic to determine a bipartite graph can be written like this:
// graph traversal framework
void traverse(Graph graph, boolean[] visited, int v) {
visited[v] = true;
// traverse all adjacent nodes of node v
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// the adjacent node neighbor has not been visited
// then we should color node neighbor with a different color from node v
traverse(graph, visited, neighbor);
} else {
// the adjacent node neighbor has already been visited
// then we should compare the colors of node neighbor and node v
// if they are the same, then this graph is not a bipartite graph
}
}
}// graph traversal framework
void traverse(Graph &graph, vector<bool> &visited, int v) {
visited[v] = true;
// traverse all adjacent nodes of node v
for(auto neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// adjacent node neighbor has not been visited
// then node neighbor should be colored differently from node v
traverse(graph, visited, neighbor);
} else {
// adjacent node neighbor has already been visited
// then the colors of node neighbor and node v should be compared
// if they are the same, the graph is not bipartite
}
}
}# graph traversal framework
def traverse(graph, visited, v):
visited[v] = True
# traverse all adjacent nodes of node v, called neighbor
for neighbor in graph.neighbors(v):
if not visited[neighbor]:
# adjacent node neighbor has not been visited
# then node neighbor should be colored differently from node v
traverse(graph, visited, neighbor)
else:
# adjacent node neighbor has already been visited
# then we should compare the colors of node neighbor and node v
# if they are the same, then this graph is not a bipartite graph
pass// graph traversal framework
func traverse(graph Graph, visited []bool, v int) {
visited[v] = true
// traverse all adjacent nodes of node v
for _, neighbor := range graph.neighbors(v) {
if !visited[neighbor] {
// adjacent node neighbor has not been visited
// then node neighbor should be colored with a different color from node v
traverse(graph, visited, neighbor)
} else {
// adjacent node neighbor has already been visited
// then we should compare the colors of node neighbor and node v
// if they are the same, then this graph is not a bipartite graph
}
}
}// graph traversal framework
var traverse = function(graph, visited, v) {
visited[v] = true;
// traverse all adjacent nodes of node v, neighbor
for (var neighbor of graph.neighbors(v)) {
if (!visited[neighbor]) {
// adjacent node neighbor has not been visited
// then we should color node neighbor with a different color from node v
traverse(graph, visited, neighbor);
} else {
// adjacent node neighbor has already been visited
// then we should compare the colors of node neighbor and node v
// if they are the same, then this graph is not a bipartite graph
}
}
}If you can understand the above code, you can write the specific code for determining a bipartite graph. Next, let's practice with two specific algorithm problems.
Problem Practice
LeetCode Problem 785 "Is Graph Bipartite?" is the original problem. You are given an input of an adjacency list representing an undirected graph. Your task is to determine if this graph is a bipartite graph.
The function signature is as follows:
boolean isBipartite(int[][] graph);bool isBipartite(vector<vector<int>>& graph);def isBipartite(graph: List[List[int]]) -> bool:func isBipartite(graph [][]int) boolvar isBipartite = function(graph) {
};For example, in the given input adjacency list graph = [[1,2,3],[0,2],[0,1,3],[0,2]], which represents the following graph:
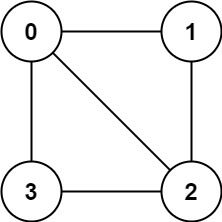
It is clear that the nodes cannot be colored such that every two adjacent nodes have different colors, so the algorithm returns false.
However, if the input is graph = [[1,3],[0,2],[1,3],[0,2]], representing the following graph:
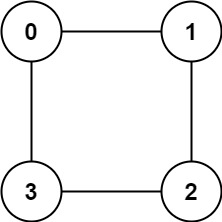
By coloring nodes {0, 2} with one color and nodes {1, 3} with another color, the "two-color problem" can be solved, making it a bipartite graph, so the algorithm returns true.
In conjunction with the previous code framework, we can use an additional color array to record the color of each node, thus writing the solution code:
class Solution {
// record whether the graph is a bipartite graph
private boolean ok = true;
// record the color of the nodes in the graph, false and true represent two different colors
private boolean[] color;
// record whether the nodes in the graph have been visited
private boolean[] visited;
// main function, input adjacency list, determine if it is a bipartite graph
public boolean isBipartite(int[][] graph) {
int n = graph.length;
color = new boolean[n];
visited = new boolean[n];
// because the graph may not be connected, there may be multiple subgraphs
// so we need to traverse each node as a starting point
// if any subgraph is not a bipartite graph, the entire graph is not a bipartite graph
for (int v = 0; v < n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
// dfs traversal framework
private void traverse(int[][] graph, int v) {
// if it has been determined that it is not a bipartite graph,
// there is no need to waste time on recursive traversal
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
// the adjacent node w has not been visited
// so node w should be colored with a different color from node v
color[w] = !color[v];
// continue to traverse w
traverse(graph, w);
} else {
// the adjacent node w has already been visited
// determine if it is a bipartite graph based on the colors of v and w
if (color[w] == color[v]) {
// if the same, the graph is not a bipartite graph
ok = false;
}
}
}
}
}class Solution {
// record whether the graph is a bipartite graph
private:
bool ok = true;
// record the color of the nodes in the graph, false
// and true represent two different colors
vector<bool> color;
// record whether the nodes in the graph have been visited
vector<bool> visited;
// dfs traversal framework
void traverse(const vector<vector<int>>& graph, int v) {
// if it has been determined that it is not a bipartite graph,
// there is no need to waste time on recursive traversal
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
// the adjacent node w has not been visited
// so node w should be colored with a different color from node v
color[w] = !color[v];
// continue to traverse w
traverse(graph, w);
} else {
// the adjacent node w has already been visited
// determine if it is a bipartite graph based on the colors of v and w
if (color[w] == color[v]) {
// if the same, the graph is not a bipartite graph
ok = false;
}
}
}
}
public:
// main function, input adjacency list, determine if it is a bipartite graph
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
color = vector<bool>(n);
visited = vector<bool>(n);
// because the graph may not be connected, there may be multiple subgraphs
// so we need to traverse each node as a starting point
// if any subgraph is not a bipartite graph, the
// entire graph is not a bipartite graph
for (int v = 0; v < n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
};class Solution:
# record whether the graph is a bipartite graph
# record the color of the nodes in the graph, false and true represent two different colors
# record whether the nodes in the graph have been visited
def __init__(self):
self.ok = True
self.color = None
self.visited = None
# main function, input adjacency list, determine if it is a bipartite graph
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
self.color = [False] * n
self.visited = [False] * n
# because the graph may not be connected, there may be multiple subgraphs
# so we need to traverse each node as a starting point
# if any subgraph is not a bipartite graph, the entire graph is not a bipartite graph
for v in range(n):
if not self.visited[v]:
self.traverse(graph, v)
return self.ok
# dfs traversal framework
def traverse(self, graph: List[List[int]], v: int) -> None:
# if it has been determined that it is not a bipartite graph,
# there is no need to waste time on recursive traversal
if not self.ok:
return
self.visited[v] = True
for w in graph[v]:
if not self.visited[w]:
# the adjacent node w has not been visited
# so node w should be colored with a different color from node v
self.color[w] = not self.color[v]
# continue to traverse w
self.traverse(graph, w)
else:
# the adjacent node w has already been visited
# determine if it is a bipartite graph based on the colors of v and w
if self.color[w] == self.color[v]:
# if the same, the graph is not a bipartite graph
self.ok = False// main function, input adjacency list, determine if it is a bipartite graph
func isBipartite(graph [][]int) bool {
n := len(graph)
// record the color of the nodes in the graph, false and true represent two different colors
color := make([]bool, n)
// record whether the nodes in the graph have been visited
visited := make([]bool, n)
// record whether the graph is a bipartite graph
ok := true
// because the graph may not be connected, there may be multiple subgraphs
// so we need to traverse each node as a starting point
// if any subgraph is not a bipartite graph, the entire graph is not a bipartite graph
for v := 0; v < n; v++ {
if !visited[v] {
traverse(graph, v, color, visited, &ok)
}
}
return ok
}
// dfs traversal framework
func traverse(graph [][]int, v int, color []bool, visited []bool, ok *bool) {
// if it has been determined that it is not a bipartite graph,
// there is no need to waste time on recursive traversal
if !*ok {
return
}
visited[v] = true
for _, w := range graph[v] {
if !visited[w] {
// the adjacent node w has not been visited
// so node w should be colored with a different color from node v
color[w] = !color[v]
// continue to traverse w
traverse(graph, w, color, visited, ok)
} else {
// the adjacent node w has already been visited
// determine if it is a bipartite graph based on the colors of v and w
if color[w] == color[v] {
// if the same, the graph is not a bipartite graph
*ok = false
}
}
}
}var isBipartite = function(graph) {
// record whether the graph is a bipartite graph
let ok = true;
// record the color of the nodes in the graph, false and true represent two different colors
let color = new Array(graph.length).fill(false);
// record whether the nodes in the graph have been visited
let visited = new Array(graph.length).fill(false);
// dfs traversal framework
var traverse = function(graph, v) {
// if it has been determined that it is not a bipartite graph,
// there is no need to waste time on recursive traversal
if (!ok) return;
visited[v] = true;
for (let w of graph[v]) {
if (!visited[w]) {
// the adjacent node w has not been visited
// so node w should be colored with a different color from node v
color[w] = !color[v];
// continue to traverse w
traverse(graph, w);
} else {
// the adjacent node w has already been visited
// determine if it is a bipartite graph based on the colors of v and w
if (color[w] === color[v]) {
// if the same, the graph is not a bipartite graph
ok = false;
}
}
}
};
// main function, input adjacency list, determine if it is a bipartite graph
let n = graph.length;
// because the graph may not be connected, there may be multiple subgraphs
// so we need to traverse each node as a starting point
// if any subgraph is not a bipartite graph, the entire graph is not a bipartite graph
for (let v = 0; v < n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
};You can click the line visited[v] = true; multiple times to observe the node coloring process.
Algorithm Visualization
Next, let's look at the logic of the BFS algorithm:
class Solution {
// record whether the graph is bipartite
private boolean ok = true;
// record the color of each node in the graph; false and true represent two different colors
private boolean[] color;
// record whether each node in the graph has been visited
private boolean[] visited;
public boolean isBipartite(int[][] graph) {
int n = graph.length;
color = new boolean[n];
visited = new boolean[n];
for (int v = 0; v < n; v++) {
if (!visited[v]) {
// use the BFS function instead
bfs(graph, v);
}
}
return ok;
}
// perform BFS traversal starting from the start node
private void bfs(int[][] graph, int start) {
Queue<Integer> q = new LinkedList<>();
visited[start] = true;
q.offer(start);
while (!q.isEmpty() && ok) {
int v = q.poll();
// spread from node v to all adjacent nodes
for (int w : graph[v]) {
if (!visited[w]) {
// adjacent node w has not been visited
// therefore, node w should be colored differently from node v
color[w] = !color[v];
// mark node w and add it to the queue
visited[w] = true;
q.offer(w);
} else {
// adjacent node w has already been visited
// determine if the graph is bipartite based on the colors of v and w
if (color[w] == color[v]) {
// if they are the same, then the graph is not bipartite
ok = false;
return;
}
}
}
}
}
}class Solution {
public:
// record whether the graph is bipartite
bool ok = true;
// record the color of each node in the graph, false and true represent two different colors
vector<bool> color;
// record whether each node in the graph has been visited
vector<bool> visited;
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
color.resize(n);
visited.resize(n);
for (int v = 0; v < n; v++) {
if (!visited[v]) {
// use the BFS function instead
bfs(graph, v);
}
}
return ok;
}
// perform BFS traversal starting from the start node
void bfs(vector<vector<int>>& graph, int start) {
queue<int> q;
visited[start] = true;
q.push(start);
while (!q.empty() && ok) {
int v = q.front();
q.pop();
// spread from node v to all adjacent nodes
for (int w : graph[v]) {
if (!visited[w]) {
// adjacent node w has not been visited
// so node w should be colored differently from node v
color[w] = !color[v];
// mark node w and put it in the queue
visited[w] = true;
q.push(w);
} else {
// adjacent node w has already been visited
// determine whether the graph is bipartite based on the colors of v and w
if (color[w] == color[v]) {
// if the same, then the graph is not bipartite
ok = false;
return;
}
}
}
}
}
};from collections import deque
class Solution:
def __init__(self):
# record whether the graph is a bipartite graph
self.ok = True
# record the color of the nodes in the graph, False
# and True represent two different colors
self.color = []
# record whether the nodes in the graph have been visited
self.visited = []
def isBipartite(self, graph):
n = len(graph)
self.color = [False]*n
self.visited = [False]*n
for v in range(n):
if not self.visited[v]:
# change to use BFS function
self.bfs(graph, v)
return self.ok
# perform BFS traversal starting from the start node
def bfs(self, graph, start):
q = deque([start])
self.visited[start] = True
while q and self.ok:
v = q.popleft()
# spread from node v to all adjacent nodes
for w in graph[v]:
if not self.visited[w]:
# adjacent node w has not been visited
# then node w should be colored differently from node v
self.color[w] = not self.color[v]
# mark node w and put it in the queue
self.visited[w] = True
q.append(w)
else:
# adjacent node w has already been visited
# determine if it's a bipartite graph based on the colors of v and w
if self.color[w] == self.color[v]:
# if the same, then the graph is not a bipartite graph
self.ok = False
return// Determine if the graph is bipartite
func isBipartite(graph [][]int) bool {
// Record if the graph satisfies bipartite properties
ok := true
n := len(graph)
// Record the color of each node in the graph, false and true represent two different colors
color := make([]bool, n)
// Record if each node in the graph has been visited
visited := make([]bool, n)
// Start BFS traversal from the start node
var bfs func(start int)
bfs = func(start int) {
q := []int{}
visited[start] = true
q = append(q, start)
for len(q) > 0 && ok {
v := q[0]
q = q[1:]
// Spread from node v to all adjacent nodes
for _, w := range graph[v] {
if !visited[w] {
// Adjacent node w has not been visited
// Node w should be colored differently from node v
color[w] = !color[v]
// Mark node w and add it to the queue
visited[w] = true
q = append(q, w)
} else {
// Adjacent node w has already been visited
// Determine if it is a bipartite graph based on the colors of v and w
if color[w] == color[v] {
// If the colors are the same, the graph is not bipartite
ok = false
return
}
}
}
}
}
for v := 0; v < n && ok; v++ {
if !visited[v] {
// Use the BFS function
bfs(v)
}
}
return ok
}var isBipartite = function(graph) {
// record whether the graph is bipartite
let ok = true;
// record the colors of nodes in the graph, false and true represent two different colors
let color = Array(graph.length);
// record whether nodes in the graph have been visited
let visited = Array(graph.length);
// start BFS traversal from the start node
var bfs = function(start) {
let q = [];
visited[start] = true;
q.push(start);
while (q.length && ok) {
let v = q.shift();
// spread from node v to all adjacent nodes
for (let w of graph[v]) {
if (!visited[w]) {
// adjacent node w has not been visited
// node w should be colored with a different color than node v
color[w] = !color[v];
// mark node w and put it into the queue
visited[w] = true;
q.push(w);
} else {
// adjacent node w has already been visited
// determine whether it is a bipartite graph based on the colors of v and w
if (color[w] == color[v]) {
// if they are the same, then the graph is not bipartite
ok = false;
return;
}
}
}
}
};
let n = graph.length;
// because the graph may not be connected, there may be multiple subgraphs
// therefore, each node should be used as a starting point for traversal
// if any subgraph is found to be not bipartite,
// the entire graph is not considered bipartite
for (let v = 0; v < n; v++) {
if (!visited[v]) {
// switch to using the BFS function
bfs(v);
}
}
return ok;
};The core logic is identical to the previously implemented traverse function (DFS algorithm), which also judges based on the colors of adjacent nodes v and w. For a discussion on the BFS algorithm framework, refer to the previous articles BFS Algorithm Framework and Dijkstra Algorithm Template, which will not be elaborated here.
Finally, let's look at LeetCode Problem 886 "Possible Bipartition":
886. Possible Bipartition | LeetCode | 🟠
We want to split a group of n people (labeled from 1 to n) into two groups of any size. Each person may dislike some other people, and they should not go into the same group.
Given the integer n and the array dislikes where dislikes[i] = [ai, bi] indicates that the person labeled ai does not like the person labeled bi, return true if it is possible to split everyone into two groups in this way.
Example 1:
Input: n = 4, dislikes = [[1,2],[1,3],[2,4]] Output: true Explanation: The first group has [1,4], and the second group has [2,3].
Example 2:
Input: n = 3, dislikes = [[1,2],[1,3],[2,3]] Output: false Explanation: We need at least 3 groups to divide them. We cannot put them in two groups.
Constraints:
1 <= n <= 20000 <= dislikes.length <= 104dislikes[i].length == 21 <= ai < bi <= n- All the pairs of
dislikesare unique.
// The function signature is as follows
boolean possibleBipartition(int n, int[][] dislikes);// The function signature is as follows
bool possibleBipartition(int n, vector<vector<int>>& dislikes);# The function signature is as follows
def possibleBipartition(n: int, dislikes: List[List[int]]):// The function signature is as follows
func possibleBipartition(n int, dislikes [][]int) bool// The function signature is as follows
var possibleBipartition = function(n, dislikes) {}This problem essentially tests the determination of a bipartite graph:
If you consider each person as a node in the graph and the dislike relationship as an edge, the dislikes array forms a graph;
Since the problem states that people who dislike each other cannot be in the same group, it means that all adjacent nodes in the graph must be in two different groups.
This brings us back to the "two-color problem." If it is possible to color all nodes with two colors where adjacent nodes have different colors, then you can divide these nodes into two groups based on their colors.
Therefore, the solution emerges. We construct a graph from the dislikes array and then execute the bipartite graph determination algorithm:
class Solution {
private boolean ok = true;
private boolean[] color;
private boolean[] visited;
public boolean possibleBipartition(int n, int[][] dislikes) {
// graph node numbering starts from 1
color = new boolean[n + 1];
visited = new boolean[n + 1];
// convert the graph into an adjacency list
List<Integer>[] graph = buildGraph(n, dislikes);
for (int v = 1; v <= n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
// build graph function
private List<Integer>[] buildGraph(int n, int[][] dislikes) {
// graph node numbering is 1...n
List<Integer>[] graph = new LinkedList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : dislikes) {
int v = edge[1];
int w = edge[0];
// "Undirected graph" is equivalent to "bidirectional graph"
// v -> w
graph[v].add(w);
// w -> v
graph[w].add(v);
}
return graph;
}
// this traverse function is exactly the same as the one used to determine a bipartite graph
private void traverse(List<Integer>[] graph, int v) {
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
color[w] = !color[v];
traverse(graph, w);
} else {
if (color[w] == color[v]) {
ok = false;
}
}
}
}
}class Solution {
private:
bool ok = true;
vector<bool> color;
vector<bool> visited;
public:
bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
// graph node numbering starts from 1
color.resize(n + 1);
visited.resize(n + 1);
// convert the graph into an adjacency list
vector<vector<int>> graph = buildGraph(n, dislikes);
for (int v = 1; v <= n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
private:
// build graph function
vector<vector<int>> buildGraph(int n, vector<vector<int>>& dislikes) {
// graph node numbering is 1...n
vector<vector<int>> graph(n + 1);
for (const auto& edge : dislikes) {
int v = edge[1];
int w = edge[0];
// "Undirected graph" is equivalent to "bidirectional graph"
// v -> w
graph[v].push_back(w);
// w -> v
graph[w].push_back(v);
}
return graph;
}
// this traverse function is exactly the same as the one used to determine a bipartite graph
void traverse(const vector<vector<int>>& graph, int v) {
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
color[w] = !color[v];
traverse(graph, w);
} else {
if (color[w] == color[v]) {
ok = false;
}
}
}
}
};class Solution:
def __init__(self):
self.ok = True
self.color = None
self.visited = None
def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:
# graph node numbering starts from 1
self.color = [False] * (n + 1)
self.visited = [False] * (n + 1)
# convert the graph into an adjacency list
graph = self.buildGraph(n, dislikes)
for v in range(1, n + 1):
if not self.visited[v]:
self.traverse(graph, v)
return self.ok
# build graph function
def buildGraph(self, n: int, dislikes: List[List[int]]) -> List[List[int]]:
# graph node numbering is 1...n
graph = [[] for _ in range(n + 1)]
for edge in dislikes:
v = edge[1]
w = edge[0]
# "Undirected graph" is equivalent to "bidirectional graph"
# v -> w
graph[v].append(w)
# w -> v
graph[w].append(v)
return graph
# this traverse function is exactly the same as the one used to determine a bipartite graph
def traverse(self, graph: List[List[int]], v: int):
if not self.ok:
return
self.visited[v] = True
for w in graph[v]:
if not self.visited[w]:
self.color[w] = not self.color[v]
self.traverse(graph, w)
else:
if self.color[w] == self.color[v]:
self.ok = False// possibleBipartition determines if it's possible to bipartition the graph
func possibleBipartition(n int, dislikes [][]int) bool {
// graph node numbering starts from 1
// convert the graph into an adjacency list
graph := buildGraph(n, dislikes)
color := make([]bool, n+1)
visited := make([]bool, n+1)
// Try to color the graph
for v := 1; v <= n; v++ {
if !visited[v] {
if !traverse(graph, v, color, visited) {
return false
}
}
}
return true
}
// buildGraph converts the edge list to an adjacency list representation of the graph
// build graph function
func buildGraph(n int, dislikes [][]int) [][]int {
// graph node numbering is 1...n
graph := make([][]int, n+1)
for i := 1; i <= n; i++ {
graph[i] = make([]int, 0)
}
for _, edge := range dislikes {
v, w := edge[1], edge[0]
// "Undirected graph" is equivalent to "bidirectional graph"
graph[v] = append(graph[v], w)
graph[w] = append(graph[w], v)
}
return graph
}
// traverse performs DFS on the graph to check if it can be colored properly
// this traverse function is exactly the same as the one used to determine a bipartite graph
func traverse(graph [][]int, v int, color []bool, visited []bool) bool {
visited[v] = true
for _, w := range graph[v] {
if !visited[w] {
color[w] = !color[v]
if !traverse(graph, w, color, visited) {
return false
}
} else if color[w] == color[v] {
return false
}
}
return true
}var possibleBipartition = function(n, dislikes) {
let ok = true;
let color = new Array(n + 1).fill(false);
let visited = new Array(n + 1).fill(false);
// graph node numbering starts from 1
// convert the graph into an adjacency list
let graph = buildGraph(n, dislikes);
for (let v = 1; v <= n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
// build graph function
function buildGraph(n, dislikes) {
// graph node numbering is 1...n
let graph = new Array(n + 1).fill(0).map(() => []);
for (let i = 1; i <= n; i++) {
graph[i] = [];
}
for (let edge of dislikes) {
let v = edge[1];
let w = edge[0];
// "Undirected graph" is equivalent to "bidirectional graph"
// v -> w
graph[v].push(w);
// w -> v
graph[w].push(v);
}
return graph;
}
// this traverse function is exactly the same as the one used to determine a bipartite graph
function traverse(graph, v) {
if (!ok) return;
visited[v] = true;
for (let w of graph[v]) {
if (!visited[w]) {
color[w] = !color[v];
traverse(graph, w);
} else {
if (color[w] == color[v]) {
ok = false;
}
}
}
}
};Algorithm Visualization
At this point, this problem is also solved using the DFS algorithm. If you want to use the BFS algorithm, it is similar to the previous solution. During the spread, try coloring the adjacent elements. You can try to implement it yourself.