Binary Tree in Action (Construction)

labuladongOriginalAbout 8889 words

This article will resolve

LeetCode	Difficulty
105. Construct Binary Tree from Preorder and Inorder Traversal	🟠
106. Construct Binary Tree from Inorder and Postorder Traversal	🟠
654. Maximum Binary Tree	🟠
889. Construct Binary Tree from Preorder and Postorder Traversal	🟠

Prerequisite Knowledge

Before reading this article, you should first learn:

This article follows Binary Tree Key Ideas (Overview). Let's review the main points for solving binary tree problems:

Note

There are two main ways to solve binary tree problems:

1. Can you get the answer by traversing the binary tree once? If yes, use a traverse function with external variables. This is called the "traversal" approach.

2. Can you define a recursive function that uses the answers of subproblems (subtrees) to get the answer of the original problem? If yes, write this recursive function and use its return value. This is the "divide and conquer" approach.

No matter which way you use, you should think about:

If you take out a single tree node, what should it do? When should it do it (preorder, inorder, postorder)? You don't need to worry about other nodes. The recursive function will handle all nodes for you.

The first article Binary Tree Key Ideas (Thinking) talked about the "traversal" and "divide and conquer" approaches. This article explains construction problems for binary trees.

Most binary tree construction problems use the "divide and conquer" idea: build the whole tree = root node + build left subtree + build right subtree.

Let's look at some problems.

Construct Maximum Binary Tree

Let's start with an easy one. This is LeetCode 654 "Maximum Binary Tree". Here is the problem:

654. Maximum Binary Tree | LeetCode | 🟠

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.
Recursively build the left subtree on the subarray prefix to the left of the maximum value.
Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from nums.

Example 1:

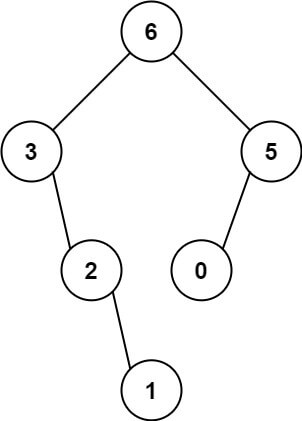
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

Example 2:

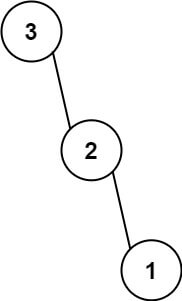
Input: nums = [3,2,1]
Output: [3,null,2,null,1]

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
All integers in nums are unique.

The problem is from LeetCode 654. Maximum Binary Tree.

java

// function signature as follows
TreeNode constructMaximumBinaryTree(int[] nums);

cpp

// The function signature is as follows
TreeNode* constructMaximumBinaryTree(vector<int>& nums);

python

# The function signature is as follows
def constructMaximumBinaryTree(nums: List[int]) -> TreeNode:

// The function signature is as follows
func constructMaximumBinaryTree(nums []int) *TreeNode

javascript

// function signature as follows
var constructMaximumBinaryTree = function(nums) {};

Each binary tree node can be seen as the root of a subtree. For the root, we first need to build the root itself, then build its left and right subtrees.

So, we scan the array to find the maximum value maxVal. This becomes the root node root. Then, we recursively build the left subtree with the subarray to the left of maxVal, and the right subtree with the subarray to the right.

For example, if the input is [3,2,1,6,0,5], the root does this:

java

TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) {
    // find the maximum value in the array
    TreeNode root = new TreeNode(6);
    // recursively construct the left and right subtrees
    root.left = constructMaximumBinaryTree([3,2,1]);
    root.right = constructMaximumBinaryTree([0,5]);
    return root;
}

// the maximum value in the current nums is the root node, and then
// recursively call the left and right arrays to construct the left and right subtrees
// in more detail, the pseudocode is as follows
TreeNode constructMaximumBinaryTree(int[] nums) {
    if (nums is empty) return null;
    // find the maximum value in the array
    int maxVal = Integer.MIN_VALUE;
    int index = 0;
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] > maxVal) {
            maxVal = nums[i];
            index = i;
        }
    }

    TreeNode root = new TreeNode(maxVal);
    // recursively construct the left and right subtrees
    root.left = constructMaximumBinaryTree(nums[0..index-1]);
    root.right = constructMaximumBinaryTree(nums[index+1..nums.length-1]);
    return root;
}

cpp

TreeNode* constructMaximumBinaryTree([3,2,1,6,0,5]) {
    // find the maximum value in the array
    TreeNode* root = new TreeNode(6);
    // recursively construct the left and right subtrees
    root->left = constructMaximumBinaryTree({3,2,1});
    root->right = constructMaximumBinaryTree({0,5});
    return root;
}

// the current maximum value in nums is the root node, and then
// recursively construct the left and right subtrees based on the index
// more specifically, the pseudocode is as follows
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    if (nums.empty()) return nullptr;

    // find the maximum value in the array
    int maxVal = INT_MIN;
    int index = 0;
    for (int i = 0; i < nums.size(); i++) {
        if (nums[i] > maxVal) {
            maxVal = nums[i];
            index = i;
        }
    }

    TreeNode* root = new TreeNode(maxVal);
    // recursively construct the left and right subtrees
    root->left = constructMaximumBinaryTree(nums[0..index-1]);
    root->right = constructMaximumBinaryTree(nums[index+1..nums.size()-1]);
}

python

def constructMaximumBinaryTree([3,2,1,6,0,5]) -> TreeNode:
    # find the maximum value in the array
    root = TreeNode(6)
    # recursively construct the left and right subtrees
    root.left = constructMaximumBinaryTree([3,2,1])
    root.right = constructMaximumBinaryTree([0,5])
    return root

# the current maximum value in nums is the root node, then recursively
# construct the left and right subtrees based on the indices of the subarrays
# in more detail, the pseudocode is as follows
def constructMaximumBinaryTree(nums: List[int]) -> TreeNode:
    if not nums: 
        return None

    # find the maximum value in the array
    maxVal = max(nums)
    index = nums.index(maxVal)

    root = TreeNode(maxVal)
    # recursively construct the left and right subtrees
    root.left = constructMaximumBinaryTree(nums[:index])
    root.right = constructMaximumBinaryTree(nums[index+1:])
    return root

func constructMaximumBinaryTree([3,2,1,6,0,5]) *TreeNode {
    // find the maximum value in the array
    root := &TreeNode{Val: 6}
    // recursively construct left and right subtrees
    root.Left = constructMaximumBinaryTree([]int{3,2,1})
    root.Right = constructMaximumBinaryTree([]int{0,5})
    return root
}

// the current maximum value in nums is the root node, and then
// recursively construct left and right subtrees based on the index
// in more detail, the pseudocode is as follows
func constructMaximumBinaryTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    // find the maximum value in the array
    maxVal := math.MinInt32
    index := 0
    for i := 0; i < len(nums); i++ {
        if nums[i] > maxVal {
            maxVal = nums[i]
            index = i
        }
    }

    root := &TreeNode{Val: maxVal}
    // recursively construct left and right subtrees
    root.Left = constructMaximumBinaryTree(nums[:index])
    root.Right = constructMaximumBinaryTree(nums[index+1:])
    return root
}

javascript

var constructMaximumBinaryTree = function([3,2,1,6,0,5]) {
    // find the maximum value in the array
    var root = new TreeNode(6);
    // recursively construct the left and right subtrees
    root.left = constructMaximumBinaryTree([3,2,1]);
    root.right = constructMaximumBinaryTree([0,5]);
    return root;
}

// the maximum value in the current nums is the root node, then
// recursively construct the left and right subtrees based on the index
// in more detail, it is as follows in pseudocode
var constructMaximumBinaryTree = function(nums) {
    if (nums.length === 0) return null;

    // find the maximum value in the array
    var maxVal = Math.max(...nums);
    var index = nums.indexOf(maxVal);

    var root = new TreeNode(maxVal);
    // recursively construct the left and right subtrees
    root.left = constructMaximumBinaryTree(nums.slice(0, index));
    root.right = constructMaximumBinaryTree(nums.slice(index + 1, nums.length));
    
    return root;
}

The maximum value in nums is the root. Then, recursively build the left and right subtrees using the left and right parts of the array.

With this idea, let's write a helper function build to control the indices:

java

class Solution {

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    // Definition: Construct a tree from nums[lo..hi]
    // that meets the conditions, return the root node
    TreeNode build(int[] nums, int lo, int hi) {
        // base case
        if (lo > hi) {
            return null;
        }

        // Find the maximum value in the array and its corresponding index
        int index = -1, maxVal = Integer.MIN_VALUE;
        for (int i = lo; i <= hi; i++) {
            if (maxVal < nums[i]) {
                index = i;
                maxVal = nums[i];
            }
        }

        // First construct the root node
        TreeNode root = new TreeNode(maxVal);
        // Recursively construct the left and right subtrees
        root.left = build(nums, lo, index - 1);
        root.right = build(nums, index + 1, hi);
        
        return root;
    }
}

cpp

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return build(nums, 0, nums.size()-1);
    }

private:
    // Definition: Construct a tree from nums[lo..hi] that
    // meets the conditions and return the root node
    TreeNode* build(vector<int>& nums, int lo, int hi) {
        // base case
        if (lo > hi) {
            return nullptr;
        }

        // Find the maximum value in the array and its corresponding index
        int index = -1, maxVal = INT_MIN;
        for (int i = lo; i <= hi; i++) {
            if (maxVal < nums[i]) {
                index = i;
                maxVal = nums[i];
            }
        }

        // First, construct the root node
        TreeNode* root = new TreeNode(maxVal);
        // Recursively construct the left and right subtrees
        root->left = build(nums, lo, index - 1);
        root->right = build(nums, index + 1, hi);
        
        return root;
    }
};

python

class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:
        return self.build(nums, 0, len(nums) - 1)

    # Definition: Construct the tree that meets the
    # requirements from nums[lo..hi] and return the root node
    def build(self, nums: List[int], lo: int, hi: int) -> TreeNode:
        # base case
        if lo > hi:
            return None

        # Find the maximum value in the array and its corresponding index
        index = -1
        maxVal = float('-inf')
        for i in range(lo, hi + 1):
            if maxVal < nums[i]:
                index = i
                maxVal = nums[i]

        # First, construct the root node
        root = TreeNode(maxVal)
        # Recursively construct the left and right subtrees
        root.left = self.build(nums, lo, index - 1)
        root.right = self.build(nums, index + 1, hi)
        
        return root

func constructMaximumBinaryTree(nums []int) *TreeNode {
    return build(nums, 0, len(nums) - 1)
}

// Definition: construct a tree with nums[lo..hi]
// that meets the conditions, and return the root node
func build(nums []int, lo, hi int) *TreeNode {
    // base case
    if lo > hi {
        return nil
    }

    // find the maximum value in the array and its corresponding index
    index := -1
    maxVal := -1 << 31
    for i := lo; i <= hi; i++ {
        if maxVal < nums[i] {
            index = i
            maxVal = nums[i]
        }
    }

    // first construct the root node
    root := &TreeNode{Val: maxVal}
    // recursively construct the left and right subtrees
    root.Left = build(nums, lo, index - 1)
    root.Right = build(nums, index + 1, hi)
    
    return root
}

javascript

var constructMaximumBinaryTree = function(nums) {
    return build(nums, 0, nums.length - 1);
}

// Definition: construct a tree from nums[lo..hi]
// that meets the conditions, and return the root node
function build(nums, lo, hi) {
    // base case
    if (lo > hi) {
        return null;
    }

    // find the maximum value in the array and its corresponding index
    let index = -1, maxVal = Number.MIN_SAFE_INTEGER;
    for (let i = lo; i <= hi; i++) {
        if (maxVal < nums[i]) {
            index = i;
            maxVal = nums[i];
        }
    }

    // first, construct the root node
    let root = new TreeNode(maxVal);
    // recursively construct the left and right subtrees
    root.left = build(nums, lo, index - 1);
    root.right = build(nums, index + 1, hi);
    
    return root;
}

Algorithm Visualization

That's it for this problem. It's pretty simple. Now let's look at two harder problems.

Build a Binary Tree from Preorder and Inorder Traversal

LeetCode problem 105 “Construct Binary Tree from Preorder and Inorder Traversal” is a classic question often asked in interviews and written tests:

105. Construct Binary Tree from Preorder and Inorder Traversal | LeetCode | 🟠

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

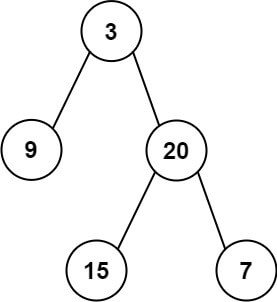
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Constraints:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder and inorder consist of unique values.
Each value of inorder also appears in preorder.
preorder is guaranteed to be the preorder traversal of the tree.
inorder is guaranteed to be the inorder traversal of the tree.

The problem is from LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal.

java

// The function signature is as follows
TreeNode buildTree(int[] preorder, int[] inorder);

cpp

// The function signature is as follows
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder);

python

# the function signature is as follows
def buildTree(preorder: List[int], inorder: List[int]):

// The function signature is as follows
func buildTree(preorder []int, inorder []int) *TreeNode

javascript

// The function signature is as follows
var buildTree = function(preorder, inorder) {};

Let’s get straight to the main idea. First, think about what the root node should do.

Like the previous question, we need to find the value of the root node, build the root, and then use recursion to build the left and right subtrees.

First, let’s review the characteristics of preorder and inorder traversal results.

java

void traverse(TreeNode root) {
    // preorder traversal
    preorder.add(root.val);
    traverse(root.left);
    traverse(root.right);
}

void traverse(TreeNode root) {
    traverse(root.left);
    // inorder traversal
    inorder.add(root.val);
    traverse(root.right);
}

cpp

void traverse(TreeNode* root) {
    if(root == NULL)
        return;
    // pre-order traversal
    preorder.push_back(root->val);
    traverse(root->left);
    traverse(root->right);
}

void traverse(TreeNode* root) {
    if(root == NULL)
        return;
    traverse(root->left);
    // in-order traversal
    inorder.push_back(root->val);
    traverse(root->right);
}

python

def traverse(root):
    if not root:
        return
    # pre-order traversal
    preorder.append(root.val)
    traverse(root.left)
    traverse(root.right)

def traverse(root):
    if not root:
        return
    traverse(root.left)
    # in-order traversal
    inorder.append(root.val)
    traverse(root.right)

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // preorder traversal
    preorder = append(preorder, root.Val)
    traverse(root.Left)
    traverse(root.Right)
}

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.Left)
    // inorder traversal
    inorder = append(inorder, root.Val)
    traverse(root.Right)
}

javascript

var traverse = function(root) {
    if (root === null) {
        return;
    }
    // preorder traversal
    preorder.push(root.val);
    traverse(root.left);
    traverse(root.right);
}

var traverse = function(root) {
    if (root === null) {
        return;
    }
    traverse(root.left);
    // inorder traversal
    inorder.push(root.val);
    traverse(root.right);
}

In the article Binary Tree Frameworks, we discussed how different traversal orders affect the arrangement of elements in the preorder and inorder arrays:

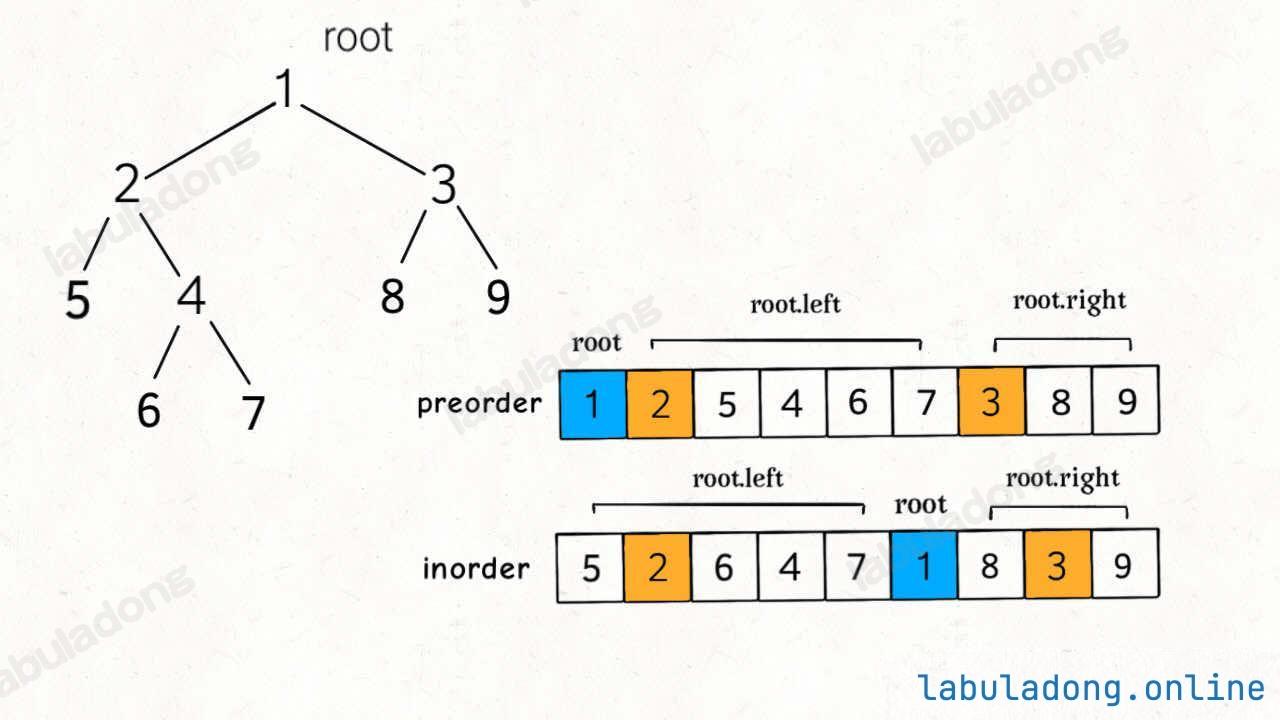
It’s easy to find the root node; the first value in preorder, preorder[0], is the root.

The key is how to use the root value to split the preorder and inorder arrays and build the left and right subtrees.

In other words, what should be put in the ? parts of the following code:

java

TreeNode buildTree(int[] preorder, int[] inorder) {
    // According to the function definition, construct the
    // binary tree using preorder and inorder arrays
    return build(preorder, 0, preorder.length - 1,
                inorder, 0, inorder.length - 1);
}

// Definition of the build function:
// If the preorder traversal array is preorder[preStart..preEnd],
// and the inorder traversal array is inorder[inStart..inEnd],
// construct the binary tree and return its root node
TreeNode build(int[] preorder, int preStart, int preEnd, 
            int[] inorder, int inStart, int inEnd) {
    // The value of the root node corresponds to the first element of the preorder array
    int rootVal = preorder[preStart];
    // The index of rootVal in the inorder array
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }

    TreeNode root = new TreeNode(rootVal);
    // Recursively construct the left and right subtrees
    root.left = build(preorder, ?, ?,
                    inorder, ?, ?);

    root.right = build(preorder, ?, ?,
                    inorder, ?, ?);
    return root;
}

cpp

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    // According to the function definition, construct
    // the binary tree using preorder and inorder
    return build(preorder, 0, preorder.size() - 1,
                inorder, 0, inorder.size() - 1);
}

// Definition of the build function:
// If the preorder traversal array is preorder[preStart..preEnd],
// and the inorder traversal array is inorder[inStart..inEnd],
// build the binary tree and return the root node of the tree
TreeNode* build(vector<int>& preorder, int preStart, int preEnd,
                vector<int>& inorder, int inStart, int inEnd) {
    if (preStart > preEnd) {
        return NULL;
    }
    // The value of the root node is the first element of the preorder traversal array
    int rootVal = preorder[preStart];
    int index;
    for (int i = inStart; i<= inEnd; i++) {
        // The index of rootVal in the inorder traversal array
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }
    TreeNode* root = new TreeNode(rootVal);
    int leftSize = index - inStart;
    // Recursively construct the left and right subtrees
    root->left = build(preorder, ?, ?,
                    inorder, ?, ?);

    root->right = build(preorder, ?, ?,
                    inorder, ?, ?);
    return root;
}

python

def buildTree(preorder, inorder):
    # According to the function definition, use
    # preorder and inorder to construct the binary tree
    return build(preorder, 0, len(preorder) - 1,
                inorder, 0, len(inorder) - 1)

# Definition of build function:
# If the preorder traversal array is preorder[preStart..preEnd],
# and the inorder traversal array is inorder[inStart..inEnd],
# construct the binary tree and return its root node
def build(preorder, preStart, preEnd, 
            inorder, inStart, inEnd):
    # The value of the root node is the first element in the preorder traversal array
    rootVal = preorder[preStart]
    # The index of rootVal in the inorder traversal array
    index = 0
    for i in range(inStart, inEnd + 1):
        if inorder[i] == rootVal:
            index = i
            break

    root = TreeNode(rootVal)
    # Recursively construct the left and right subtrees
    root.left = build(preorder, ?, ?,
                    inorder, ?, ?)

    root.right = build(preorder, ?, ?,
                    inorder, ?, ?)
    return root

func buildTree(preorder []int, inorder []int) *TreeNode {
    // According to the function definition, construct
    // the binary tree using preorder and inorder
    return build(preorder, 0, len(preorder)-1, inorder, 0, len(inorder)-1)
}

// Definition of the build function:
// If the preorder traversal array is preorder[preStart..preEnd],
// and the inorder traversal array is inorder[inStart..inEnd],
// construct the binary tree and return its root node
func build(preorder []int, preStart int, preEnd int, 
           inorder []int, inStart int, inEnd int) *TreeNode {
    if preStart > preEnd {
        return nil
    }
    // The value corresponding to the root node is the first element of the preorder array
    rootVal := preorder[preStart]
    // The index of rootVal in the inorder array
    index := 0
    for i := inStart; i <= inEnd; i++ {
        if inorder[i] == rootVal {
            index = i
            break
        }
    }
    root := &TreeNode{Val: rootVal}
    sizeLeftSubtree := index - inStart
    // Recursively construct the left and right subtrees
    root.Left = build(preorder, ?, ?,
                    inorder, ?, ?)
    root.Right = build(preorder, ?, ?,
                    inorder, ?, ?)
    return root
}

javascript

var buildTree = function(preorder, inorder) {
    // According to the function definition, construct
    // the binary tree using preorder and inorder
    return build(preorder, 0, preorder.length - 1,
                inorder, 0, inorder.length - 1);
}

// Definition of the build function:
// If the preorder traversal array is preorder[preStart..preEnd],
// and the inorder traversal array is inorder[inStart..inEnd],
// construct the binary tree and return the root node of the binary tree
var build = function(preorder, preStart, preEnd, 
                    inorder, inStart, inEnd) {
    // The value corresponding to the root node is the
    // first element of the preorder traversal array
    var rootVal = preorder[preStart];

    // The index of rootVal in the inorder traversal array
    var index = 0;
    for (var i = inStart; i <= inEnd; i++) {
        if (inorder[i] === rootVal) {
            index = i;
            break;
        }
    }

    var root = new TreeNode(rootVal);

    // Recursively construct the left and right subtrees
    root.left = build(preorder, ?, ?,
                    inorder, ?, ?);

    root.right = build(preorder, ?, ?,
                    inorder, ?, ?);

    return root;
}

In the code, the variables rootVal and index correspond to this situation:

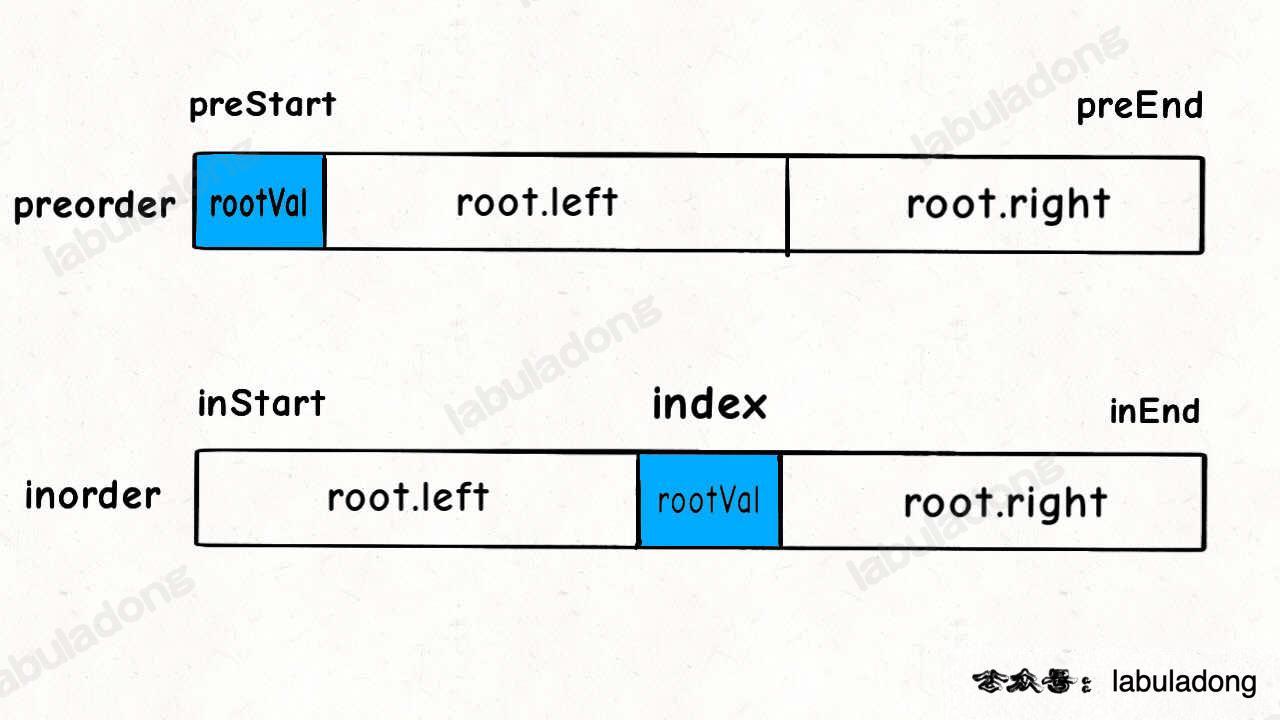
Some readers may notice that using a for loop to find index is not very efficient. It can be improved.

Since the values in the tree are unique, we can use a HashMap to map values to their indexes. Then we can quickly find the index for rootVal:

java

// store the value-to-index mapping in inorder
HashMap<Integer, Integer> valToIndex = new HashMap<>();

public TreeNode buildTree(int[] preorder, int[] inorder) {
    for (int i = 0; i < inorder.length; i++) {
        valToIndex.put(inorder[i], i);
    }
    return build(preorder, 0, preorder.length - 1,
                 inorder, 0, inorder.length - 1);
}

TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {
    int rootVal = preorder[preStart];
    // avoid using a for loop to find rootVal
    int index = valToIndex.get(rootVal);
    // ...
}

cpp

// store the mapping of values to indices in inorder
unordered_map<int, int> valToIndex;

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    for (int i = 0; i < inorder.size(); i++) {
        valToIndex[inorder[i]] = i;
    }
    return build(preorder, 0, preorder.size() - 1,
                 inorder, 0, inorder.size() - 1);
}

TreeNode* build(vector<int>& preorder, int preStart, int preEnd, 
                vector<int>& inorder, int inStart, int inEnd) {
    int rootVal = preorder[preStart];
    // avoid using a for loop to find rootVal
    int index = valToIndex[rootVal];
    // ...
}

python

# store the mapping from values to indices in inorder
val_to_index = {}

def build_tree(preorder, inorder):

    for i in range(len(inorder)):
        val_to_index[inorder[i]] = i

    return build(preorder, 0, len(preorder) - 1,
                 inorder, 0, len(inorder) - 1)

def build(preorder, pre_start, pre_end, 
          inorder, in_start, in_end):
  
    root_val = preorder[pre_start]
    # avoid using for loop to find rootVal
    index = val_to_index[root_val]
    # ...

// store the mapping from values to indices in inorder
valToIndex := make(map[int]int)

func buildTree(preorder []int, inorder []int) *TreeNode {
    for i := 0; i < len(inorder); i++ {
        valToIndex[inorder[i]] = i
    }
    return build(preorder, 0, len(preorder) - 1,
                 inorder, 0, len(inorder) - 1)
}

func build(preorder []int, preStart int, preEnd int,
           inorder []int, inStart int, inEnd int) *TreeNode {
           
    rootVal := preorder[preStart]
    // avoid using a for loop to find rootVal
    index := valToIndex[rootVal]
    // ...
}

javascript

// store the mapping from values to indices in inorder
var valToIndex = {};

var buildTree = function(preorder, inorder) {
    for (var i = 0; i < inorder.length; i++) {
        valToIndex[inorder[i]] = i;
    }
    return build(preorder, 0, preorder.length - 1,
                 inorder, 0, inorder.length - 1);
};

var build = function(preorder, preStart, preEnd, 
               inorder, inStart, inEnd) {
    var rootVal = preorder[preStart];
    // avoid using a for loop to find rootVal
    var index = valToIndex[rootVal];
    // ...
};

Now, let’s look at the diagram and fill in the blanks. What should be filled in for these question marks:

root.left = build(preorder, ?, ?,
                  inorder, ?, ?);

root.right = build(preorder, ?, ?,
                   inorder, ?, ?);

The start and end indexes for the left and right subtrees in the inorder array are easy to figure out:

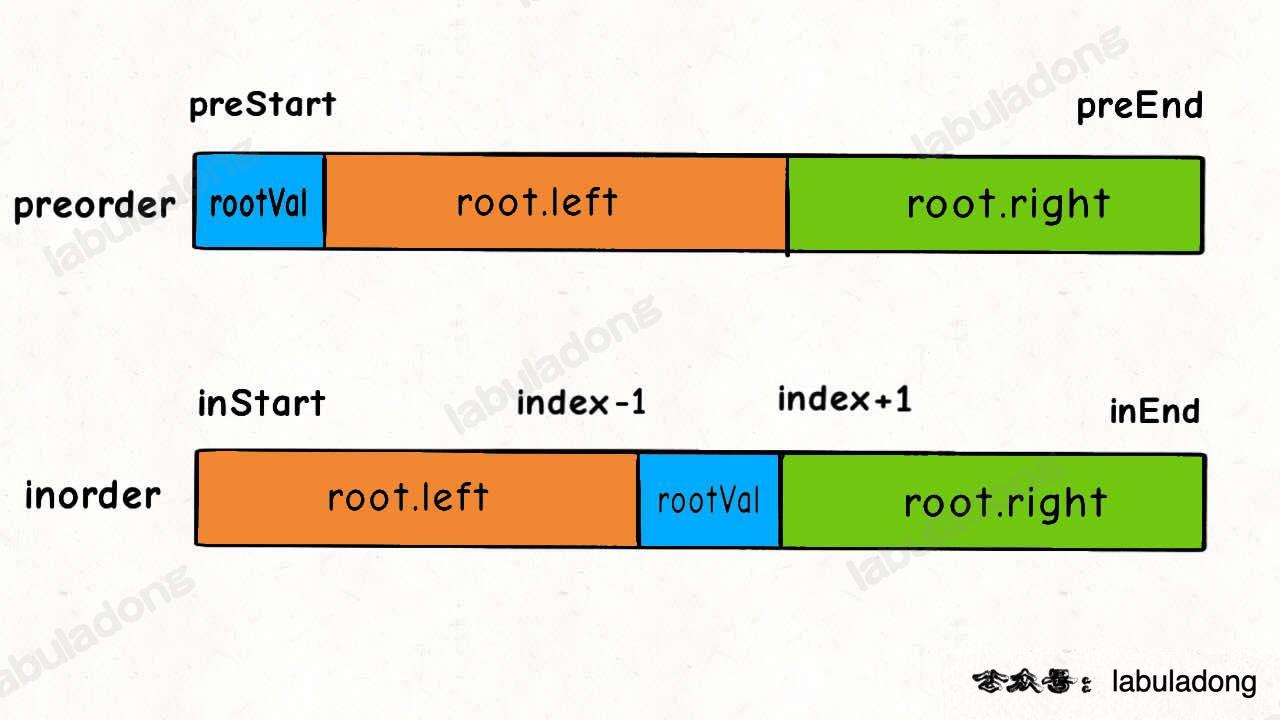
root.left = build(preorder, ?, ?,
                  inorder, inStart, index - 1);

root.right = build(preorder, ?, ?,
                   inorder, index + 1, inEnd);

What about the preorder array? How do we find the start and end indexes for the left and right subtrees?

We can figure this out by counting the number of nodes in the left subtree. Let’s call this number leftSize. Here is how the indexes look in the preorder array:

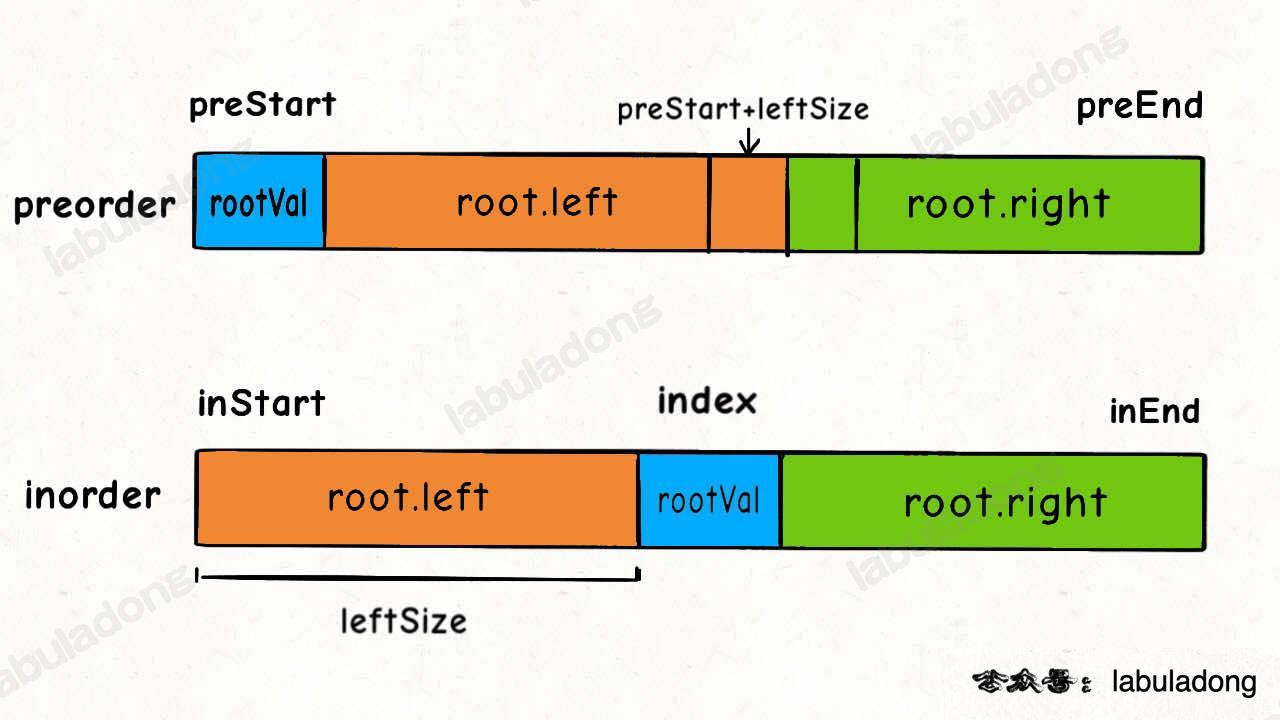
Looking at the diagram, we can write the indexes for the preorder array:

int leftSize = index - inStart;

root.left = build(preorder, preStart + 1, preStart + leftSize,
                  inorder, inStart, index - 1);

root.right = build(preorder, preStart + leftSize + 1, preEnd,
                   inorder, index + 1, inEnd);

Now, the whole algorithm is complete. We just need to add the base case to finish the solution:

java

class Solution {
    // store the mapping of values to indices in inorder
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1,
                    inorder, 0, inorder.length - 1);
    }

    // Definition: the preorder array is preorder[preStart..preEnd]
    // the inorder array is inorder[inStart..inEnd]
    // construct this binary tree and return the root node of the binary tree
    TreeNode build(int[] preorder, int preStart, int preEnd,
                   int[] inorder, int inStart, int inEnd) {
        if (preStart > preEnd) {
            return null;
        }

        // the value of the root node corresponds to the first element of the preorder array
        int rootVal = preorder[preStart];
        // the index of rootVal in the inorder array
        int index = valToIndex.get(rootVal);

        int leftSize = index - inStart;

        // first, construct the current root node
        TreeNode root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                inorder, inStart, index - 1);

        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                inorder, index + 1, inEnd);
        return root;
    }
}

cpp

class Solution {
public:
    // store the mapping from value to index in inorder
    unordered_map<int, int> valToIndex;

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        for (int i = 0; i < inorder.size(); i++) {
            valToIndex[inorder[i]] = i;
        }
        return build(preorder, 0, preorder.size() - 1,
                    inorder, 0, inorder.size() - 1);
    }

    // definition of build function:
    // if the preorder array is preorder[preStart..preEnd],
    // and the inorder array is inorder[inStart..inEnd],
    // construct the binary tree and return its root node
    TreeNode* build(vector<int>& preorder, int preStart, int preEnd, 
                    vector<int>& inorder, int inStart, int inEnd) {

        if (preStart > preEnd) {
            return NULL;
        }

        // the value of the root node is the first element of the preorder array
        int rootVal = preorder[preStart];
        // the index of rootVal in the inorder array
        int index = valToIndex[rootVal];

        int leftSize = index - inStart;

        // first construct the current root node
        TreeNode* root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        root->left = build(preorder, preStart + 1, preStart + leftSize,
                        inorder, inStart, index - 1);

        root->right = build(preorder, preStart + leftSize + 1, preEnd,
                        inorder, index + 1, inEnd);
        return root;
    }
};

python

class Solution:
    # store the mapping from values in inorder to their indices
    valToIndex = dict()

    def buildTree(self, preorder, inorder):
        for i in range(len(inorder)):
            self.valToIndex[inorder[i]] = i
        return self.build(preorder, 0, len(preorder) - 1,
                          inorder, 0, len(inorder) - 1)

    # definition of the build function:
    # if the preorder traversal array is preorder[preStart..preEnd],
    # and the inorder traversal array is inorder[inStart..inEnd],
    # construct the binary tree and return its root node
    def build(self, preorder, preStart, preEnd,
               inorder, inStart, inEnd):
        if preStart > preEnd:
            return None

        # the root node's value is the first element in the preorder array
        rootVal = preorder[preStart]
        # the index of rootVal in the inorder array
        index = self.valToIndex[rootVal]

        leftSize = index - inStart

        # first construct the current root node
        root = TreeNode(rootVal) 

        # recursively construct the left and right subtrees
        root.left = self.build(preorder, preStart + 1, preStart + leftSize,
                               inorder, inStart, index - 1)

        root.right = self.build(preorder, preStart + leftSize + 1, preEnd,
                                inorder, index + 1, inEnd)

        return root

func buildTree(preorder []int, inorder []int) *TreeNode {
    valToIndex := make(map[int]int)
    for i := 0; i < len(inorder); i++ {
        valToIndex[inorder[i]] = i
    }

    var build func([]int, int, int, []int, int, int) *TreeNode
    build = func(preorder []int, preStart, preEnd int, inorder []int, inStart, inEnd int) *TreeNode {
        if preStart > preEnd {
            return nil
        }

        // the value corresponding to the root node is the first element of the preorder array
        rootVal := preorder[preStart]
        // the index of rootVal in the inorder array
        index := valToIndex[rootVal]
        leftSize := index - inStart

        // first construct the current root node
        root := &TreeNode{Val: rootVal}
        // recursively construct the left and right subtrees
        root.Left = build(preorder, preStart+1, preStart+leftSize, inorder, inStart, index-1)
        root.Right = build(preorder, preStart+leftSize+1, preEnd, inorder, index+1, inEnd)
        return root
    }

    return build(preorder, 0, len(preorder)-1, inorder, 0, len(inorder)-1)
}

javascript

var buildTree = function(preorder, inorder) {
    // store the mapping from value to index in inorder
    var valToIndex = new Map();

    for (let i = 0; i < inorder.length; i++) {
        valToIndex.set(inorder[i], i);
    }
    return build(preorder, 0, preorder.length - 1,
                inorder, 0, inorder.length - 1);

    // definition of build function:
    // if the preorder array is preorder[preStart..preEnd],
    // and the inorder array is inorder[inStart..inEnd],
    // construct the binary tree and return its root node
    function build(preorder, preStart, preEnd, 
               inorder, inStart, inEnd) {

        if (preStart > preEnd) {
            return null;
        }

        // the value of the root node is the first element of the preorder array
        var rootVal = preorder[preStart];
        // the index of rootVal in the inorder array
        var index = valToIndex.get(rootVal);

        var leftSize = index - inStart;

        // first construct the current root node
        var root = new TreeNode(rootVal);
        // recursively build the left and right subtrees
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                        inorder, inStart, index - 1);

        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                        inorder, index + 1, inEnd);
        return root;
    }
};

The main function only needs to call the buildTree function. The solution may look long and the function has many parameters, but all these parameters do is control the range in the arrays. Drawing a diagram makes everything clear.

Build a Binary Tree from Postorder and Inorder Traversal

This problem is similar to the previous one. This time, we use the postorder and inorder traversal arrays to build a binary tree. This is LeetCode Problem 106: Construct Binary Tree from Inorder and Postorder Traversal:

106. Construct Binary Tree from Inorder and Postorder Traversal | LeetCode | 🟠

Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

Example 1:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: inorder = [-1], postorder = [-1]
Output: [-1]

Constraints:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder and postorder consist of unique values.
Each value of postorder also appears in inorder.
inorder is guaranteed to be the inorder traversal of the tree.
postorder is guaranteed to be the postorder traversal of the tree.

The problem is from LeetCode 106. Construct Binary Tree from Inorder and Postorder Traversal.

java

// The function signature is as follows
TreeNode buildTree(int[] inorder, int[] postorder);

cpp

// The function signature is as follows
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder);

python

# The function signature is as follows
def buildTree(inorder: List[int], postorder: List[int]) -> TreeNode:

// The function signature is as follows
func buildTree(inorder []int, postorder []int) *TreeNode

javascript

// The function signature is as follows
var buildTree = function(inorder, postorder) {}

Let's look at the features of postorder and inorder traversals:

java

void traverse(TreeNode root) {
    traverse(root.left);
    traverse(root.right);
    // postorder traversal
    postorder.add(root.val);
}

void traverse(TreeNode root) {
    traverse(root.left);
    // inorder traversal
    inorder.add(root.val);
    traverse(root.right);
}

cpp

void traverse(TreeNode* root) {
    if (root == NULL) return;
  
    traverse(root->left);
    traverse(root->right);
    
    // postorder traversal
    postorder.push_back(root->val);
}

void traverse(TreeNode* root) {
    if (root == NULL) return;
    
    traverse(root->left);
    
    // inorder traversal
    inorder.push_back(root->val);
    
    traverse(root->right);
}

python

def traverse(root):
    if root:
        traverse(root.left)
        traverse(root.right)
        # postorder traversal
        postorder.append(root.val)

def traverse(root):
    if root:
        traverse(root.left)
        # inorder traversal
        inorder.append(root.val)
        traverse(root.right)

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.Left)
    traverse(root.Right)
    // postorder traversal
    postorder = append(postorder, root.Val)
}

func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.Left)
    // inorder traversal
    inorder = append(inorder, root.Val)
    traverse(root.Right)
}

javascript

var traverse = function(root) {
    if (root==null) { 
      return; 
    }
    traverse(root.left);
    traverse(root.right);
    // post-order traversal
    postorder.push(root.val);
}

var traverse = function(root) {
    if (root==null) { 
      return; 
    }
    traverse(root.left);
    // in-order traversal
    inorder.push(root.val);
    traverse(root.right);
}

Because of the difference in traversal orders, the elements in the postorder and inorder arrays have the following layout:

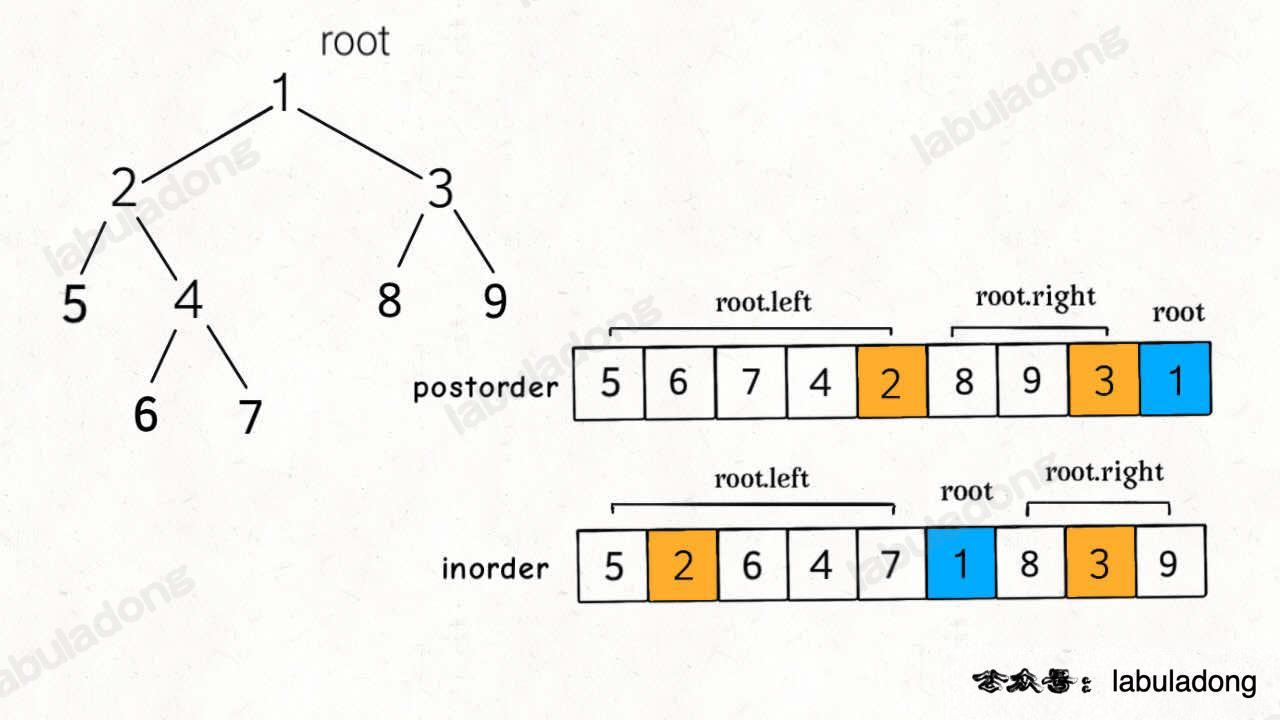
The key difference from the previous problem is that postorder is the opposite of preorder, so the root node is the last element in the postorder array.

The overall algorithm structure is very similar to the previous problem. We still write a helper function called build:

java

class Solution {
    // Store the mapping from values to indices in the inorder array
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(inorder, 0, inorder.length - 1,
                    postorder, 0, postorder.length - 1);
    }

    // Definition of the build function:
    // The postorder traversal array is postorder[postStart..postEnd],
    // The inorder traversal array is inorder[inStart..inEnd],
    // Construct the binary tree and return its root node
    TreeNode build(int[] inorder, int inStart, int inEnd,
                int[] postorder, int postStart, int postEnd) {
        // The value of the root node is the last element of the postorder traversal array
        int rootVal = postorder[postEnd];
        // The index of rootVal in the inorder traversal array
        int index = valToIndex.get(rootVal);

        TreeNode root = new TreeNode(rootVal);
        // Recursively construct the left and right subtrees
        root.left = build(inorder, ?, ?,
                        postorder, ?, ?);

        root.right = build(inorder, ?, ?,
                        postorder, ?, ?);
        return root;
    }
}

cpp

class Solution {
public:
    // store the mapping from value to index in inorder
    unordered_map<int, int> valToIndex;

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        for (int i = 0; i < inorder.size(); i++) {
            valToIndex[inorder[i]] = i;
        }
        return build(inorder, 0, inorder.size() - 1,
                     postorder, 0, postorder.size() - 1);
    }

// definition of build function:
// postorder traversal array is postorder[postStart..postEnd],
// inorder traversal array is inorder[inStart..inEnd],
// construct the binary tree, return the root node of the tree
TreeNode* build(vector<int>& inorder, int inStart, int inEnd,
                vector<int>& postorder, int postStart, int postEnd) {
        // the value of the root node is the last element in the postorder array
        int rootVal = postorder[postEnd];
        // index of rootVal in the inorder array
        int index = valToIndex[rootVal];

        TreeNode* root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        root->left = build(inorder, ?, ?,
                           postorder, ?, ?);

        root->right = build(inorder, ?, ?,
                            postorder, ?, ?);
        return root;
    }
};

python

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        # store the mapping from value to index in inorder
        valToIndex = {val: idx for idx, val in enumerate(inorder)}

        # definition of build function:
        # postorder traversal array is postorder[postStart..postEnd],
        # inorder traversal array is inorder[inStart..inEnd],
        # construct the binary tree, return the root node of this tree
        def build(in_left, in_right, post_left, post_right):
            if in_left > in_right: return
            
            # the value of the root node is the last element of the postorder traversal array
            root_val = postorder[post_right]
            # the index of rootVal in the inorder traversal array
            index = valToIndex[root_val]

            root = TreeNode(root_val)
            # recursively construct the left and right subtrees
            size_left_subtree = index - in_left
            root.left = build(inorder, ?, ?,
                               postorder, ?, ?)
            root.right = build(inorder, ?, ?,
                                postorder, ?, ?)
            
            return root

        return build(0, len(inorder) - 1, 0, len(postorder) - 1)

func buildTree(inorder []int, postorder []int) *TreeNode {
    // store the mapping from value to index in inorder
    valToIndex := make(map[int]int)
    for i, v := range inorder {
        valToIndex[v] = i
    }

    // definition of build function:
    // postorder array is postorder[postStart..postEnd],
    // inorder array is inorder[inStart..inEnd],
    // construct the binary tree, return the root node of the tree
    var build func(inStart int, inEnd int, postStart int, postEnd int) *TreeNode
    build = func(inStart int, inEnd int, postStart int, postEnd int) *TreeNode {
        if inStart > inEnd {
            return nil
        }

        // the value of root node is the last element of postorder array
        rootVal := postorder[postEnd]
        // index of rootVal in inorder array
        index := valToIndex[rootVal]

        root := &TreeNode{Val: rootVal}
        // recursively construct the left and right subtrees
        root.Left = build(inorder, ?, ?,
                           postorder, ?, ?);
        root.Right = build(inorder, ?, ?,
                            postorder, ?, ?);

        return root
    }

    return build(0, len(inorder)-1, 0, len(postorder)-1)
}

javascript

var buildTree = function(inorder, postorder) {
    // store the mapping of values to indices in inorder
    var valToIndex = {};
    for (let i = 0; i < inorder.length; i++) {
        valToIndex[inorder[i]] = i;
    }

    // definition of the build function:
    // the postorder traversal array is postorder[postStart..postEnd],
    // the inorder traversal array is inorder[inStart..inEnd],
    // construct the binary tree and return the root node of this tree
    function build(inStart, inEnd, postStart, postEnd) {
        // if no elements to construct subtrees
        if (inStart > inEnd) {
            return null; 
        }

        // the value of the root node is the last element in the postorder traversal array
        let rootVal = postorder[postEnd];
        // the index of rootVal in the inorder traversal array
        let index = valToIndex[rootVal];
        
        var root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        root.left = build(inorder, ?, ?,
                           postorder, ?, ?);
        root.right = build(inorder, ?, ?,
                           postorder, ?, ?);
        
        return root;
    }
    return build(0, inorder.length - 1, 0, postorder.length - 1);
};

Now, the status of postorder and inorder is as follows:

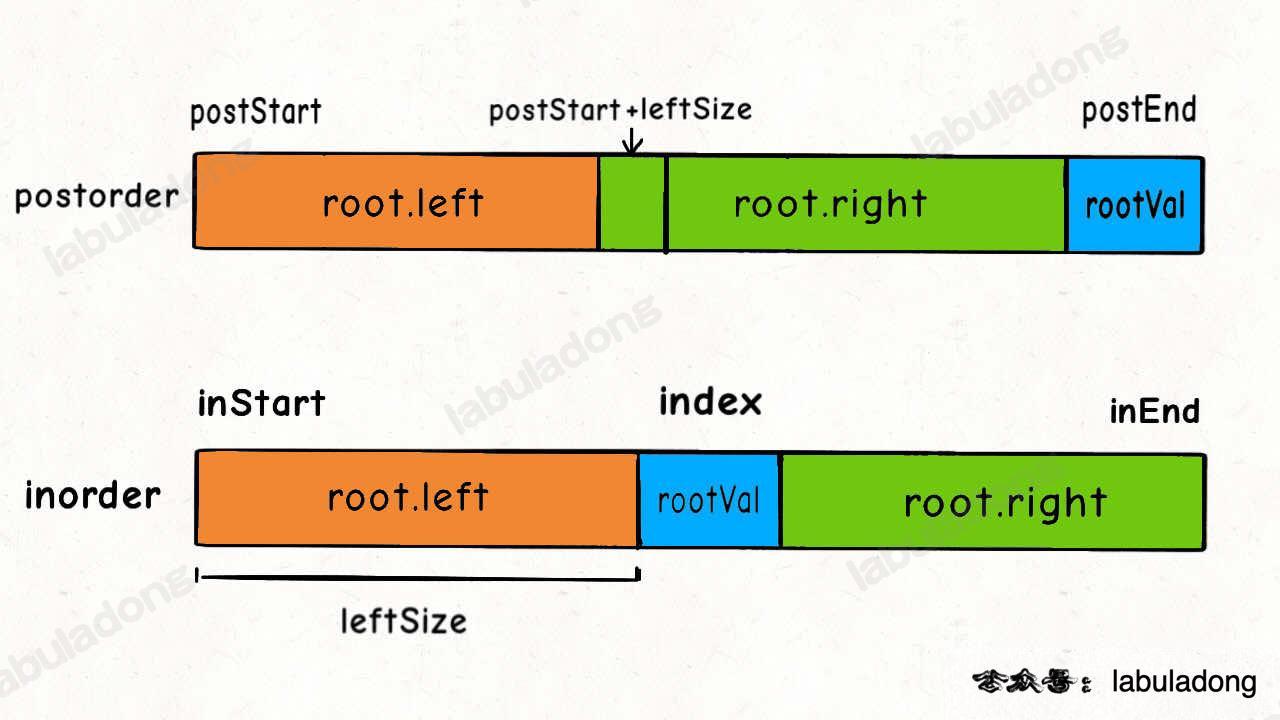
We can fill in the missing indices as shown above:

int leftSize = index - inStart;

root.left = build(inorder, inStart, index - 1,
                  postorder, postStart, postStart + leftSize - 1);

root.right = build(inorder, index + 1, inEnd,
                   postorder, postStart + leftSize, postEnd - 1);

Here is the complete solution code:

java

class Solution {
    // store the mapping from value to index in inorder
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(inorder, 0, inorder.length - 1,
                    postorder, 0, postorder.length - 1);
    }

    // Definition: the inorder array is inorder[inStart..inEnd],
    // the postorder array is postorder[postStart..postEnd],
    // the build function constructs this binary tree
    // and returns the root node of the binary tree
    TreeNode build(int[] inorder, int inStart, int inEnd,
                int[] postorder, int postStart, int postEnd) {

        if (inStart > inEnd) {
            return null;
        }
        // the value of the root node is the last element in the postorder array
        int rootVal = postorder[postEnd];
        // the index of rootVal in the inorder array
        int index = valToIndex.get(rootVal);
        // the number of nodes in the left subtree
        int leftSize = index - inStart;
        TreeNode root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        root.left = build(inorder, inStart, index - 1,
                         postorder, postStart, postStart + leftSize - 1);
        
        root.right = build(inorder, index + 1, inEnd,
                          postorder, postStart + leftSize, postEnd - 1);
        return root;
    }
}

cpp

class Solution {
    // store the mapping from value to index in inorder
    unordered_map<int, int> valToIndex;

public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        for (int i = 0; i < inorder.size(); i++) {
            valToIndex[inorder[i]] = i;
        }
        return build(inorder, 0, inorder.size() - 1,
                     postorder, 0, postorder.size() - 1);
    }

    // Definition: the inorder array is inorder[inStart..inEnd],
    // the postorder array is postorder[postStart..postEnd],
    // the build function constructs this binary tree
    // and returns the root node of the binary tree
    TreeNode* build(vector<int>& inorder, int inStart, int inEnd,
                    vector<int>& postorder, int postStart, int postEnd) {

        if (inStart > inEnd) {
            return nullptr;
        }
        // the value of the root node is the last element in the postorder array
        int rootVal = postorder[postEnd];
        // the index of rootVal in the inorder array
        int index = valToIndex[rootVal];
        // the number of nodes in the left subtree
        int leftSize = index - inStart;
        TreeNode* root = new TreeNode(rootVal);

        // recursively construct the left and right subtrees
        root->left = build(inorder, inStart, index - 1,
                           postorder, postStart, postStart + leftSize - 1);
        
        root->right = build(inorder, index + 1, inEnd,
                            postorder, postStart + leftSize, postEnd - 1);
        return root;
    }
};

python

class Solution:
    # store the mapping from value to index in inorder
    val_to_index = {}

    def buildTree(self, inorder, postorder):
        for i in range(len(inorder)):
            self.val_to_index[inorder[i]] = i
        return self.build(inorder, 0, len(inorder) - 1,
                          postorder, 0, len(postorder) - 1)

    # Definition: the inorder array is inorder[inStart..inEnd],
    # the postorder array is postorder[postStart..postEnd],
    # the build function constructs this binary tree
    # and returns the root node of the binary tree
    def build(self, inorder, in_start, in_end,
              postorder, post_start, post_end):

        if in_start > in_end:
            return None
        # the value of the root node is the last element in the postorder array
        root_val = postorder[post_end]
        # the index of rootVal in the inorder array
        index = self.val_to_index[root_val]
        # the number of nodes in the left subtree
        left_size = index - in_start
        root = TreeNode(root_val) 
        # recursively construct the left and right subtrees
        root.left = self.build(inorder, in_start, index - 1,
                               postorder, post_start, post_start + left_size - 1)
        
        root.right = self.build(inorder, index + 1, in_end,
                                postorder, post_start + left_size, post_end - 1)
        return root

func buildTree(inorder []int, postorder []int) *TreeNode {
    // store the mapping from value to index in inorder
    indexMap := make(map[int]int)
    for i, v := range inorder {
        indexMap[v] = i
    }
    return build(inorder, 0, len(inorder)-1, postorder, 0, len(postorder)-1, indexMap)
}


// Definition of the build function:
// The postorder traversal array is postorder[postStart..postEnd],
// The inorder traversal array is inorder[inStart..inEnd],
// Construct the binary tree and return its root node.
func build(inorder []int, inStart int, inEnd int, postorder []int, postStart int, postEnd int, indexMap map[int]int) *TreeNode {
    if inStart > inEnd {
        return nil
    }
    // the value of the root node is the last element in the postorder array
    rootVal := postorder[postEnd]
    // the index of rootVal in the inorder array
    index := indexMap[rootVal]
    // the number of nodes in the left subtree
    leftSize := index - inStart
    
    root := &TreeNode{Val: rootVal}
    // recursively construct the left and right subtrees
    root.Left = build(inorder, inStart, index-1, postorder, postStart, postStart+leftSize-1, indexMap)
    root.Right = build(inorder, index+1, inEnd, postorder, postStart+leftSize, postEnd-1, indexMap)
    
    return root
}

javascript

var buildTree = function(inorder, postorder) {
    // store the mapping from value to index in inorder
    let valToIndex = new Map();
    for (let i = 0; i < inorder.length; i++) {
        valToIndex.set(inorder[i], i);
    }

    // Definition: the inorder array is inorder[inStart..inEnd],
    // the postorder array is postorder[postStart..postEnd],
    // the build function constructs this binary tree
    // and returns the root node of the binary tree
    var build = function(inorder, inStart, inEnd, postorder, postStart, postEnd) {
        if (inStart > inEnd) {
            return null;
        }
        // the value of the root node is the last element in the postorder array
        let rootVal = postorder[postEnd];
        // the index of rootVal in the inorder array
        let index = valToIndex.get(rootVal);
        // the number of nodes in the left subtree
        let leftSize = index - inStart;
        let root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        root.left = build(inorder, inStart, index - 1, postorder, postStart, postStart + leftSize - 1);
        root.right = build(inorder, index + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);
        return root;
    }

    return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
};

Algorithm Visualization

With the foundation from the previous problem, this one is easy to solve. The only difference is that rootVal is now the last element, and we need to adjust the function parameters a bit. As long as you understand the features of a binary tree, this problem is not hard to write.

Constructing a Binary Tree from Preorder and Postorder Traversal

This is LeetCode Problem 889: Construct Binary Tree from Preorder and Postorder Traversal. You are given the preorder and postorder traversal of a binary tree. Your task is to restore the structure of the binary tree.

The function signature is:

java

TreeNode constructFromPrePost(int[] preorder, int[] postorder);

cpp

TreeNode* constructFromPrePost(vector<int>& preOrder, vector<int>& postOrder);

python

from typing import List

def constructFromPrePost(preorder: List[int], postorder: List[int]) -> TreeNode:

func constructFromPrePost(preorder []int, postorder []int) *TreeNode

javascript

var constructFromPrePost = function(preorder, postorder) {}

This problem is different from the previous two:

Given preorder and inorder, or postorder and inorder traversal, you can restore the unique original binary tree. But with preorder and postorder, you cannot restore a unique tree.

The problem also says, if there are multiple possible answers, you can return any of them.

Why is that? As we said before, the usual way to build a binary tree is simple: find the root node, then find and build the left and right subtrees recursively.

In the previous two problems, you could use preorder or postorder to find the root, then use inorder to know the left and right subtrees (the problem says all values are unique).

In this problem, you can find the root, but you cannot know exactly which nodes belong to the left or right subtrees.

For example, given this input:

preorder = [1,2,3], postorder = [3,2,1]

Both of the following trees fit the condition, but their structures are different:

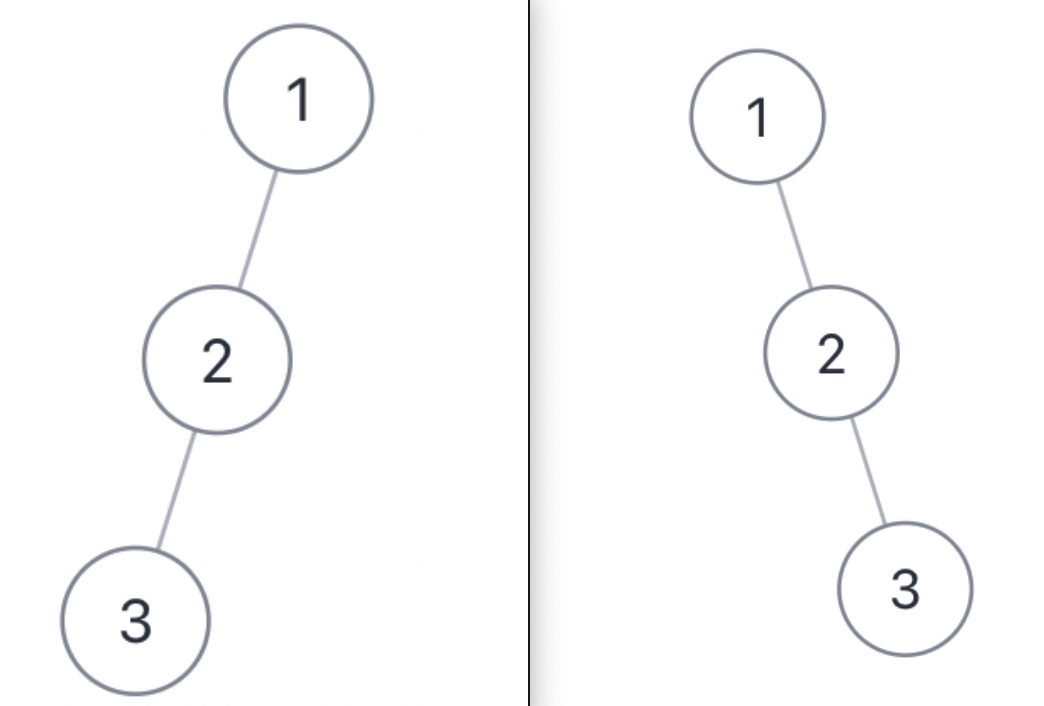
However, the logic to restore the tree from preorder and postorder is not much different from the previous problems. You still use the indexes of left and right subtrees to build the tree:

1. First, take the first element of preorder or the last element of postorder as the root.

2. Then, take the second element of preorder as the root of the left subtree.

3. In postorder, find the index of the left subtree's root, so you know the boundary for the left subtree, and then for the right subtree. Build the left and right subtrees recursively.

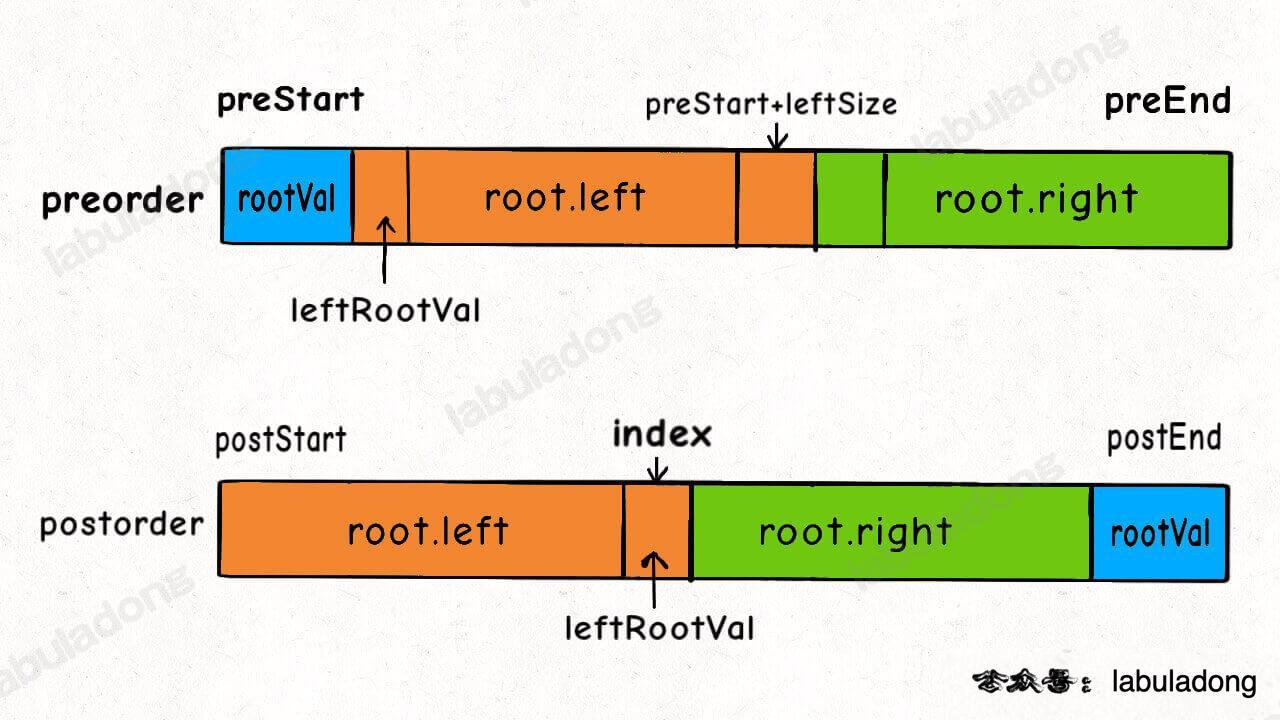
For details, see the code.

java

class Solution {
    // store the mapping of values to indices in postorder
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        for (int i = 0; i < postorder.length; i++) {
            valToIndex.put(postorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1,
                    postorder, 0, postorder.length - 1);
    }

    // definition: construct a binary tree based on
    // preorder[prestart..preend] and postorder[poststart..postend]
    // and return the root node.
    TreeNode build(int[] preorder, int preStart, int preEnd,
                   int[] postorder, int postStart, int postEnd) {
        if (preStart > preEnd) {
            return null;
        }
        if (preStart == preEnd) {
            return new TreeNode(preorder[preStart]);
        }

        // the value of the root node corresponds to the first element in the preorder array
        int rootVal = preorder[preStart];
        // the value of root.left is the second element in the preorder array
        // the key to constructing the binary tree from preorder and
        // postorder traversals is determining the left subtree's root node
        // and the element ranges of the left and right subtrees in preorder and postorder
        int leftRootVal = preorder[preStart + 1];
        // the index of leftrootval in the postorder array
        int index = valToIndex.get(leftRootVal);
        // the number of elements in the left subtree
        int leftSize = index - postStart + 1;

        // first, construct the current root node
        TreeNode root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        // derive the index boundaries of the left and right subtrees based on
        // the left subtree's root node index and the number of elements
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                postorder, postStart, index);
        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                postorder, index + 1, postEnd - 1);

        return root;
    }
}

cpp

class Solution {
    // store the mapping of values to indices in postorder
    unordered_map<int, int> valToIndex;

public:
    TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
        for (int i = 0; i < postorder.size(); i++) {
            valToIndex[postorder[i]] = i;
        }
        return build(preorder, 0, preorder.size() - 1,
                    postorder, 0, postorder.size() - 1);
    }

    // Definition: construct a binary tree based on
    // preorder[preStart..preEnd] and postorder[postStart..postEnd]
    // and return the root node.
    TreeNode* build(vector<int>& preorder, int preStart, int preEnd,
                   vector<int>& postorder, int postStart, int postEnd) {
        if (preStart > preEnd) {
            return nullptr;
        }
        if (preStart == preEnd) {
            return new TreeNode(preorder[preStart]);
        }

        // the value of the root node corresponds to the first element of the preorder array
        int rootVal = preorder[preStart];
        // root.left's value is the second element of the preorder array
        // the key to constructing a binary tree using preorder and postorder is
        // to determine the element range of the left and right subtrees
        // in preorder and postorder based on the root node of the left subtree
        int leftRootVal = preorder[preStart + 1];
        // the index of leftRootVal in the postorder array
        int index = valToIndex[leftRootVal];
        // the number of elements in the left subtree
        int leftSize = index - postStart + 1;

        // first construct the current root node
        TreeNode* root = new TreeNode(rootVal);
        // recursively construct the left and right subtrees
        // deduce the index boundaries of the left and right subtrees based on the
        // root node index and the number of elements of the left subtree
        root->left = build(preorder, preStart + 1, preStart + leftSize,
                postorder, postStart, index);
        root->right = build(preorder, preStart + leftSize + 1, preEnd,
                postorder, index + 1, postEnd - 1);

        return root;
    }
};

python

class Solution:
    # store the mapping from value to index in postorder
    valToIndex = dict()

    def constructFromPrePost(self, preorder, postorder):
        for i in range(len(postorder)):
            self.valToIndex[postorder[i]] = i
        return self.build(preorder, 0, len(preorder) - 1,
                          postorder, 0, len(postorder) - 1)

    # definition: construct the binary tree based on
    # preorder[preStart..preEnd] and postorder[postStart..postEnd]
    # build the binary tree and return the root node.
    def build(self, preorder, preStart, preEnd,
              postorder, postStart, postEnd):
        if preStart > preEnd:
            return None
        if preStart == preEnd:
            return TreeNode(preorder[preStart])

        # the value of the root node is the first element in the preorder array
        rootVal = preorder[preStart]
        # the value of root.left is the second element in preorder
        # the key to constructing the binary tree using preorder and postorder is to determine the
        # element range of the left and right subtrees using the root node of the left subtree
        # determine the element range of the left and right subtrees in preorder and postorder
        leftRootVal = preorder[preStart + 1]
        # the index of leftRootVal in the postorder array
        index = self.valToIndex[leftRootVal]
        # the number of elements in the left subtree
        leftSize = index - postStart + 1
     
        # first construct the current root node
        root = TreeNode(rootVal) 
        # recursively construct the left and right subtrees
        # derive the index boundaries of the left and right subtrees based on the
        # root node index and the number of elements in the left subtree
        root.left = self.build(preorder, preStart + 1, preStart + leftSize,
                               postorder, postStart, index)
        root.right = self.build(preorder, preStart + leftSize + 1, preEnd,
                                postorder, index + 1, postEnd - 1)

        return root

func constructFromPrePost(preorder []int, postorder []int) *TreeNode{
    // store the mapping from values to indices in postorder
    valToIndex := make(map[int]int)

    for i := 0; i < len(postorder); i++ {
        valToIndex[postorder[i]] = i
    }

    // definition: build a binary tree based on
    // preorder[preStart..preEnd] and postorder[postStart..postEnd], and return the root node
    var build func(preorder []int, preStart, preEnd int, postorder []int, postStart, postEnd int) *TreeNode
	build = func(preorder []int, preStart, preEnd int, postorder []int, postStart, postEnd int) *TreeNode {    
    	if preStart > preEnd {
        	return nil
    	}
    	if preStart == preEnd {
        	return &TreeNode{
				Val:   preorder[preStart],
				Left:  nil,
				Right: nil,
			}
    	}

    	// the value of the root node corresponds to the first element in the preorder array
    	rootVal := preorder[preStart]
    	// the value of root.left is the second element in the preorder array
    	// the key to constructing a binary tree from preorder and postorder traversals is
// determining the element ranges of the left and right subtrees via the root node of the left subtree
    	// determine the element ranges of the left and right subtrees in preorder and postorder
    	leftRootVal := preorder[preStart + 1]
    	// the index of leftRootVal in the postorder array
    	index := valToIndex[leftRootVal]
    	// the number of elements in the left subtree
    	leftSize := index - postStart + 1

    	// first construct the current root node
    	root := &TreeNode{
			Val:   rootVal,
			Left:  nil,
			Right: nil,
		}

    	// recursively construct the left and right subtrees
    	// deduce the index boundaries of the left and right subtrees based on
// the root node index and the number of elements in the left subtree
    	root.Left = build(preorder, preStart + 1, preStart + leftSize, postorder, postStart, index)
    	root.Right = build(preorder, preStart + leftSize + 1, preEnd, postorder, index + 1, postEnd - 1)

    	return root
    }

    return build(preorder, 0, len(preorder) - 1, postorder, 0, len(postorder) - 1)
}

javascript

var constructFromPrePost = function(preorder, postorder) {
    // store the mapping from values to indices in postorder

    const valToIndex = {};
    for (let i = 0; i < postorder.length; i++) {
        valToIndex[postorder[i]] = i;
    }

// definition: build the binary tree based on
// preorder[preStart..preEnd] and postorder[postStart..postEnd] and return the root node
var build = function(preorder, preStart, preEnd, postorder, postStart, postEnd) {
    if (preStart > preEnd) {
        return null;
    }
    if (preStart === preEnd) {
        return new TreeNode(preorder[preStart]);
    }

    // the value of the root node corresponds to the first element of the preorder array
    let rootVal = preorder[preStart];
    // the value of root.left is the second element of the preorder array
    // the key to constructing the binary tree through preorder and
    // postorder traversal lies in the root node of the left subtree
    // determine the element ranges of the left and right subtrees in preorder and postorder
    let leftRootVal = preorder[preStart + 1];
    // the index of leftRootVal in the postorder array
    let index = valToIndex[leftRootVal];
    // the number of elements in the left subtree
    let leftSize = index - postStart + 1;

    // first, construct the current root node
    let root = new TreeNode(rootVal);
    // recursively construct the left and right subtrees
    // deduce the index boundaries of the left and right subtrees based on
    // the root node index and the number of elements of the left subtree
    root.left = build(preorder, preStart + 1, preStart + leftSize,
            postorder, postStart, index);
    root.right = build(preorder, preStart + leftSize + 1, preEnd,
            postorder, index + 1, postEnd - 1);

    return root;
};

    return build(preorder, 0, preorder.length - 1,
                    postorder, 0, postorder.length - 1);
};

Algorithm Visualization

The code is very similar to the previous two problems. While reading the code, you can think about why the answer is not unique with preorder and postorder.

The key part is this line:

int leftRootVal = preorder[preStart + 1];

We assume the second element in preorder is the root of the left subtree. But actually, the left subtree could be empty, then this element is the root of the right subtree. Since we can't know for sure, the answer is not unique.

Now, we have solved the problem of restoring a binary tree from preorder and postorder traversal.

To sum up, constructing a binary tree usually uses the "divide the problem" idea: build the whole tree = root node + build left subtree + build right subtree. First find the root, then use the root's value to find the left and right subtree elements, then build them recursively.

Do you understand the trick now?

Related Problems

You can install my Chrome extension then open the link.

LeetCode	Difficulty
1008. Construct Binary Search Tree from Preorder Traversal	🟠

Binary Tree in Action (Construction)

105. Construct Binary Tree from Preorder and Inorder Traversal https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal

106. Construct Binary Tree from Inorder and Postorder Traversal https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal

654. Maximum Binary Tree https://leetcode.com/problems/maximum-binary-tree

889. Construct Binary Tree from Preorder and Postorder Traversal https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal

Construct Maximum Binary Tree

Build a Binary Tree from Preorder and Inorder Traversal

Build a Binary Tree from Postorder and Inorder Traversal

Constructing a Binary Tree from Preorder and Postorder Traversal