Binary Tree in Action (Traversal)

This article continues from Binary Tree Mindset (Overview), summarizing the general approach to solving binary tree problems:

This article uses several straightforward examples to demonstrate the application of these principles, helping you understand the differences and connections between the "traversal" and "problem decomposition" mindsets.

Problem 1: Invert Binary Tree

Let's begin with a simple problem, LeetCode problem 226: Invert Binary Tree. Given the root of a binary tree root, you are asked to invert the entire tree, for example, the input binary tree is as follows:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

The algorithm inverts the binary tree in-place, resulting in the tree with root as:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

It is evident that by swapping the left and right children of each node in the binary tree, you achieve the fully inverted binary tree.

Now, let's mentally recite the binary tree problem-solving guideline:

1. Can this problem be solved using the "traverse" approach?

Yes, I can write a traverse function to visit each node and swap its left and right children.

When focusing on a single node, what should it do? It should swap its left and right children.

When should this be done? It seems like it can be done in pre-order, in-order, or post-order position.

Based on the above, we can write the following solution code:

class Solution {
    // main function
    public TreeNode invertTree(TreeNode root) {
        // traverse the binary tree, swap the child nodes of each node
        traverse(root);
        return root;
    }

    // binary tree traversal function
    void traverse(TreeNode root) {
        if (root == null) {
            return;
        }

        // *** pre-order position ***
        // what each node needs to do is to swap its left and right children
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        // traversal framework, go traverse the nodes of the left and right subtrees
        traverse(root.left);
        traverse(root.right);
    }
}

class Solution {
public:
    // main function
    TreeNode* invertTree(TreeNode* root) {
        // traverse the binary tree, swap the child nodes of each node
        if(root != NULL) traverse(root);
        return root;
    }

    // binary tree traversal function
    void traverse(TreeNode* root) {
        if(root != NULL) {
            // *** pre-order position ***
            // what each node needs to do is to swap its left and right child nodes
            TreeNode* tmp = root->left;
            root->left = root->right;
            root->right = tmp;

            // traversal framework, go and traverse the nodes of the left and right subtrees
            traverse(root->left);
            traverse(root->right);
        }
    }
};

class Solution:
    # main function
    def invertTree(self, root):
        # traverse the binary tree, swap the children of each node
        self.traverse(root)
        return root

    # binary tree traversal function
    def traverse(self, root):
        if not root:
            return 
        
        # *** pre-order position ***
        # what each node needs to do is swap its left and right children
        tmp = root.left
        root.left = root.right
        root.right = tmp

        # traversal framework, go traverse the nodes of the left and right subtrees
        self.traverse(root.left)
        self.traverse(root.right)

// main function
func invertTree(root *TreeNode) *TreeNode {
    // traverse the binary tree, swap the child nodes of each node
    traverse(root)
    return root
}

// binary tree traversal function
func traverse(root *TreeNode) {
    if root == nil {
        return
    }

    // *** preorder position ***
    // what each node needs to do is swap its left and right children
    tmp := root.Left
    root.Left = root.Right
    root.Right = tmp

    // traversal framework, go and traverse the nodes of the left and right subtrees
    traverse(root.Left)
    traverse(root.Right)
}

// main function
var invertTree = function(root) {
    traverse(root);
    return root;
};

// binary tree traversal function
function traverse(root) {
    if (root == null) {
        return;
    }

    // *** preorder position ***
    // what each node needs to do is swap its left and right children
    let tmp = root.left;
    root.left = root.right;
    root.right = tmp;

    // traversal framework, go and traverse the nodes of the left and right subtrees
    traverse(root.left);
    traverse(root.right);
}

You can move the code from the pre-order position to the post-order position, but directly moving it to the in-order position won't work; it needs a slight modification. This should be quite obvious, so I won't elaborate on it.

Technically, we've solved this problem, but for comparison, let's continue thinking.

2. Can this problem be solved using the "divide and conquer" approach?

Let's try to define the invertTree function:

// definition: invert the binary tree with root, and
// return the root node of the inverted binary tree
TreeNode invertTree(TreeNode root);

// definition: invert the binary tree with root,
// return the root node of the inverted binary tree
TreeNode* invertTree(TreeNode* root);

# Definition: Invert the binary tree rooted at 'root', return the root node of the inverted tree
def invertTree(root: TreeNode)

// Definition: Invert the binary tree rooted at
// 'root', return the root node of the inverted tree
func invertTree(root *TreeNode) *TreeNode

// Definition: Invert the binary tree rooted at
// 'root', return the root node of the inverted tree
var invertTree = function(root) {}

Then think about it, when you execute invertTree(x) for a certain binary tree node x, what can you do using the definition of this recursive function?

I can use invertTree(x.left) to first invert the left subtree of x, then use invertTree(x.right) to invert the right subtree of x. Finally, I swap the left and right subtrees of x. This exactly completes the inversion of the entire binary tree rooted at x, thus fulfilling the definition of invertTree(x).

Here is the solution code directly:

class Solution {
    // Definition: Invert the binary tree rooted at
    // 'root', return the root node of the inverted
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        // Utilize the function definition to invert left and right subtrees first
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);

        // Then swap the left and right child nodes
        root.left = right;
        root.right = left;

        // Consistent with the definition logic: the
        // binary tree rooted at 'root' has been inverted,
        return root;
    }
}

class Solution {
public:
    // Definition: Invert the binary tree rooted at
    // 'root', return the root node of the inverted
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        // Utilize the function definition to invert the left and right subtrees first
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);

        // Then swap the left and right child nodes
        root->left = right;
        root->right = left;

        // Consistent with the definition logic: the
        // binary tree rooted at 'root' has been inverted,
        return root;
    }
};

class Solution:
    # Definition: Invert the binary tree rooted at
    # 'root', return the root node of the inverted
    def invertTree(self, root):
        if root is None:
            return None
        # Utilize the function definition to invert left and right subtrees first
        left = self.invertTree(root.left)
        right = self.invertTree(root.right)

        # Then swap the left and right child nodes
        root.left, root.right = right, left

        # Consistent with the definition logic: the
        # tree rooted at 'root' has been inverted,
        return root

// Definition: Invert the binary tree rooted at
// 'root', return the root node of the inverted tree
func invertTree(root *TreeNode) *TreeNode {
    if root == nil {
        return nil
    }
    // Use the function definition to invert the left and right subtrees first
    left := invertTree(root.Left)
    right := invertTree(root.Right)

    // Then swap the left and right child nodes
    root.Left = right
    root.Right = left

    // Consistent with the definition logic: the binary
    // tree rooted at 'root' has been inverted, return
    return root
}

// Definition: Invert the binary tree rooted at
// 'root', and return the root node of the inverted
var invertTree = function(root) {
    if (root == null) {
        return null;
    }
    // Utilize the function definition to invert left and right subtrees first
    var left = invertTree(root.left);
    var right = invertTree(root.right);

    // Then swap the left and right child nodes
    root.left = right;
    root.right = left;

    // Consistent with the definition logic: the binary
    // tree rooted at 'root' has been inverted, return
    return root;
}

The core of this "problem decomposition" approach is to give the recursive function a suitable definition, then use this definition to interpret your code. If your logic is self-consistent, it indicates that your algorithm is correct.

Alright, let's conclude the analysis of this problem. Both "traversal" and "problem decomposition" approaches can solve it. Let's look at the next problem.

Problem Two: Populate Right Pointers in Nodes

This is LeetCode problem 116, "Populating Next Right Pointers in Each Node". Let's examine the problem:

116. Populating Next Right Pointers in Each Node | LeetCode |  🟠

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

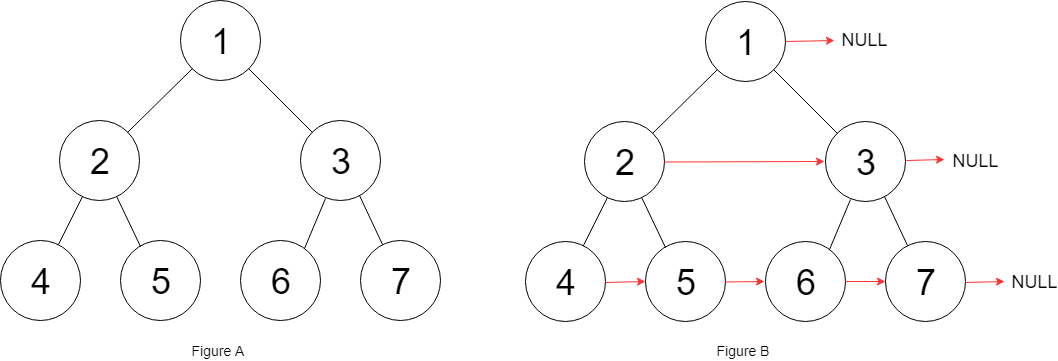
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 212 - 1].
• -1000 <= Node.val <= 1000

Follow-up:

• You may only use constant extra space.
• The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

The problem is from LeetCode 116. Populating Next Right Pointers in Each Node.

// Function signature
Node connect(Node root);

// Function signature
Node* connect(Node* root);

# Function signature
def connect(root: 'Node')

// Function signature
func connect(root *Node) *Node

// Function signature
var connect = function(root) {}

The problem is to connect all nodes at each level of a binary tree using the next pointer:

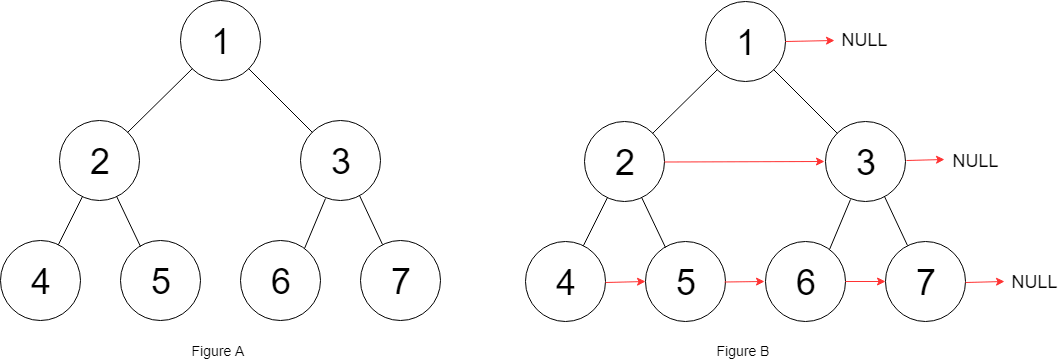
Moreover, the problem states that the input is a "perfect binary tree," meaning the entire binary tree forms an equilateral triangle. Except for the rightmost nodes, whose next pointers will point to null, all other nodes have adjacent nodes to their right.

How do we solve this problem? Let's mentally go through the binary tree problem-solving approach:

1. Can this problem be solved with a "traversal" mindset?

Certainly, it can.

Each node's task is straightforward: simply set its next pointer to point to the node on its right.

You might be tempted to mimic the previous problem and write code like this:

// Binary tree traversal function
void traverse(Node root) {
    if (root == null || root.left == null) {
        return;
    }
    // Point the next pointer of the left child to the right child
    root.left.next = root.right;

    traverse(root.left);
    traverse(root.right);
}

// Binary tree traversal function
void traverse(TreeNode* root) {
    if (root == NULL || root->left == NULL) {
        return;
    }
    // Point the next pointer of the left child to the right child
    root->left->next = root->right;

    traverse(root->left);
    traverse(root->right);
}

# Binary tree traversal function
def traverse(root):
    if root is None or root.left is None:
        return
    # Point the next pointer of the left child to the right child
    root.left.next = root.right

    traverse(root.left)
    traverse(root.right)

// Binary tree traversal function
func traverse(root *Node) {
    if root == nil || root.Left == nil {
        return
    }
    // Point the Next pointer of the left child to the right child
    root.Left.Next = root.Right

    traverse(root.Left)
    traverse(root.Right)
}

// Binary tree traversal function
var traverse = function(root) {
    if (root == null || root.left == null) {
        return;
    }
    // Point the next pointer of the left child to the right child
    root.left.next = root.right;

    traverse(root.left);
    traverse(root.right);
}

However, this code has significant issues because it can only connect two nodes with the same parent node. Take a look at this diagram:

Node 5 and Node 6 do not share the same parent node, so according to this code's logic, they cannot be linked, which does not meet the intended requirements. So, where does the problem lie?

The traditional traverse function is designed to visit all nodes of a binary tree, but what we actually want to traverse are the "gaps" between two adjacent nodes.

Therefore, we can abstract the binary tree by considering each box in the diagram as a node:

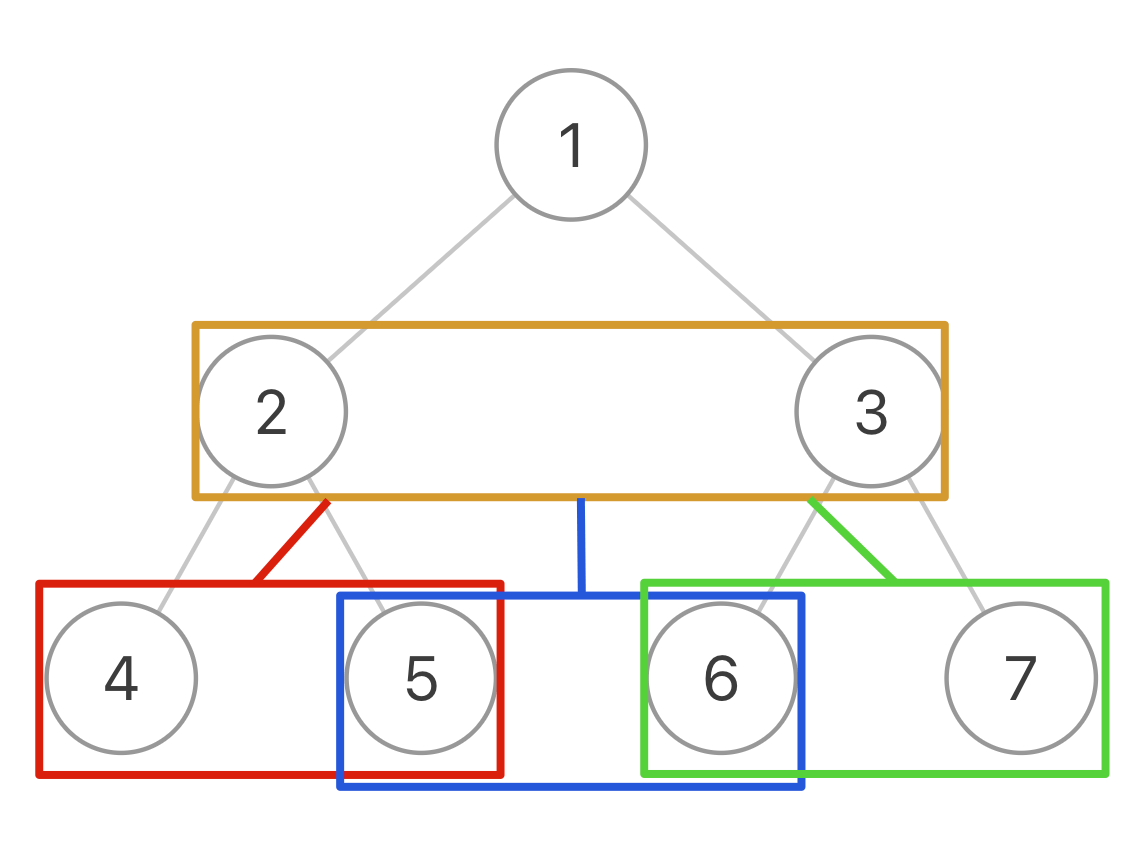
In this way, a binary tree is abstracted into a ternary tree, where each node on the ternary tree represents two adjacent nodes of the original binary tree.

Now, we just need to implement a traverse function to traverse this ternary tree. The task for each "ternary tree node" is to connect its two internal binary tree nodes.

class Solution {
    // Main function
    public Node connect(Node root) {
        if (root == null) return null;
        // Traverse the "ternary tree" and connect adjacent nodes
        traverse(root.left, root.right);
        return root;
    }

    // Ternary tree traversal framework
    void traverse(Node node1, Node node2) {
        if (node1 == null || node2 == null) {
            return;
        }
        // *** Pre-order position ***
        // Connect the two input nodes
        node1.next = node2;
        
        // Connect two child nodes with the same parent
        traverse(node1.left, node1.right);
        traverse(node2.left, node2.right);
        // Connect two child nodes across parent nodes
        traverse(node1.right, node2.left);
    }
}

class Solution {
public:
    // Main function
    Node* connect(Node* root) {
        if (root == nullptr) return nullptr;
        // Traverse the "ternary tree" and connect adjacent nodes
        traverse(root->left, root->right);
        return root;
    }

    // Ternary tree traversal framework
    void traverse(Node* node1, Node* node2) {
        if (node1 == nullptr || node2 == nullptr) {
            return;
        }
        // *** Pre-order position ***
        // Connect the two input nodes
        node1->next = node2;
        
        // Connect two child nodes with the same parent
        traverse(node1->left, node1->right);
        traverse(node2->left, node2->right);
        // Connect two child nodes across different parents
        traverse(node1->right, node2->left);
    }
};

class Solution:
    # Main function
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return None
        # Traverse the "ternary tree" and connect adjacent nodes
        self.traverse(root.left, root.right)
        return root

    # Ternary tree traversal frameworkf'd
    def traverse(self, node1: 'Node', node2: 'Node') -> None:
        if not node1 or not node2:
            return
        # Pre-order position
        # Connect the two input nodes
        node1.next = node2 
        
        # Connect two child nodes with the same parent
        self.traverse(node1.left, node1.right)
        self.traverse(node2.left, node2.right)
        # Connect two child nodes across different parents
        self.traverse(node1.right, node2.left)

// Main function
func connect(root *Node) *Node {
    if root == nil {
        return nil
    }
    // Traverse the "ternary tree" and connect adjacent nodes
    traverse(root.Left, root.Right)
    return root
}

// Ternary tree traversal framework
func traverse(node1 *Node, node2 *Node) {
    if node1 == nil || node2 == nil {
        return
    }

    // *** Pre-order position ***
    // Connect the two input nodes
    node1.Next = node2
    
    // Connect two child nodes with the same parent
    traverse(node1.Left, node1.Right)
    traverse(node2.Left, node2.Right)
    // Connect two child nodes across different parents
    traverse(node1.Right, node2.Left)
}

var connect = function(root) {
    // main function
    if (root == null) return null;
    // traverse the "ternary tree" and connect adjacent nodes
    traverse(root.left, root.right);
    return root;

    // ternary tree traversal framework
    function traverse(node1, node2) {
        if (node1 == null || node2 == null) {
            return;
        }
        // *** pre-order position ***
        // connect the two input nodes
        node1.next = node2;
        
        // connect two child nodes of the same parent
        traverse(node1.left, node1.right);
        traverse(node2.left, node2.right);
        // connect two child nodes across different parents
        traverse(node1.right, node2.left);
    }
};

In this way, the traverse function traverses the entire "ternary tree" and connects all adjacent binary tree nodes, thereby avoiding the issues we encountered before and perfectly solving this problem.

2. Can this problem be solved using the "problem decomposition" approach?

Well, there doesn't seem to be any particularly good idea, so this problem cannot be solved using the "problem decomposition" approach.

Third Problem: Flatten Binary Tree to Linked List

This is LeetCode Problem 114 "Flatten Binary Tree to Linked List", let's take a look at the problem:

114. Flatten Binary Tree to Linked List | LeetCode |  🟠

Given the root of a binary tree, flatten the tree into a "linked list":

• The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
• The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

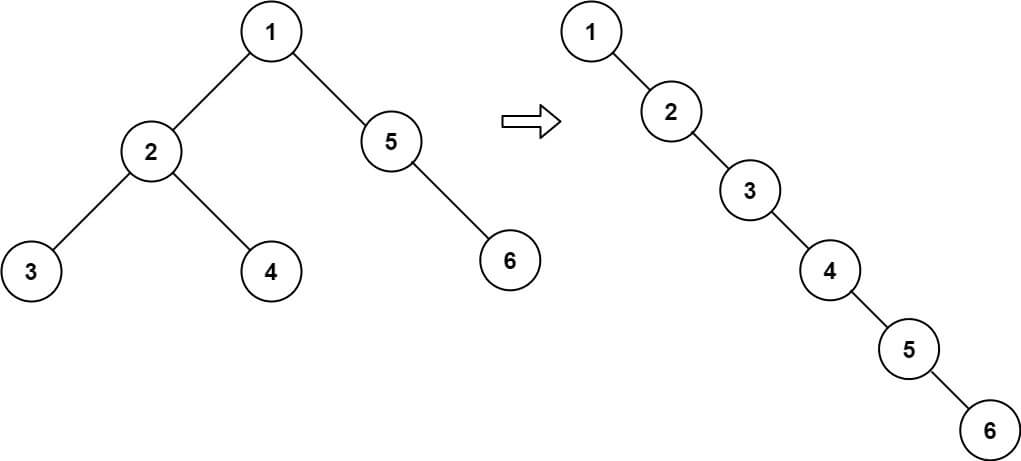
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -100 <= Node.val <= 100

Follow up: Can you flatten the tree in-place (with O(1) extra space)?

The problem is from LeetCode 114. Flatten Binary Tree to Linked List.

// The function signature is as follows
void flatten(TreeNode root);

// The function signature is as follows
void flatten(TreeNode* root);

# The function signature is as follows
def flatten(root: TreeNode)

// The function signature is as follows
func flatten(root *TreeNode)

// The function signature is as follows
var flatten = function(root) {}

1. Can this problem be solved with a "traversal" mindset?

At first glance, it seems possible: perform a pre-order traversal of the entire tree, constructing a "linked list" as you go:

// Virtual head node, dummy.right is the result
TreeNode dummy = new TreeNode(-1);
// Pointer used to build the linked list
TreeNode p = dummy;

void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // Pre-order position
    p.right = new TreeNode(root.val);
    p = p.right;

    traverse(root.left);
    traverse(root.right);
}

// Virtual head node, dummy.right is the result
TreeNode* dummy = new TreeNode(-1);
// Pointer used to build the linked list
TreeNode* p = dummy;

void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // Pre-order position
    p->right = new TreeNode(root->val);
    p = p->right;

    traverse(root->left);
    traverse(root->right);
}

# Virtual head node, dummy.right is the result
dummy = TreeNode(-1)
# Pointer used to build the linked list
p = dummy

def traverse(root: TreeNode):
    if root is None:
        return
    # Pre-order position
    p.right = TreeNode(root.val)
    p = p.right

    traverse(root.left)
    traverse(root.right)

var p *TreeNode

// Virtual head node, dummy.right is the result
var dummy = newTreeNode(-1)
p = dummy

func traverse(root *TreeNode) {
	if root == nil {
		return
	}
	// Pre-order position
	p.Right = &TreeNode{Val: root.Val}
	p = p.Right

	traverse(root.Left)
	traverse(root.Right)
}

// Virtual head node, dummy.right is the result
var dummy = new TreeNode(-1);
// Pointer used to build the linked list
var p = dummy;

var traverse = function(root) {
    if (root == null) {
        return;
    }
    // Pre-order position
    p.right = new TreeNode(root.val);
    p = p.right;

    traverse(root.left);
    traverse(root.right);
}

However, pay attention to the signature of the flatten function, which returns void. This means the problem expects us to flatten the binary tree into a linked list in place.

With this requirement, we cannot solve the problem through simple binary tree traversal.

2. Can this problem be solved using the "divide and conquer" thinking pattern?

Let's try to define the flatten function:

// Definition: Input node root, then the binary tree
// rooted at root will be flattened into a linked list
void flatten(TreeNode root);

// Definition: Input node root, then the binary tree
// rooted at root will be flattened into a linked list
void flatten(TreeNode* root);

# Definition: Input node root, then the binary tree with
# root as the root will be flattened into a linked list
def flatten(self, root: TreeNode) -> None:

// Definition: Input node root, then the binary tree with
// root as the root will be flattened into a linked list
func flatten(root *TreeNode) {
}

// Definition: Input node root, then the binary tree with
// root as the root will be flattened into a linked list
var flatten = function(root) {

};

With this function definition, how can we transform a tree into a linked list as required by the problem?

For a node x, you can follow these steps:

1. Use flatten(x.left) and flatten(x.right) to flatten the left and right subtrees of x.

2. Attach the right subtree of x below the left subtree, and then make the entire left subtree the right subtree.

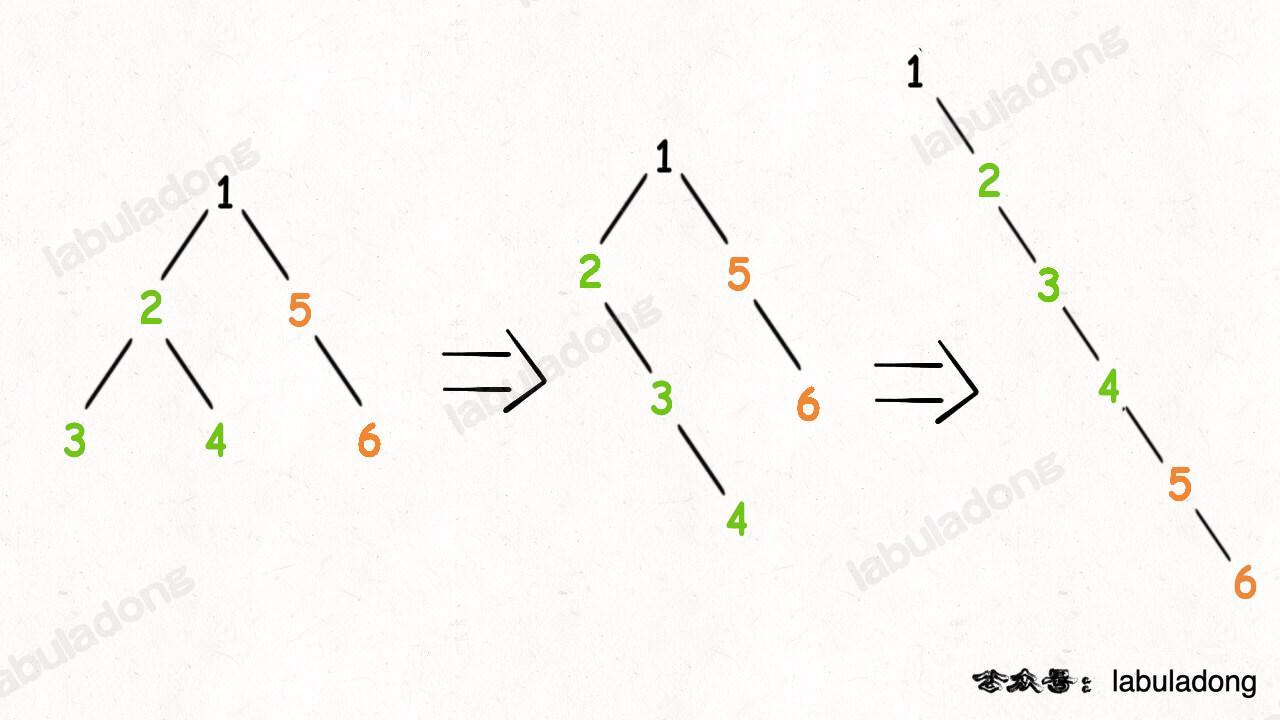
In this way, the entire binary tree rooted at x is flattened, effectively fulfilling the definition of flatten(x).

Let's look directly at the code implementation:

class Solution {
    // Definition: flatten the tree with root as the root node into a linked list
    public void flatten(TreeNode root) {
        // base case
        if (root == null) return;
        
        // Utilize the definition to flatten the left and right subtrees
        flatten(root.left);
        flatten(root.right);

        // *** Post-order traversal position ***
        // 1. Left and right subtrees have been flattened into linked lists
        TreeNode left = root.left;
        TreeNode right = root.right;
        
        // 2. Make the left subtree the new right subtree
        root.left = null;
        root.right = left;

        // 3. Attach the original right subtree to the end of the current right subtree
        TreeNode p = root;
        while (p.right != null) {
            p = p.right;
        }
        p.right = right;

    }
}

class Solution {
public:
    // Definition: flatten the tree rooted at 'root' into a linked list
    void flatten(TreeNode* root) {
        // base case
        if (root == nullptr) return;

        // Use the definition to flatten the left and right subtrees
        flatten(root->left);
        flatten(root->right);

        // *** Post-order traversal position ***
        // 1. Left and right subtrees have been flattened into linked lists
        TreeNode* left = root->left;
        TreeNode* right = root->right;

        // 2. Make the left subtree the new right subtree
        root->left = nullptr;
        root->right = left;

        // 3. Attach the original right subtree to the end of the current right subtree
        TreeNode* p = root;
        while (p->right != nullptr) {
            p = p->right;
        }
        p->right = right;

    }
};

class Solution:
    # Definition: flatten the tree rooted at 'root' into a linked list
    def flatten(self, root) -> None:
        # base case
        if root is None:
            return

        # Use the definition to flatten left and right subtrees
        self.flatten(root.left)
        self.flatten(root.right)

        # Post-order traversal position
        # 1. Left and right subtrees have been flattened into linked lists
        left = root.left
        right = root.right

        # 2. Make the left subtree the new right subtree
        root.left = None
        root.right = left

        # 3. Attach the original right subtree to the end of the current right subtree
        p = root
        while p.right is not None:
            p = p.right
        p.right = right 

// Definition: flatten the tree with root as the root into a linked list
func flatten(root *TreeNode) {
    // base case
    if root == nil {
        return
    }
    
    // Using the definition, flatten the left and right subtrees
    flatten(root.Left)
    flatten(root.Right)

    // *** Post-order traversal position ***
    // 1. Left and right subtrees have been flattened into a linked list
    left := root.Left
    right := root.Right
       
    // 2. Make the left subtree the right subtree
    root.Left = nil
    root.Right = left

    // 3. Attach the original right subtree to the end of the current right subtree
    p := root
    for p.Right != nil {
        p = p.Right
    }
    p.Right = right

}

var flatten = function(root) {
    // Definition: flatten the tree with root as the root into a linked list
    // base case
    if (root == null) return;

    // Utilize the definition to flatten the left and right subtrees
    flatten(root.left);
    flatten(root.right);

    // *** Post-order traversal position ***
    // 1. Left and right subtrees have been flattened into a linked list
    var left = root.left;
    var right = root.right;

    // 2. Make the left subtree the right subtree
    root.left = null;
    root.right = left;

    // 3. Attach the original right subtree to the end of the current right subtree
    var p = root;
    while (p.right != null) {
        p = p.right;
    }
    p.right = right;

};

See, this is the charm of recursion. You might wonder how the flatten function flattens the left and right subtrees.

It's not easy to explain, but as long as you understand the definition of flatten and use it, allowing each node to perform its task, the flatten function will work according to its definition.

With this, the problem is solved. The recursive approach from our previous discussion on Reverse Nodes in k-Group is somewhat similar to this problem.

Finally, let's revisit the fundamental solution framework for binary tree problems.

There are two main thinking patterns for solving binary tree problems:

1. Can you solve the problem by traversing the binary tree once? If so, use a traverse function along with external variables. This is known as the "traversal" thinking pattern.

2. Can you define a recursive function that derives the solution to the main problem from the solutions to subproblems (subtrees)? If so, write the definition of this recursive function and make full use of its return value. This is known as the "problem decomposition" thinking pattern.

No matter which thinking pattern you use, consider this:

If you isolate a single binary tree node, what task does it need to perform? At which order position (pre-order/in-order/post-order) should it be performed? You don't need to worry about the other nodes; the recursive function will execute the same operation on all nodes.

I hope you reflect on this approach and apply it to all binary tree problems.

This concludes the article. For more classic binary tree exercises and training in recursive thinking, please refer to the Recursion Practice section in the binary tree chapter.