Basic Concept of Union Find Algorithm

This article will introduce the concept of the dynamic connectivity problem in graphs and explain why the Union Find algorithm is an efficient solution for this problem.

We will use a visualization panel to intuitively demonstrate the core principles of the Union Find algorithm and the effects of several optimization strategies.

As this is a foundational chapter, we will not delve into the implementation details of the algorithm code. The specific code implementation and application in algorithm problems will be covered in later sections: Union Find Algorithm Implementation and Application and Classic Union Find Exercises. It is recommended for beginners to follow the sequence in the directory for a step-by-step learning process.

Dynamic Connectivity and Terminology

Graph theory algorithms come with numerous technical terms. Let's introduce a few of these terms using a simple example.

Consider the following example with 10 nodes labeled from 0 to 9. Even though there are no edges, it still constitutes a graph structure:

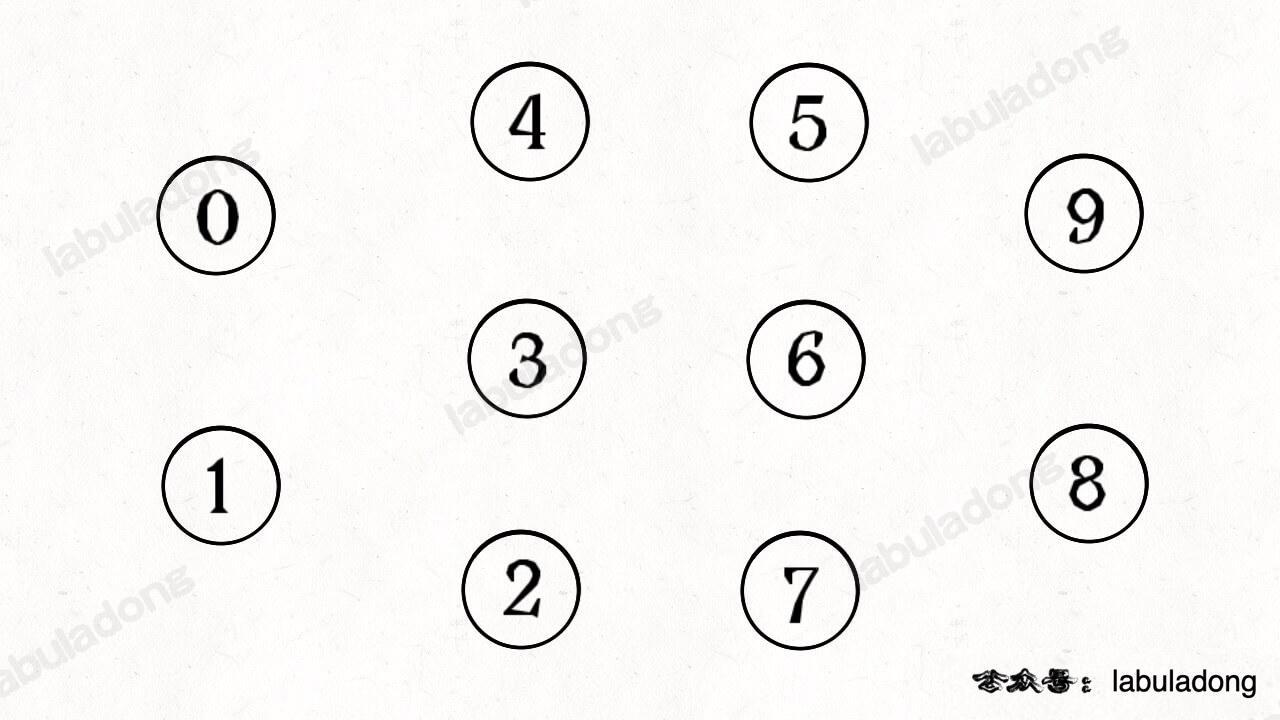
In this graph structure, we can say there are 10 "connected components," with each node being its own connected component since they are not connected to any other node.

Now, let's perform some "union operations" on these nodes, such as connecting nodes 0,1 and 1,2:

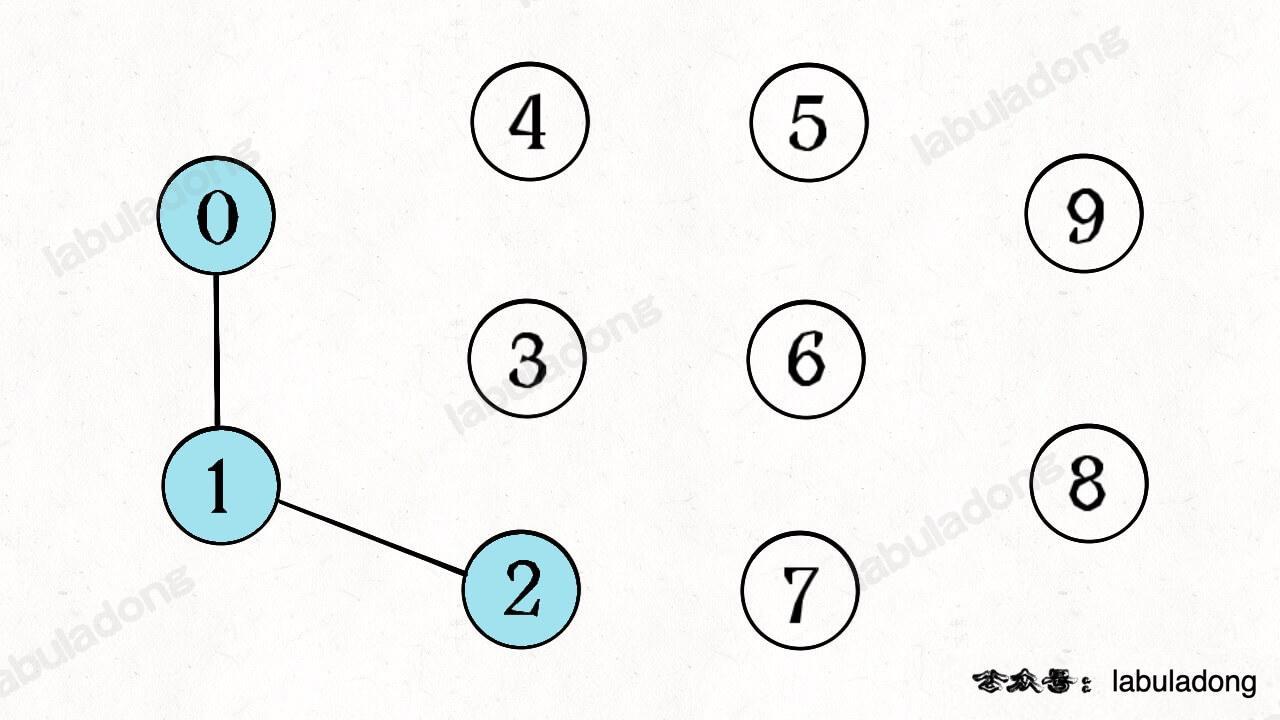
At this point, nodes 0, 1, 2 in the graph structure are connected, together forming a single connected component. We can say these three nodes are "connected."

Simultaneously, the number of connected components in this graph structure has decreased from 10 to 8, because the union operation merged the three connected components 0, 1, 2 into one.

The dynamic connectivity problem involves giving you a graph structure, performing several "union operations," and possibly querying whether any two nodes are "connected," or how many "connected components" currently exist in the graph.

Our goal is to design a data structure that performs union and query operations with minimal time complexity.

Why We Need the Union-Find Algorithm

The Union-Find structure provides the following API:

class UF {
    // Initialize Union Find with n nodes, time complexity O(n)
    public UF(int n);

    // Connect node p and node q, time complexity O(1)
    public void union(int p, int q);

    // Check if node p and node q are connected (in
    // the same connected component), time complexity
    public boolean connected(int p, int q);

    // Get the total number of connected components, time complexity O(1)
    public int count();
}

The union method is used to connect two nodes, the connected method is for checking if two nodes are connected, and the count method is for querying the number of connected components in the current graph. All these operations can be completed in $O(1)$ time.

The time complexity of $O(1)$ is the most efficient. If you haven't learned the union-find algorithm, how would you implement these methods?

There are some ways, for instance, the Graph Structure Basics and General Code Implementation section introduces the adjacency list/matrix implementation of graph structures. The union method is essentially adding an undirected edge to the graph, which can also be achieved in $O(1)$ time complexity.

How to implement the connected method? Are you thinking of checking the adjacency list/matrix to see if these two nodes are connected?

That's incorrect. Do not forget the "transitive" property mentioned above: if node p is connected to q, and q is connected to r, then p is also connected to r.

Simply checking the adjacency list/matrix only determines if two nodes are directly connected, and cannot handle this transitive connection.

Therefore, to implement connected(a, b), we must use the DFS/BFS Traversal Algorithm for graph structures. Start from node a and traverse all reachable nodes to see if node b is among them, thereby determining whether nodes a and b are connected.

In this case, the worst time complexity for the connected method is the complexity of graph traversal, which is $O(V+E)$, where $V$ is the number of nodes and $E$ is the number of edges.

Next, how to implement the count method?

Again, it relies on the DFS/BFS Traversal Algorithm for graph structures, but it's more complicated.

You need to use BFS/DFS to traverse the entire graph, classify all nodes into different connected components, and finally count the number of connected components. This process has a time complexity of $O(V+E)$.

Therefore, the union-find algorithm is very ingenious. It not only completes the above operations in $O(1)$ time but also does not need to construct a graph structure using an adjacency list/matrix, only an array is needed.

The detailed explanation follows.