Queue/Stack Basic

The two storage methods in computers, sequential storage (arrays) and linked storage (linked lists), have been covered. All subsequent data structures are based on these two storage methods.

This article explains the basic principles of queues and stacks, with future articles detailing how to implement them in code.

To start with the concepts, both queues and stacks are "restricted operation" data structures. Compared to basic arrays and linked lists, their APIs are not complete.

For example, with the arrays and linked lists we implemented earlier, you can perform CRUD operations on any indexed element as long as the index is within bounds.

However, the operations for queues and stacks are restricted: A queue allows insertion at one end and removal from the other; a stack allows insertion and removal only at one end. Essentially, some of the APIs provided by arrays and linked lists are removed, leaving only the APIs for manipulating elements at the ends.

To understand visually, a queue only allows inserting elements at the back and removing elements from the front, while a stack only allows inserting and removing elements at the top. The illustration shows the stack drawn vertically and the queue horizontally for better visualization, but they are both implemented using arrays and linked lists, which will be discussed later:

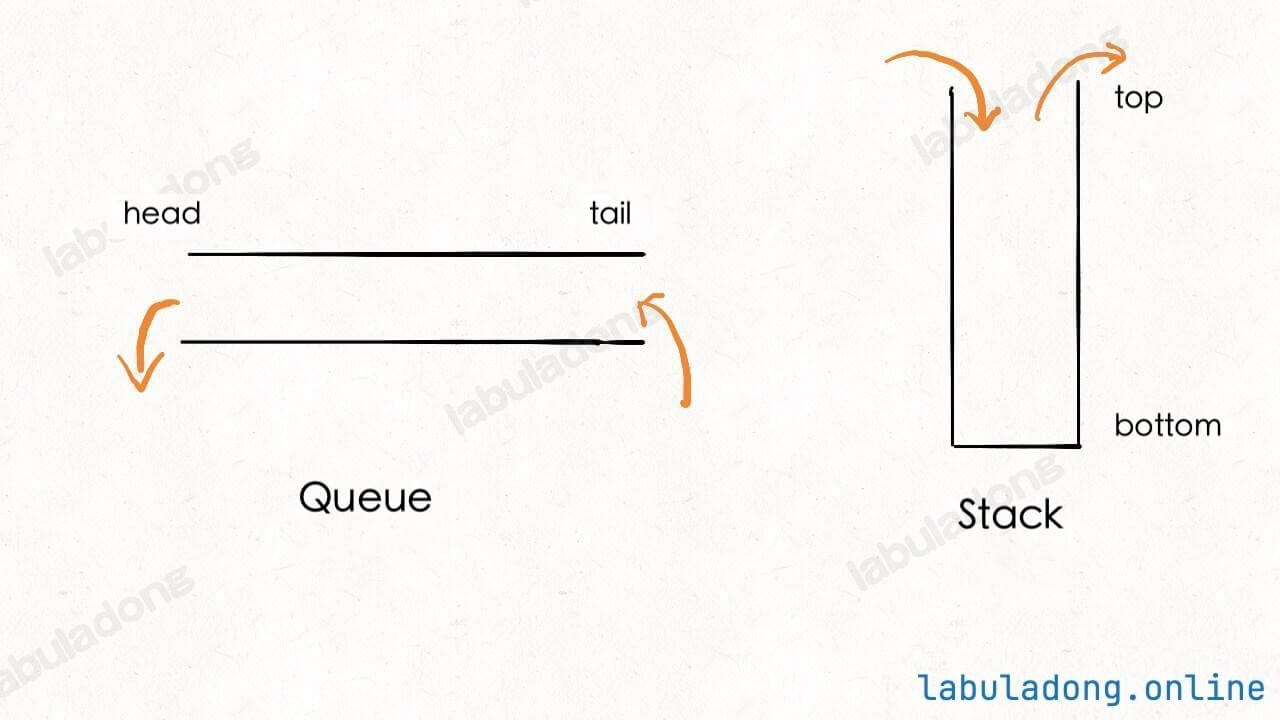
A queue is like buying tickets in line, where the first to arrive is the first to leave, and the last to arrive is the last to leave; a stack is like a stack of plates, with the first placed at the bottom and the last placed at the top, and the topmost is the first to be removed. Therefore, we often say that a queue is a "first-in, first-out" data structure, while a stack is a "first-in, last-out" data structure.

The basic APIs for these two data structures are as follows:

// Basic API of the queue
class MyQueue<E> {
    // Insert an element at the end of the queue, time complexity O(1)
    void push(E e);

    // Remove an element from the front of the queue, time complexity O(1)
    E pop();

    // View the element at the front of the queue, time complexity O(1)
    E peek();

    // Return the number of elements in the queue, time complexity O(1)
    int size();
}

// Basic API of the stack
class MyStack<E> {
    // Insert an element at the top of the stack, time complexity O(1)
    void push(E e);

    // Remove an element from the top of the stack, time complexity O(1)
    E pop();

    // View the element at the top of the stack, time complexity O(1)
    E peek();

    // Return the number of elements in the stack, time complexity O(1)
    int size();
}

// Basic API of the queue
template <typename E>
class MyQueue {
public:
    // Insert an element at the end of the queue, time complexity O(1)
    void push(const E& e);

    // Remove an element from the front of the queue, time complexity O(1)
    E pop();

    // View the element at the front of the queue, time complexity O(1)
    E peek() const;

    // Return the number of elements in the queue, time complexity O(1)
    int size() const;
};

// Basic API of the stack
template <typename E>
class MyStack {
public:
    // Insert an element at the top of the stack, time complexity O(1)
    void push(const E& e);

    // Remove an element from the top of the stack, time complexity O(1)
    E pop();

    // View the element at the top of the stack, time complexity O(1)
    E peek() const;

    // Return the number of elements in the stack, time complexity O(1)
    int size() const;
};

# Basic API of the queue
class MyQueue:

    # Insert an element at the end of the queue, time complexity O(1)
    def push(self, e):
        pass

    # Delete an element from the front of the queue, time complexity O(1)
    def pop(self):
        pass

    # View the element at the front of the queue, time complexity O(1)
    def peek(self):
        pass

    # Return the number of elements in the queue, time complexity O(1)
    def size(self):
        pass

# Basic API of the stack
class MyStack:
    
    # Insert an element at the top of the stack, time complexity O(1)
    def push(self, e):
        pass
    
    # Delete an element from the top of the stack, time complexity O(1)
    def pop(self):
        pass
    
    # View the element at the top of the stack, time complexity O(1)
    def peek(self):
        pass
    
    # Return the number of elements in the stack, time complexity O(1)
    def size(self):
        pass

// Basic API of the queue
type MyQueue[T any] struct {
}

// Insert element at the end of the queue, time complexity O(1)
func (q *MyQueue[T]) Push(e T) {}

// Delete element from the front of the queue, time complexity O(1)
func (q *MyQueue[T]) Pop() T {}

// View the element at the front of the queue, time complexity O(1)
func (q *MyQueue[T]) Peek() T {}

// Return the number of elements in the queue, time complexity O(1)
func (q *MyQueue[T]) Size() int {}

// Basic API of the stack
type MyStack[T any] struct {
}

// Insert element at the top of the stack, time complexity O(1)
func (s *MyStack[T]) Push(e T) {}

// Delete element from the top of the stack, time complexity O(1)
func (s *MyStack[T]) Pop() T {}

// View the element at the top of the stack, time complexity O(1)
func (s *MyStack[T]) Peek() T {}

// Return the number of elements in the stack, time complexity O(1)
func (s *MyStack[T]) Size() int {}

// Basic API of the queue
class MyQueue {
    // Insert element at the end of the queue, time complexity O(1)
    push(e) {}

    // Delete element from the front of the queue, time complexity O(1)
    pop() {}

    // View the element at the front of the queue, time complexity O(1)
    peek() {}

    // Return the number of elements in the queue, time complexity O(1)
    size() {}
}

class MyStack {
    // Insert element at the top of the stack, time complexity O(1)
    push(e) {}

    // Delete element from the top of the stack, time complexity O(1)
    pop() {}

    // View the element at the top of the stack, time complexity O(1)
    peek() {}

    // Return the number of elements in the stack, time complexity O(1)
    size() {}
}

Different programming languages may have different method names for queues and stacks, but the effect of each method is the same.

Some languages' standard libraries may not directly provide queues and stacks, but you can simulate the behavior of queues and stacks using arrays or linked lists. In the next chapter, I will first guide you in implementing queues and stacks using linked lists.