Use Array to Enhance Hash Table (ArrayHashMap)

In the previous chapter Enhancing Hash Tables with Linked Lists, we used doubly linked lists to enhance hash tables, implementing a data structure like LinkedHashMap that maintains the insertion order of keys in a hash table.

Linked lists can enhance hash tables, and arrays, being good siblings to linked lists, can also enhance hash tables.

Adding randomKey() API

Now, here's a challenge for you: based on the standard hash table API, add a new randomKey() API that can return a random key in $O(1)$ time complexity:

interface Map<K, V> {
    // Get the value corresponding to the key, time complexity O(1)
    V get(K key);

    // Add/modify key-value pair, time complexity O(1)
    void put(K key, V value);

    // Remove key-value pair, time complexity O(1)
    void remove(K key);

    // Check if the key is contained, time complexity O(1)
    boolean containsKey(K key);

    // Return all keys, time complexity O(N)
    List<K> keys();

    // New API: Randomly return a key, required time complexity O(1)
    K randomKey();
}

So, can you solve this? Don't underestimate this simple requirement. The way to do it is actually clever.

From what you learned before, you know that a hash table is basically a table array. Now, if you want to randomly return a key from a hash table, it's easy to think of picking a random element from the array.

For a normal array, picking a random element is simple. Just use a random number generator to get a random index in [0, size), and you get a random element:

int randomeElement(int[] arr) {
    Random r = new Random();
    // generate a random index in the range [0, arr.length)
    return arr[r.nextInt(arr.length)];
}

int randomeElement(vector<int>& arr) {
    // generate a random index in the range [0, arr.size())
    return arr[rand() % arr.size()];
}

import random

def randomeElement(arr: List[int]) -> int:
    # generate a random index in the range [0, len(arr))
    return arr[random.randint(0, len(arr) - 1)]

import "math/rand"

func randomeElement(arr []int) int {
    // generate a random index in the range [0, len(arr))
    return arr[rand.Intn(len(arr))]
}

function randomeElement(arr) {
    // generate a random index in the range [0, arr.length)
    return arr[Math.floor(Math.random() * arr.length)];
}

This algorithm is correct. Its time complexity is O(1), and each element is picked with probability 1/n, where n is the length of the arr array.

But notice, this function assumes that the array is compact, with no empty spots. For example, arr = [1, 2, 3, 4]. This way, every random index points to a valid element.

If the array has empty spots, things get tricky. For example, arr = [1, 2, null, 4], where arr[2] = null means there's no element in spot 2. If your random number happens to be 2, what should you do?

Maybe you would say, just search left or right to find the next non-empty element and return it, like this:

// return a non-null random element (pseudo code)
int randomeElement(int[] arr) {
    Random r = new Random();
    // generate a random index in the range [0, arr.length)
    int i = r.nextInt(arr.length);
    while (arr[i] == null) {
        // the randomly generated index i happens to be null
        // use the circular array technique to probe to the right
        // until a non-null element is found
        i = (i + 1) % arr.length;
    }
    return arr[i];
}

This approach is not feasible, as the algorithm has two issues:

1. There is a loop, causing the worst-case time complexity to rise to $O(N)$, which does not meet the $O(1)$ requirement.

2. The algorithm is not uniformly random, because your search direction is fixed, making the elements on the right side of the gap more likely to be selected. For example, for arr = [1, 2, null, 4], the probabilities of selecting elements 1, 2, 4 are 1/4, 1/4, 2/4, respectively.

There might be another way: if you have bad luck once, try randomizing several times until finding a non-null element:

// return a non-empty random element (pseudo code)
int randomeElement(int[] arr) {
    Random r = new Random();
    // generate a random index in the range [0, arr.length)
    int i = r.nextInt(arr.length);
    while (arr[i] == null) {
        // the randomly generated index i happens to be null
        // regenerate a random index
        i = r.nextInt(arr.length);
    }
    return arr[i];
}

Currently, this algorithm is uniformly random, but the issue is apparent: its time complexity unexpectedly depends on random numbers! It is definitely not $O(1)$, which doesn't meet the requirements.

Have you been stumped by the problem of randomly returning an element from an array with gaps?

Don't forget, our goal now is to randomly return a key from a hash table. The table array underlying the hash table not only contains gaps but is even more complex:

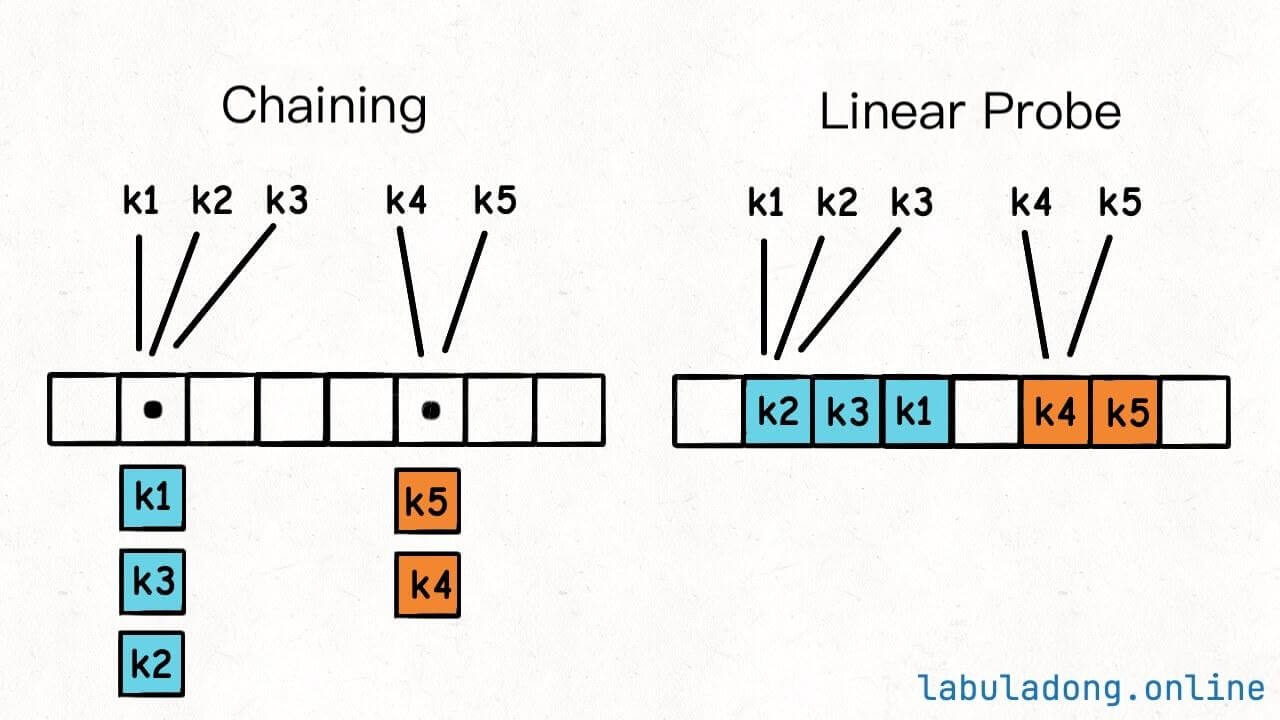
If your hash table uses open addressing to resolve hash collisions, then you're dealing with the scenario of an array with gaps.

If your hash table uses chaining, it's more complicated. Each element in the array is a linked list, so randomly selecting an index is not enough; you also need to randomly choose a node from the linked list.

Also, consider the probabilities. With chaining, even if you randomly choose an array index uniformly and then a node uniformly from the linked list at that index, is the key you get uniformly random?

Actually, it's not. In the image above, the probability of selecting k1, k2, k3 is 1/2 * 1/3 = 1/6, while the probability of selecting k4, k5 is 1/2 * 1/2 = 1/4, which is not uniformly random.

The only solution is to traverse the entire table array using the keys method, store all the keys in an array, and then randomly return one key. However, this results in a complexity of $O(N)$, which still doesn't meet the requirements.

Feeling stuck? This is why accumulating experience in designing classic data structures is essential. If you encounter similar issues during interviews or exams, it might be difficult to come up with a solution on the spot. Next, I will introduce how to enhance a hash table with arrays to easily implement the randomKey() API.

Implementation Idea

Code Implementation