Implement HashMap with Separate Chaining

In the previous article Core Principles of Hash Tables, I introduced the core principles and key concepts of hash tables. It mentioned that there are two main methods to resolve hash collisions: the chaining method and open addressing method (also known as linear probing):

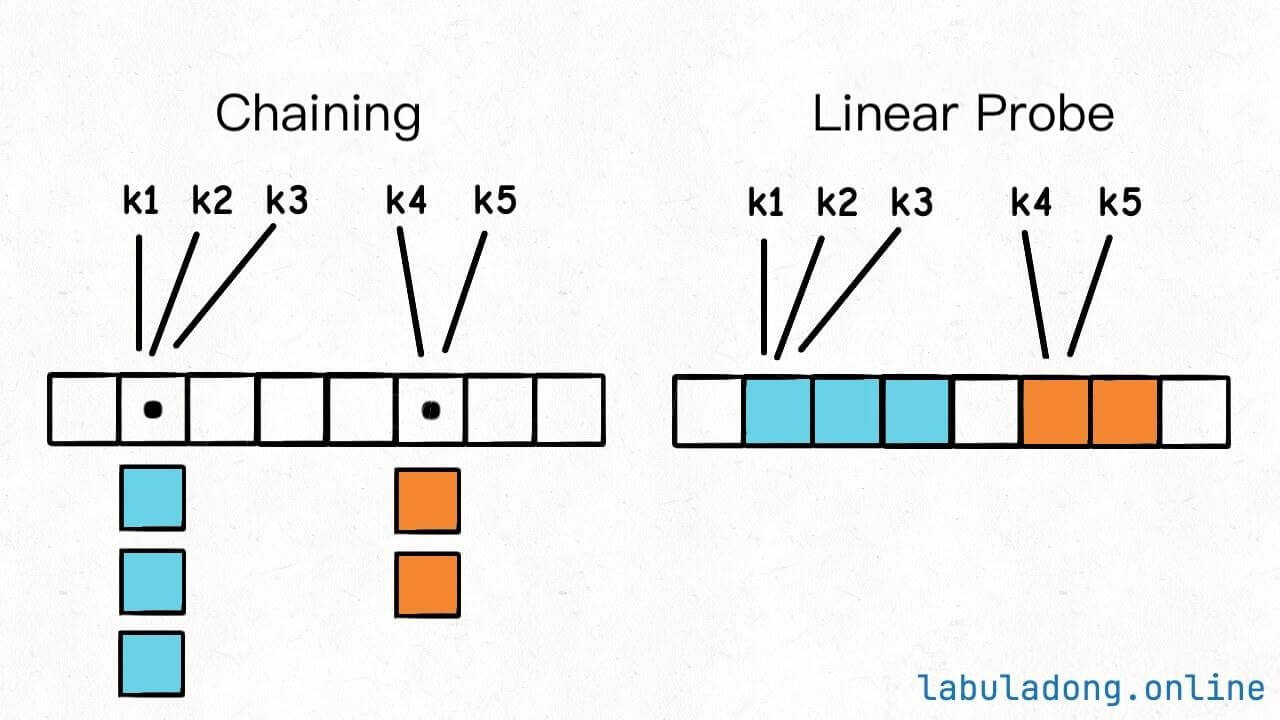
This article will specifically introduce the implementation principles and code for the chaining method.

Firstly, I will use a visualization panel to implement a simplified version of a hash table using the chaining method. This will help you intuitively understand how the chaining method implements the APIs for adding, deleting, finding, and updating, and how it resolves hash collisions. Finally, I will provide a more complete Java code implementation.

Simplified Implementation of the Chaining Method

The article Core Principles of Hash Tables has already explained the relationship between hash functions and the type of key. The role of a hash function is to convert a key into an index of an array in $O(1)$ time, and a key can be of any immutable type.

However, to facilitate understanding here, I will make the following simplifications:

1. The hash table we implement only supports key and value types as int. If the key does not exist, it returns -1.

2. The hash function we implement is simply a modulo operation, i.e., hash(key) = key % table.length. This also conveniently simulates hash collisions, for example, when table.length = 10, both hash(1) and hash(11) produce the value 1.

3. The size of the underlying table array is fixed upon the creation of the hash table, without considering load factors or dynamic resizing.

These simplifications help us focus on the core logic of adding, deleting, finding, and updating, and can be supported by the visualization panel to enhance understanding.