Basic Concept of HashMap

First, I need to clarify a common conceptual mistake made by beginners.

Are hash tables the same as what we commonly refer to as Maps (key-value mappings)? No.

This is clear when explained using Java. Map is a Java interface that only declares several methods without providing specific implementations:

interface Map<K, V> {
    V get(K key);
    void put(K key, V value);
    V remove(K key);
    // ...
}

The Map interface defines a series of key-value operations, while data structures like HashMap implement these operations based on their characteristics. Other data structures, like TreeMap and LinkedHashMap, also implement this interface.

In other words, you can say that the complexity of get, put, and remove methods for HashMap is $O(1)$, but you cannot claim that the complexity for the Map interface is $O(1)$. For other implementation classes like TreeMap, which uses a binary tree structure, these methods have a complexity of $O(logN)$.

Why do I emphasize this? Mainly for readers using non-Java languages.

Other programming languages may not have such clear interface definitions as Java, making it easy for readers to confuse hash tables with key-value pairs in Maps. They might assume that key-value operations must have a complexity of $O(1)$, which is incorrect. It depends on how the underlying data structure implements key-value operations.

In this section, I will guide you in implementing a hash table and discuss why hash tables can achieve $O(1)$ complexity for insertions, deletions, searches, and updates, as well as the two methods for resolving hash collisions.

Basic Principles of Hash Tables

A hash table can be understood as an enhanced version of an array.

An array can locate a corresponding element in $O(1)$ time complexity using an index, which is a non-negative integer.

A hash table is similar, allowing you to locate the value corresponding to a key in $O(1)$ time complexity. The key can be of various types, such as numbers or strings.

How is this done? It's quite simple. The underlying implementation of a hash table is an array (let's call it table). It converts the key into an index in the array using a hash function (let's call it hash), and then the operations of insertion, deletion, search, and update are similar to those of an array.

// Pseudocode logic for a hash table
class MyHashMap {

    private Object[] table;

    // Insert/Update, complexity O(1)
    public void put(K key, V value) {
        int index = hash(key);
        table[index] = value;
    }

    // Retrieve, complexity O(1)
    public V get(K key) {
        int index = hash(key);
        return table[index];
    }

    // Delete, complexity O(1)
    public void remove(K key) {
        int index = hash(key);
        table[index] = null;
    }

    // Hash function, converting key into a valid index in the table
    // The time complexity must be O(1) to ensure
    // that the above methods all have complexity
    private int hash(K key) {
        // ...
    }
}

// Pseudocode logic for hash table
class MyHashMap {

private:
    vector<void*> table;

public:
    // Insert/Update, complexity O(1)
    void put(auto key, auto value) {
        int index = hash(key);
        table[index] = value;
    }

    // Search, complexity O(1)
    auto get(auto key) {
        int index = hash(key);
        return table[index];
    }

    // Delete, complexity O(1)
    void remove(auto key) {
        int index = hash(key);
        table[index] = nullptr;
    }

private:
    // Hash function, convert key to valid index in the table
    // Time complexity must be O(1) to ensure the above methods have O(1) complexity
    int hash(auto key) {
        // ...
    }
};

# Hash table pseudocode logic
class MyHashMap:

    def __init__(self):
        self.table = [None] * 1000

    # add/update, complexity O(1)
    def put(self, key, value):
        index = self.hash(key)
        self.table[index] = value

    # get, complexity O(1)
    def get(self, key):
        index = self.hash(key)
        return self.table[index]

    # remove, complexity O(1)
    def remove(self, key):
        index = self.hash(key)
        self.table[index] = None

    # hash function, convert key into a valid index in the table
    # time complexity must be O(1) to ensure the above methods have O(1) complexity
    def hash(self, key):
        # ...
        pass

// Pseudo-code logic for hash table
type MyHashMap struct {
	table []interface{}
}

func Constructor() MyHashMap {
	return MyHashMap{
		table: make([]interface{}, 10000),
	}
}

// Add/Update, complexity O(1)
func (h *MyHashMap) Put(key, value interface{}) {
	index := h.hash(key)
	h.table[index] = value
}

// Get, complexity O(1)
func (h *MyHashMap) Get(key interface{}) interface{} {
	index := h.hash(key)
	return h.table[index]
}

// Remove, complexity O(1)
func (h *MyHashMap) Remove(key interface{}) {
	index := h.hash(key)
	h.table[index] = nil
}

// Hash function, convert key to a valid index in the table
// Time complexity must be O(1) to ensure the above methods are O(1)
func (h *MyHashMap) hash(key interface{}) int {
	...
}

// Hash table pseudocode logic
class MyHashMap {
    constructor() {
        this.table = new Array(1000).fill(null);
    }

    // Add/Update, complexity O(1)
    put(key, value) {
        const index = this.hash(key);
        this.table[index] = value;
    }

    // Get, complexity O(1)
    get(key) {
        const index = this.hash(key);
        return this.table[index];
    }

    // Remove, complexity O(1)
    remove(key) {
        const index = this.hash(key);
        this.table[index] = null;
    }

    // Hash function, convert key to a valid index in the table
    // The time complexity must be O(1) to ensure that the above methods' complexity are O(1)
    hash(key) {
        // ...
    }
}

There are many implementation details to handle, such as the design of hash functions and the handling of hash collisions. As long as you understand the core principles mentioned above, you are halfway there—writing the code is the remaining part, which shouldn't be difficult.

Let's delve into the key concepts and potential issues during the processes of addition, deletion, search, and update.

Key Concepts and Principles

key is Unique, value can be Duplicate

In a hash table, there cannot be two identical keys, but values can be repeated.

Understanding the principles mentioned above should make this clear. You can directly compare it to an array:

Each index in an array is unique; you cannot have two index 0s in an array. As for what elements are stored in the array, it's up to you—nobody cares.

Similarly, in a hash table, the key value cannot be duplicated, while the value can be anything you choose.

Hash Function

The purpose of a hash function is to convert inputs of arbitrary length (key) into fixed-length outputs (indices).

As seen, methods for addition, deletion, search, and update all use hash functions to calculate indices. If the hash function you design has a complexity of $O(N)$, the performance of additions, deletions, searches, and updates in the hash table will degrade to $O(N)$. Therefore, the performance of this function is crucial.

Another important aspect of this function is that it must ensure the same key input produces the same output, to maintain the correctness of the hash table. It cannot be that you calculate hash("123") = 5 now and hash("123") = 6 later, as this would render the hash table useless.

How does the hash function convert non-integer key types into integer indices? And how does it ensure these indices are valid?

int h = key.hashCode();
if (h < 0) h = -h;

int h = key.hashCode();
// Bitwise operation, remove the highest bit (sign bit)
// Additionally, bitwise operations are generally faster than arithmetic operations
// Therefore, you will see that the standard library
// source code prefers bitwise operations where possible
h = h & 0x7fffffff;
// The binary representation of 0x7fffffff is 0111 1111 ... 1111
// That is, all bits are 1 except the highest bit (sign bit) which is 0
// By performing a bitwise AND with 0x7fffffff, the highest
// bit (sign bit) is cleared, ensuring h is non-negative

int hash(K key) {
    int h = key.hashCode();
    // Ensure non-negative
    h = h & 0x7fffffff;
    // Map to a valid index in the table array
    return h % table.length;
}

Hash Collision

Above, we discussed the implementation of the hash function. Naturally, you might wonder, what happens if two different keys produce the same index through the hash function? This situation is known as a "hash collision."

How do we resolve hash collisions? There are two common solutions: chaining and linear probing (also often called open addressing).

The names might sound fancy, but they essentially boil down to two approaches: vertical extension and horizontal extension.

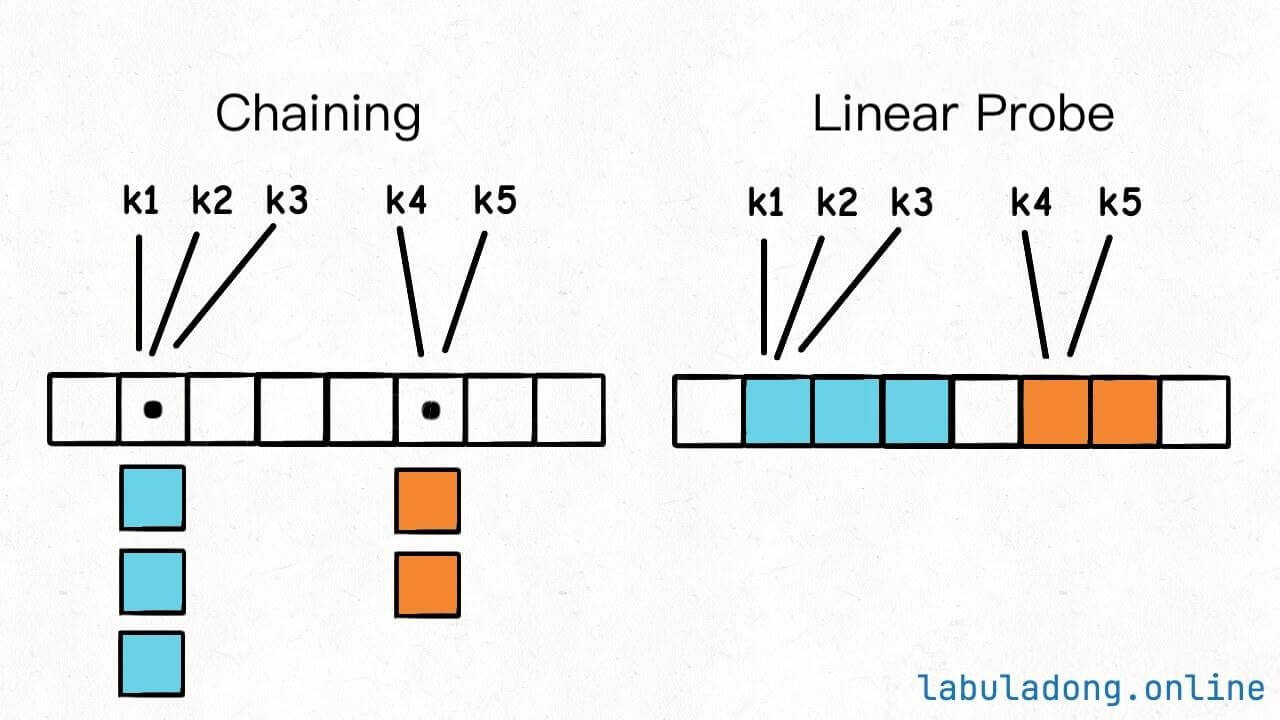
In chaining, the underlying array of the hash table doesn't store value types directly but stores a linked list. When multiple different keys map to the same index, these key -> value pairs are stored in the linked list, effectively resolving hash collisions.

In linear probing, if a key finds that the calculated index is already occupied by another key, it checks the position at index + 1. If that spot is also occupied, it continues to check subsequent positions until it finds an empty spot.

For example, in the image above, the keys are inserted in the order k2, k4, k5, k3, k1, resulting in the hash table looking like this:

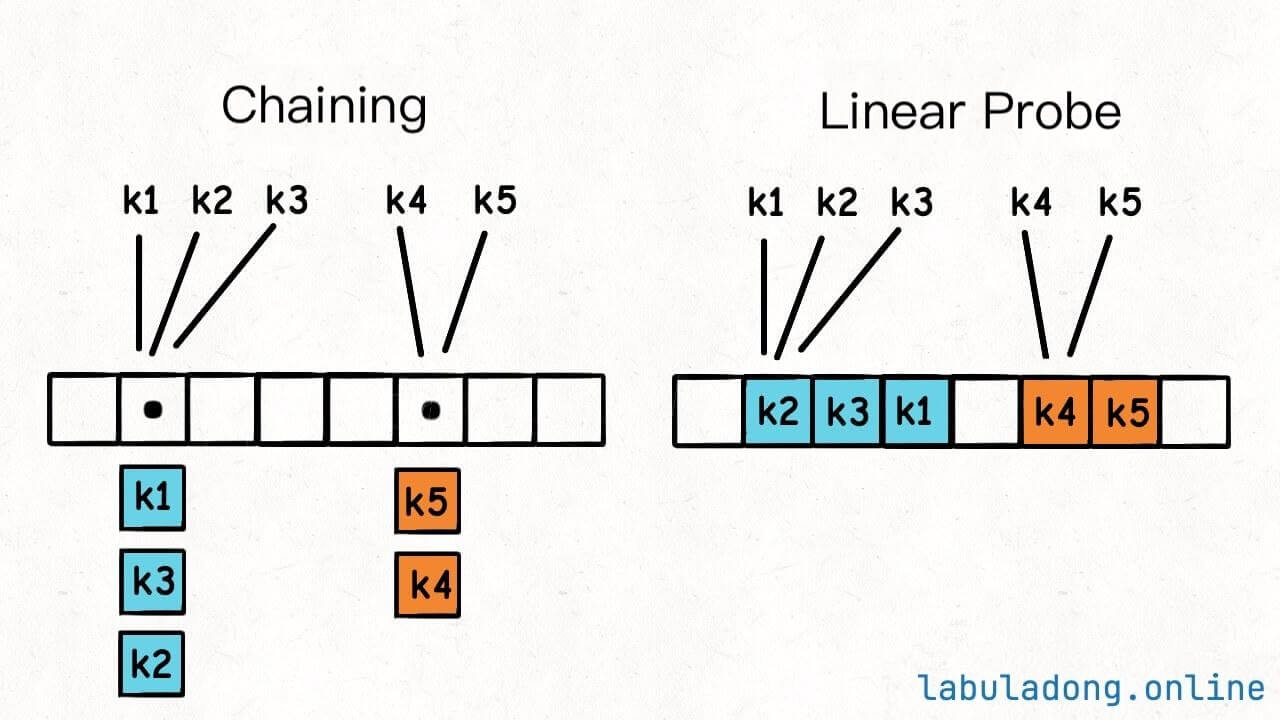
Here, I'll explain the principles first. In the following chapters, I will walk you through the implementation of these two methods to resolve hash collisions.

Capacity Expansion and Load Factor

You might have heard the term "load factor" before. Now that you understand the issue of hash collisions, you can grasp the significance of the load factor.

While chaining and linear probing methods can resolve hash collisions, they may lead to performance degradation.

For instance, with chaining, you calculate index = hash(key) and find a linked list at that index. You then need to traverse this list to locate the desired value. The time complexity of this process is $O(K)$, where K is the length of the linked list.

Linear probing is similar. You calculate index = hash(key) and check the index, but if the stored key isn't the one you are looking for, you can't be sure the key doesn't exist. You must keep searching until you find an empty spot or the key itself. This process also has a time complexity of $O(K)$, where K is the number of consecutive probes.

Therefore, frequent hash collisions increase the value of K, leading to a significant drop in hash table performance. This is something we aim to avoid.

Why do hash collisions occur frequently? There are two reasons:

1. A poorly designed hash function results in uneven distribution of key hash values, causing many keys to map to the same index.

2. The hash table is too full, making collisions inevitable even with a perfect hash function.

There's little to say about the first issue; language standard library developers have already designed the hash functions for you. You just need to use them.

The second issue is controllable — avoid overfilling the hash table, which introduces the concept of the "load factor."

Why You Shouldn't Rely on Hash Table Traversal Order

You may have heard the programming rule that the order of keys in a hash table is unordered, and you shouldn't rely on traversal order when writing programs. But why is that?

Hash table traversal essentially means traversing the underlying table array:

// pseudo-code logic for iterating all keys

// underlying table array of the hash table
KVNode[] table = new KVNode[1000];

// get all keys in the hash table
// we cannot rely on the order of this keys list
List<KeyType> keys = new ArrayList<>();

for (int i = 0; i < table.length; i++) {
    KVNode node = table[i];
    if (node != null) {
        keys.add(node.key);
    }
}

If you have understood the previous content, you should be able to comprehend this issue.

Firstly, since the hash function maps your key, the distribution of key in the underlying table array is random, unlike arrays or linked lists that have a clear order of elements.

Secondly, what happens when the hash table reaches the load factor? It expands, right? That means table.length changes, and elements are moved.

During this data moving process, doesn't the hash function need to recalculate the hash value of the key and place it in the new table array?

The hash function's computed value depends on table.length. Thus, after automatic expansion of the hash table, the hash value of the same key may change, meaning the storage index in table has also changed, so the order of traversal results differs from before.

The phenomenon you observe is that the first key in this traversal is key1, but after adding or deleting several elements and traversing again, you may find key1 has moved to the end.

Therefore, there's no need to memorize these things. Once you understand the principles, you can deduce the logic yourself.

Why It's Not Recommended to Add/Delete Hash Table Keys in a for Loop

Note that I say it's not recommended, not that it's impossible. Different programming languages have different implementations of hash tables in their standard libraries, and some have optimized for this situation. Whether it's feasible or not depends on consulting the documentation.

Analyzing only from the principle of hash tables, adding or deleting keys in a for loop can easily cause problems due to the same reason mentioned above—hash value changes caused by resizing.

Traversing hash table keys essentially means traversing the underlying table array. If you add or delete elements while traversing, and if an insert/delete operation triggers a resize halfway through, the entire table array changes. What behavior should follow? Also, should newly inserted/deleted elements during traversal be included in the traversal?

The order change of keys due to resizing is a unique behavior of hash tables. Even excluding this factor, any other data structure should not be modified during traversal to avoid unexpected behavior.

If you insist on doing so, ensure you have consulted the relevant documentation to understand the behavior of this operation.

Keys Must Be Immutable

Only immutable types can be used as keys in a hash table, and this is crucial.

Immutable types mean that once an object is created, its value cannot be changed. For instance, in Java, types like String and Integer are immutable. Once these objects are created, you can only read their values, not modify them.

In contrast, Java's ArrayList and LinkedList objects allow unrestricted addition and deletion of elements after creation, so they are mutable types.

Therefore, you can use String objects as hash table keys, but not ArrayList objects:

// Immutable types can be used as keys
Map<String, AnyOtherType> map1 = new HashMap<>();
Map<Integer, AnyOtherType> map2 = new HashMap<>();

// Mutable types should not be used as keys
// Note, this won't cause a syntax error, but the code is very likely to have bugs
Map<ArrayList<Integer>, AnyOtherType> map3 = new HashMap<>();

Why is it not recommended to use mutable types as key? For example, take this ArrayList. The implementation logic of its hashCode method is as follows:

public int hashCode() {
    for (int i = 0; i < elementData.length; i++) {
        h = 31 * h + elementData[i];
    }
}

The first issue is efficiency. Every time hashCode is calculated, it requires traversing the entire array, resulting in a complexity of $O(N)$. This can degrade the complexity of add, delete, search, and update operations in a hash table to $O(N)$.

A more severe issue is that the hashCode of an ArrayList is computed based on its elements. If you add or remove elements from this ArrayList, or if the hashCode of any element changes, the hashCode return value of the ArrayList will also change.

For instance, if you use an ArrayList variable arr as a key in a hash table to store a corresponding value, and then an element in arr is modified elsewhere in the program, the hashCode of arr will change. At this point, if you use this arr variable to query the hash table, you will find no corresponding value.

In other words, the key-value pair you stored in the hash table is unexpectedly lost, which is a very serious bug and can lead to potential memory leaks.

public class Test {
    public static void main(String[] args) {
        // Incorrect example
        // Using mutable types as keys in HashMap
        Map<ArrayList<Integer>, Integer> map = new HashMap<>();

        ArrayList<Integer> arr = new ArrayList<>();
        arr.add(1);
        arr.add(2);

        map.put(arr, 999);
        System.out.println(map.containsKey(arr)); // true
        System.out.println(map.get(arr)); // 999

        arr.add(3);
        // Serious bug occurs, key-value pair is lost
        System.out.println(map.containsKey(arr)); // false
        System.out.println(map.get(arr)); // null

        // At this point, the key-value pair for arr
        // still exists in the underlying table of
        // But because the hashCode of arr has changed, this key-value pair cannot be found
        // This can also cause a memory leak because the arr
        // variable is referenced by the map and cannot be garbage
    }
}

The above is a simple example of an error. You might say, if you remove the element 3, doesn't the key-value pair arr -> 999 reappear? Or, by directly iterating over the underlying table array of the hash table, shouldn't you also be able to see this key-value pair?

Come on 🙏🏻, are you writing code or a ghost story? Now you see it, now you don't—is your hash table haunted?

Just joking. The truth is, mutable types inherently bring uncertainty. In the overwhelming complexity of code, how do you know where this arr gets modified?

The correct approach is to use immutable types as the key for a hash table, such as using String as the key. In Java, once a String object is created, its value cannot be changed, so you won't encounter the problem mentioned above.

The hashCode method for String also needs to iterate over all characters, but due to its immutability, this value can be cached after being computed once, eliminating the need for repeated calculations. Therefore, the average time complexity remains $O(1)$.

Here, I used Java as an example, but it's similar in other languages. You should consult the relevant documentation to understand how the standard library's hash table calculates object hash values to avoid similar issues.

Summary

The explanation above should have connected all the underlying principles of hash tables. Let's conclude the content of this article by simulating several interview questions:

1. Why do we often say that the efficiency of adding, deleting, searching, and updating in a hash table is $O(1)$?

Because the underlying structure of a hash table is an array operation. The primary time complexity comes from calculating the index using the hash function and resolving hash collisions. As long as the complexity of the hash function is $O(1)$ and hash collisions are resolved reasonably, the complexity of adding, deleting, searching, and updating remains $O(1)$.

2. Why does the traversal order of a hash table change?

Because when a hash table reaches a certain load factor, it expands, which changes the capacity of the underlying array. This also alters the indices calculated by the hash function, thus changing the traversal order.

3. Is the efficiency of adding, deleting, searching, and updating in a hash table always $O(1)$?

Not necessarily. As analyzed earlier, only when the complexity of the hash function is $O(1)$ and hash collisions are handled properly can the complexity of these operations be guaranteed to be $O(1)$. Hash collisions can be resolved with standard solutions. The key issue is the computational complexity of the hash function. If an incorrect key type is used, such as an ArrayList as a key, the complexity of the hash table can degrade to $O(N)$.

4. Why must immutable types be used as hash table keys?

Because the main operations of a hash table rely on the index calculated by the hash function. If the hash value of the key changes, it can cause key-value pairs to be lost unexpectedly, leading to severe bugs.

Having a basic understanding of the source code in the standard library of your programming language is essential to writing efficient code.

Next, I will guide you step-by-step to implement a simple hash table using the chaining method and linear probing method to deepen your understanding of hash tables.