Basic Terminology in Graph Theory

A graph is made up of several nodes (Vertex) and edges (Edge):

• Each node has a unique ID.
• Edges can be directed (Directed Graph) or undirected (Undirected Graph).
• Edges can have weights (Weighted Graph) or no weights (Unweighted Graph).

Edge Weight and Direction

The picture below shows a directed, unweighted graph:

There is a directed edge from node 1 to node 3, so you can go directly from node 1 to node 3. But since there is no edge from node 3 to node 1, you cannot go from 3 to 1 directly.

Here is an undirected, unweighted graph:

There is an undirected edge between node 1 and node 3, so you can go from 1 to 3 and also from 3 to 1.

You can think of an undirected graph as a "two-way graph". In code, we often use two directed edges to simulate an undirected edge.

Here is a directed, weighted graph:

Here is an undirected, weighted graph:

Weighted graphs are very common. For example, in map apps, the edge weight can be the distance between two locations. In a logistics network, the edge weight can be the shipping cost.

There are many important algorithms based on weighted graphs, like finding the shortest path, minimum spanning tree, and so on. We will explain these in later sections.

Degree

Each node in a graph has a degree.

In undirected graphs, the degree is the number of edges connected to a node.

For example, in the graph below, node 1 has degree 2, node 4 has degree 4.

In directed graphs, because edges have directions, each node has indegree and outdegree.

For example, in the directed graph below, node 3 has indegree 2 (two edges point to it), and outdegree 1 (it points to one other node):

Number of Edges and Nodes

Usually, we talk about simple graphs: graphs without self-loops and without multiple edges.

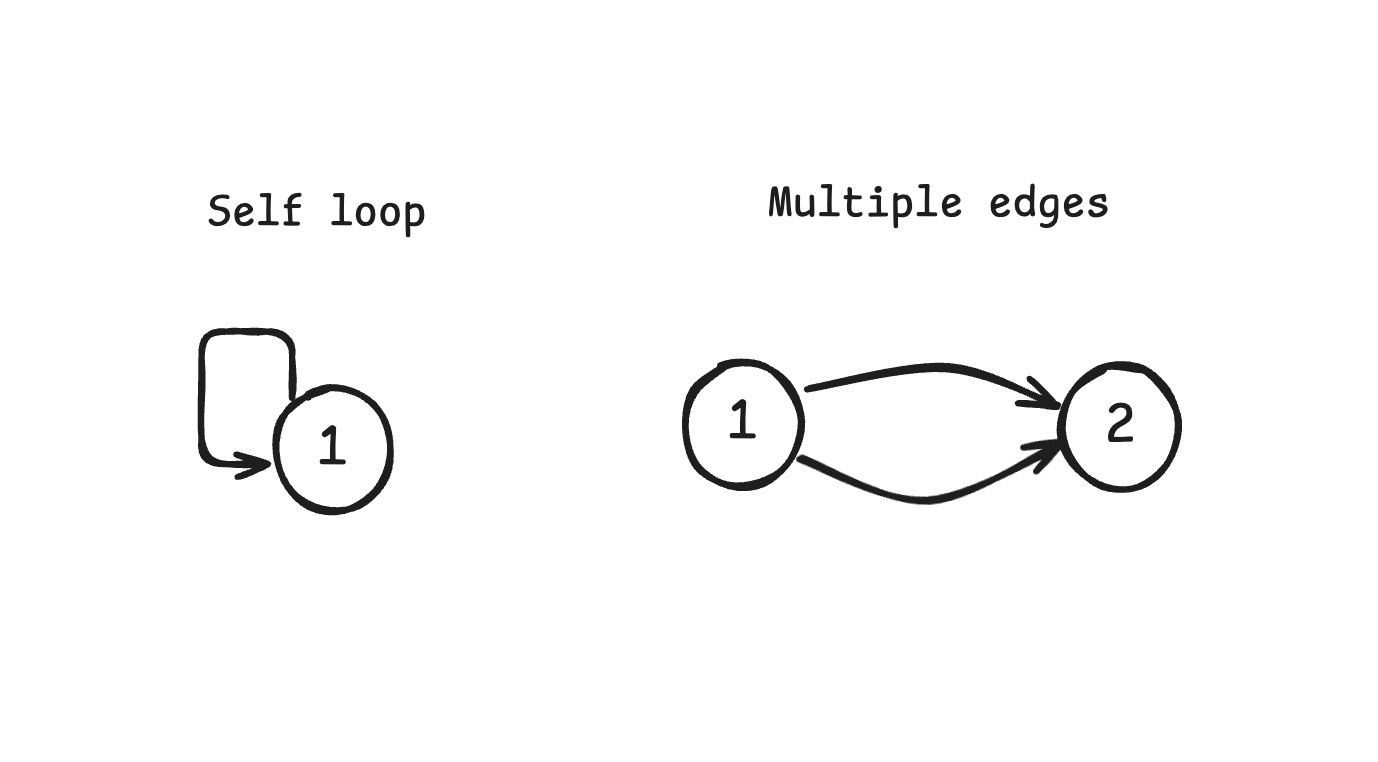
In a simple graph with $V$ nodes and $E$ edges, what is the possible range of $E$?

The minimum $E$ is 0. That means there are just isolated nodes, no edges.

For the maximum $E$, every node can connect to $V-1$ other nodes, so the maximum number of edges is $E = V(V-1)/2 \approx V^2$.

If almost every pair of nodes has an edge (so $E$ is close to $V^2$), this is called a dense graph. If there are few edges ($E$ much less than $V^2$), this is a sparse graph.

Subgraphs

In graph theory, the subgraph is an important concept.

Subgraph: If all nodes and edges of graph $G'$ are in graph $G$, then $G'$ is a subgraph of $G$. In short, a subgraph is made by removing some nodes or edges from the original graph.

Suppose the graph above is $G$. Let's look at two special types of subgraph:

Spanning Subgraph: This subgraph keeps all the nodes of the original graph, but includes only some edges.

Below is a spanning subgraph of $G$. It keeps all nodes, but removes the edge between nodes 3 and 4.

Induced Subgraph: Select some nodes from the original graph, and include all edges between those nodes as in the original graph.

Below is an induced subgraph of $G$, containing nodes 1,2,3,4 and all the edges among them from the original graph.

The idea of subgraph is often used in graph problems. For example, when we try to find a minimum spanning tree, we are looking for a spanning subgraph with all nodes and the smallest total weight.

Connectivity

Connectivity is a key concept in graph theory. It means whether there is a path between nodes.

Connectivity in Undirected Graphs

Connected Graph: If there is a path between any two nodes in the undirected graph, the graph is connected.

The graph above is a connected graph. You can start from any node and reach all others.

Connected Component: For an undirected graph that is not fully connected, its connected parts are called connected components. A graph can have more than one connected component.

For example, the graph below has two connected components: nodes 1~5 form one component, nodes 6,7 form another.

Connectivity in Directed Graphs

The idea of connectivity in directed graphs is a bit more complex. Because of edge directions, there are two types: strong and weak connectivity.

Strongly Connected Graph: If there is a directed path between every pair of nodes, the directed graph is strongly connected.

For example, the graph below is strongly connected. You can go from any node and reach all the others following the directions.

Weakly Connected Graph: If you ignore edge directions, and the graph becomes connected, then the directed graph is weakly connected.

For example, the graph below is not strongly connected (you can't go from node 4 to node 1), but if you ignore directions, all nodes are connected, so it's weakly connected.

Strongly Connected Component (SCC): In a directed graph, the biggest strongly connected subgraphs are called strongly connected components.

For example, the graph below has two strongly connected components: nodes 1~3 form one SCC, nodes 4~6 form another.

Weakly Connected Component (WCC): If you turn all directed edges in a directed graph to undirected edges, the connected components you get are called weakly connected components.

There are many other complex terms in graph theory, but the concepts above are enough for learning data structures and algorithms. Later, when we study specific graph algorithms, we will use these terms in real problems.