Binary Tree Recursive/Level Traversal
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 102. Binary Tree Level Order Traversal | 🟠 |
| 144. Binary Tree Preorder Traversal | 🟢 |
| 145. Binary Tree Postorder Traversal | 🟢 |
| 94. Binary Tree Inorder Traversal | 🟢 |
Prerequisites
Before reading this article, you should first learn:
One Sentence Summary
There are only two ways to traverse a binary tree: recursive traversal and level-order traversal. Recursive traversal leads to DFS algorithms, and level-order traversal leads to BFS algorithms.
The order of recursive traversal in a binary tree is fixed, but there are three key places to insert code. Placing code in different positions will produce different effects.
The order of level-order traversal is also fixed, but there are three different ways to write it, suitable for different situations.
After learning basic concepts of binary trees and special types of binary trees, this article will show you how to traverse and visit nodes in a binary tree.
There are two main traversal algorithms for binary trees: recursive traversal and level-order traversal. Each has a code template. The recursive template can be used for later DFS and backtracking algorithms. The level-order template can be used for BFS algorithms. That's why I often say binary tree structures are very important.
Preorder, inorder, and postorder traversals are all recursive traversals. The difference is just where you put your custom code in the template. I will explain this with a visual panel below.
Recursive Traversal (DFS)
Here is the code template for recursive traversal of a binary tree:
// basic binary tree node
class TreeNode {
int val;
TreeNode left, right;
}
// recursive traversal framework for binary tree
void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
traverse(root.right);
}// basic binary tree node
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
// recursive traversal framework for binary tree
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
traverse(root->left);
traverse(root->right);
}# basic binary tree node
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# recursive traversal framework for binary tree
def traverse(root: TreeNode):
if root is None:
return
traverse(root.left)
traverse(root.right)// basic binary tree node
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// recursive traversal framework for binary tree
func traverse(root *TreeNode) {
if root == nil {
return
}
traverse(root.Left)
traverse(root.Right)
}// basic binary tree node
class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
// recursive traversal framework for binary tree
var traverse = function(root) {
if (root === null) {
return;
}
traverse(root.left);
traverse(root.right);
}Why can this short and simple code traverse a binary tree? In what order does it visit the nodes?
You can think of the traverse recursive function as a pointer moving around the binary tree. The visualization panel below shows how this algorithm works step by step.
Open this panel. On the right, the root pointer shows the current node for the traverse function. You can click the line console.log("enter" several times to watch how the root pointer moves through the tree:
Recursive Traversal of a Binary Tree
Take your time. Watch the visualization as many times as you need until you fully understand the order in which the traverse function visits the nodes of the binary tree.
The order is: always go left first until you hit a null pointer and can't go further, then try to go right once; then keep going left again, and so on. If both left and right are done, return to the parent node.
From the code, you can see that root.left is called first, then root.right. Each time the traverse function is called, it goes to the left child first, until it cannot go further, then it tries the right child.
Now, let's try a small change. If we modify the traverse function to call root.right first, then root.left, what will happen?
// modify the standard binary tree traversal framework
void traverseFlip(TreeNode root) {
if (root == null) {
return;
}
// traverse the right subtree first, then traverse the left subtree
traverseFlip(root.right);
traverseFlip(root.left);
}// modify the standard binary tree traversal framework
void traverseFlip(TreeNode* root) {
if (root == nullptr) {
return;
}
// traverse the right subtree first, then traverse the left subtree
traverseFlip(root->right);
traverseFlip(root->left);
}# modify the standard binary tree traversal framework
def traverseFlip(root: TreeNode) -> None:
if root is None:
return
# traverse the right subtree first, then traverse the left subtree
traverseFlip(root.right)
traverseFlip(root.left)// modify the standard binary tree traversal framework
func traverseFlip(root *TreeNode) {
if root == nil {
return
}
// traverse the right subtree first, then traverse the left subtree
traverseFlip(root.Right)
traverseFlip(root.Left)
}// modify the standard binary tree traversal framework
var traverseFlip = function(root) {
if (root === null) {
return
}
// traverse the right subtree first, then traverse the left subtree
traverseFlip(root.right)
traverseFlip(root.left)
}Think about the order in which this function visits the tree nodes. Then, open the visualization below and click the line if (root === null) several times. Watch how the root pointer moves. Is it what you expected?
Algorithm Visualization
You can see that the traverseFlip function also visits all nodes in the tree, but the order is the opposite of the standard traverse function.
This example shows:
The order of recursive traversal (the way the root moves through the tree) only depends on the order of the left and right recursive calls, and nothing else.
Normally, we don't traverse a binary tree like traverseFlip. By default, we use the left-first, right-second order. So when we talk about the code template for tree traversal, we mean left first, right second:
// basic binary tree node
class TreeNode {
int val;
TreeNode left, right;
}
// recursive traversal framework for binary tree
void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
traverse(root.right);
}// basic binary tree node
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
// recursive traversal framework for binary tree
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
traverse(root->left);
traverse(root->right);
}# basic binary tree node
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# recursive traversal framework for binary tree
def traverse(root: TreeNode):
if root is None:
return
traverse(root.left)
traverse(root.right)// basic binary tree node
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// recursive traversal framework for binary tree
func traverse(root *TreeNode) {
if root == nil {
return
}
traverse(root.Left)
traverse(root.Right)
}// basic binary tree node
class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
// recursive traversal framework for binary tree
var traverse = function(root) {
if (root === null) {
return;
}
traverse(root.left);
traverse(root.right);
}As long as this left-first, right-second order doesn't change, the order in which traverse visits the nodes is fixed, no matter how many extra lines you add.
Some readers with data structure background may feel confused:
Wait, if you have taken a data structure course, you know binary trees have preorder, inorder, and postorder traversals, which give different orders. Why do you say the recursive traversal order is fixed?
That's a good question. Let's explain it next.
Understanding Preorder, Inorder, and Postorder Traversal
The order of recursive traversal, that is, the order in which the traverse function visits nodes, is fixed. As shown in the visual panel, the root pointer moves around the tree in a fixed order:
Algorithm Visualization
However, where you write your code inside the traverse function can make a difference. The results of preorder, inorder, and postorder traversals are different because you place the code at different positions in the function.
For example, when you just enter a node, you do not know anything about its child nodes. But when you are about to leave a node, all its child nodes have been visited. So, code written in these two situations will behave differently.
Preorder, inorder, and postorder traversal are really about where you put your code in the binary tree traversal framework:
// Binary tree traversal framework
void traverse(TreeNode root) {
if (root == null) {
return;
}
// pre-order position
traverse(root.left);
// in-order position
traverse(root.right);
// post-order position
}// binary tree traversal framework
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
// pre-order position
traverse(root->left);
// in-order position
traverse(root->right);
// post-order position
}# Binary tree traversal framework
def traverse(root):
if root is None:
return
# Pre-order position
traverse(root.left)
# In-order position
traverse(root.right)
# Post-order position// Binary tree traversal framework
func traverse(root *TreeNode) {
if root == nil {
return
}
// Preorder position
traverse(root.Left)
// Inorder position
traverse(root.Right)
// Postorder position
}// binary tree traversal framework
var traverse = function(root) {
if (root === null) {
return;
}
// pre-order position
traverse(root.left);
// in-order position
traverse(root.right);
// post-order position
};Code at the preorder position runs when you enter the node. Code at the inorder position runs after the left subtree is done but before the right subtree starts. Code at the postorder position runs after both left and right subtrees are done:
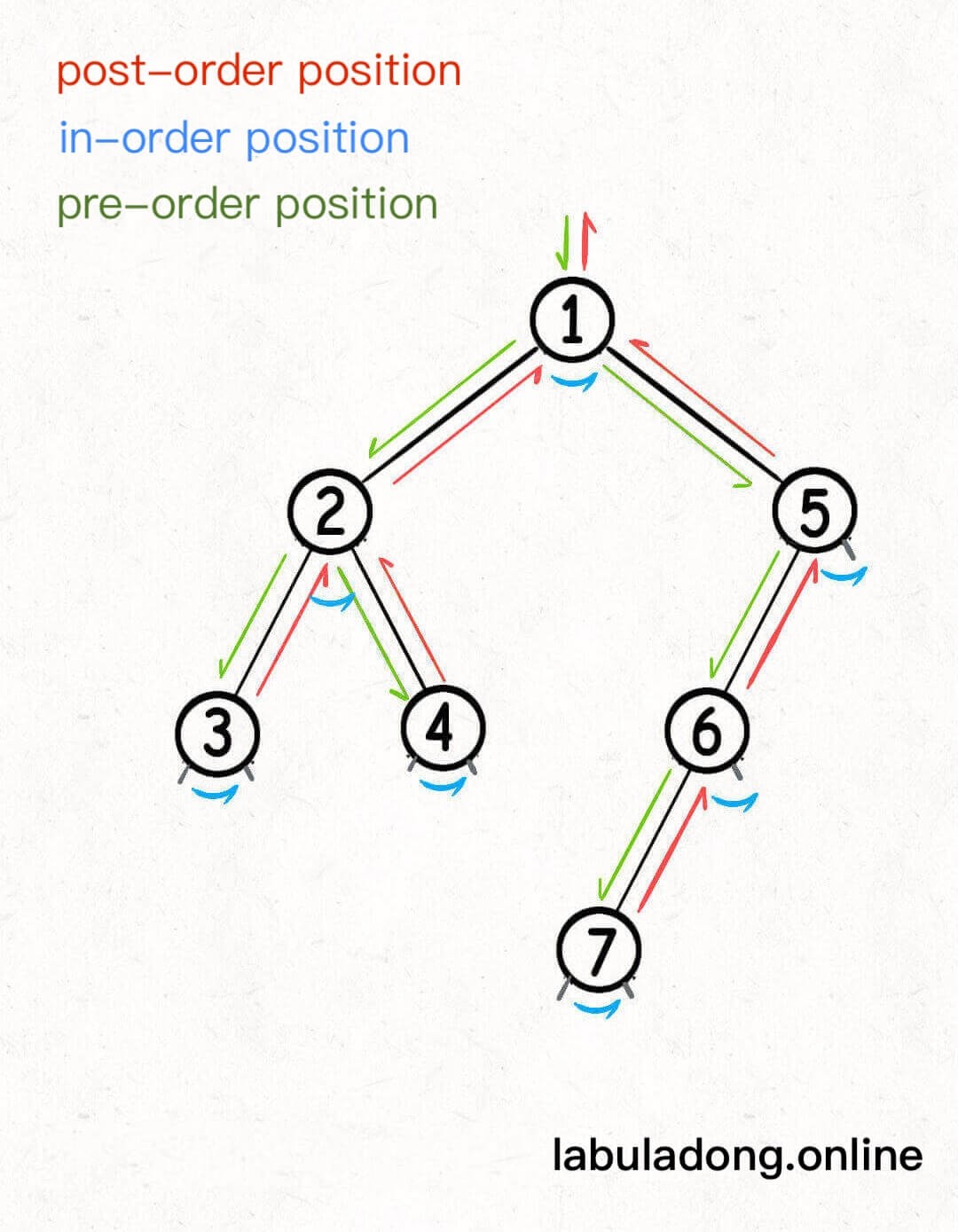
With the visualization, you can easily understand this.
Open the visual panel below. Click the line if (root == null) several times. You will see the root pointer moving around the tree in a fixed order. The order in which nodes turn green is the result of preorder traversal, because the code runs as soon as you enter a node. So the preorder sequence matches the order in which the root moves through the tree.
Preorder Traversal of a Binary Tree
Code at the inorder position runs after the left subtree is done but before the right subtree. Open the visual panel below. Click if (root == null) several times. You will see the root pointer movement is the same as before, but the order in which nodes turn blue is the result of inorder traversal—nodes turn blue when their left subtree is fully visited.
Inorder Traversal of a Binary Tree
Code at the postorder position runs after both the left and right subtrees are finished, right before leaving the node. Open the visual panel below. Click if (root == null) several times. The order in which nodes turn red is the result of postorder traversal—nodes only turn red after both left and right subtrees are done.
Postorder Traversal of a Binary Tree
It is very important to understand preorder, inorder, and postorder positions. Please carefully study the visual panels above, so you can figure out the preorder, inorder, and postorder results in your head for any binary tree.
Key Points
The main difference between the three positions is when the code is run.
In real algorithm problems, you won't just be asked to calculate preorder, inorder, or postorder results. You need to put the correct code in the correct position to solve problems. So, you must fully understand what effect code in each position has to write accurate solutions.
I will discuss the framework of binary tree traversal and how to use preorder, inorder, and postorder positions for backtracking and dynamic programming in Binary Tree Algorithm Ideas and the related exercises.
Now, you should be able to finish these LeetCode problems: 144. Binary Tree Preorder Traversal, 94. Binary Tree Inorder Traversal, 145. Binary Tree Postorder Traversal.
One more important point: for Binary Search Trees (BST), the result of an inorder traversal is always sorted. This is a key property of BST.
Check out the visual panel below. Click the line res.push(root.val);. You will see the order in which nodes are visited during an inorder traversal.
Inorder Traversal of BST Is Sorted
Later, in the BST Exercise Collection, you will find problems that use this property.
Level Order Traversal (BFS)
Earlier, we talked about recursive traversal, which uses the function call stack to traverse a binary tree. It visits the tree from left to right, column by column.
Level order traversal, as the name suggests, visits the binary tree level by level:
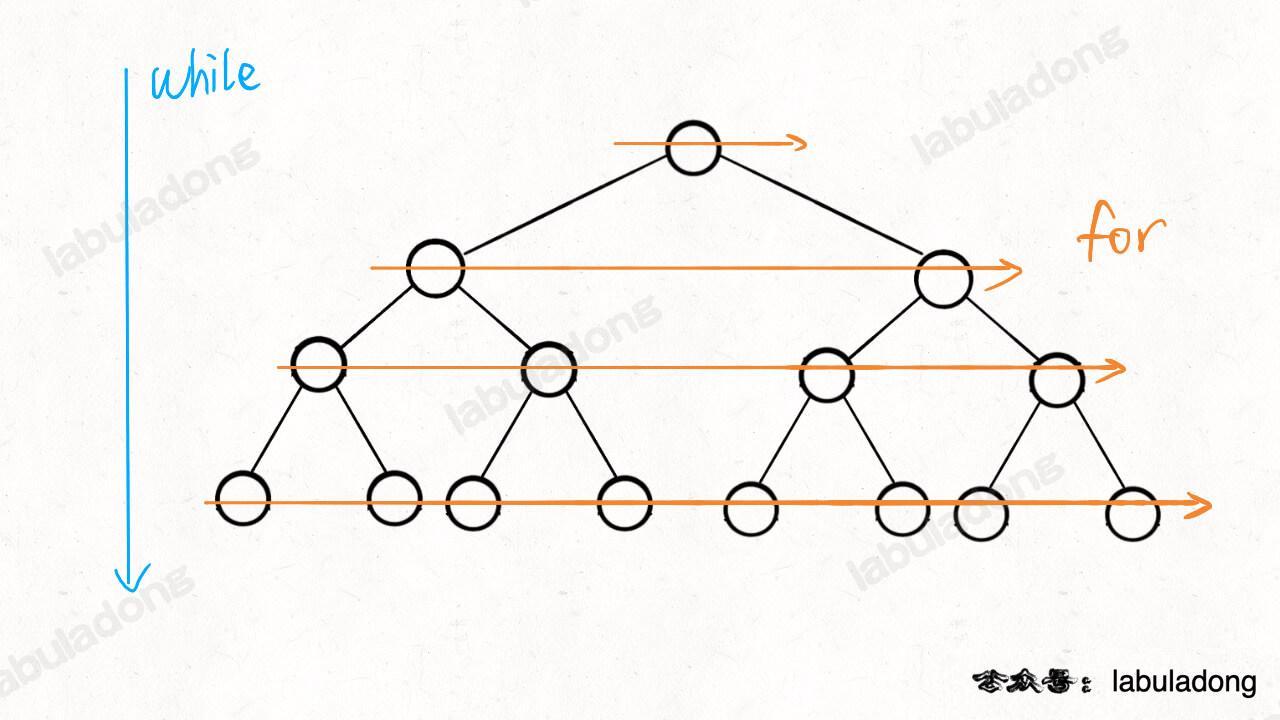
Level order traversal uses a queue. Depending on your needs, there are three common ways to write it. Let's look at them one by one.
Method 1
This is the simplest way. Here is the code:
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
// visit the cur node
System.out.println(cur.val);
// add the left and right children of cur to the queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
std::queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* cur = q.front();
q.pop();
// visit the cur node
std::cout << cur->val << std::endl;
// add the left and right children of cur to the queue
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
}from collections import deque
def levelOrderTraverse(root):
if root is None:
return
q = deque()
q.append(root)
while q:
cur = q.popleft()
# visit cur node
print(cur.val)
# add cur's left and right children to the queue
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []*TreeNode{}
q = append(q, root)
for len(q) > 0 {
cur := q[0]
q = q[1:]
// visit cur node
fmt.Println(cur.Val)
// add cur's left and right children to the queue
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
}var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
var q = [];
q.push(root);
while (q.length !== 0) {
var cur = q.shift();
// visit cur node
console.log(cur.val);
// add cur's left and right children to the queue
if (cur.left !== null) {
q.push(cur.left);
}
if (cur.right !== null) {
q.push(cur.right);
}
}
}You can open this visual panel and click on the line while (q.length > 0) to see how the cur variable moves through the tree. You will see that the nodes are visited level by level, from left to right.
Level Order Traversal of a Binary Tree
Pros and Cons of This Method
The biggest advantage is simplicity. Each time, you take the front node from the queue and add its left and right children to the queue.
The downside is you cannot know which level the current node is on. Knowing the node's level is often needed, for example, to collect nodes of each level or to calculate the minimum depth of the tree.
So, this method is simple but not used much. The next method is more common.
Method 2
If you change method 1 a bit, you get this version:
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// record the current level being traversed (root node is considered as level 1)
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// visit the cur node and know its level
System.out.println("depth = " + depth + ", val = " + cur.val);
// add the left and right children of cur to the queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<TreeNode*> q;
q.push(root);
// record the current level being traversed (the root node is considered as level 1)
int depth = 1;
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode* cur = q.front();
q.pop();
// visit the cur node, knowing its level
cout << "depth = " << depth << ", val = " << cur->val << endl;
// add the left and right children of cur to the queue
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
depth++;
}
}from collections import deque
def levelOrderTraverse(root):
if root is None:
return
q = deque()
q.append(root)
# record the current depth being traversed (root node is considered as level 1)
depth = 1
while q:
sz = len(q)
for i in range(sz):
cur = q.popleft()
# visit cur node and know its depth
print(f"depth = {depth}, val = {cur.val}")
# add cur's left and right children to the queue
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
depth += 1func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []*TreeNode{root}
// record the current depth being traversed (root node is considered as level 1)
depth := 1
for len(q) > 0 {
// get the current queue length
sz := len(q)
for i := 0; i < sz; i++ {
// dequeue the front of the queue
cur := q[0]
q = q[1:]
// visit the cur node and know its depth
fmt.Printf("depth = %d, val = %d\n", depth, cur.Val)
// add cur's left and right children to the queue
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
depth++
}
}var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
let q = [];
q.push(root);
// record the current depth (root node is considered as level 1)
let depth = 1;
while (q.length !== 0) {
let sz = q.length;
for (let i = 0; i < sz; i++) {
let cur = q.shift();
// visit the cur node and know its depth
console.log("depth = " + depth + ", val = " + cur.val);
// add the left and right children of cur to the queue
if (cur.left !== null) {
q.push(cur.left);
}
if (cur.right !== null) {
q.push(cur.right);
}
}
depth++;
}
};Notice the inner for loop in the code:
int sz = q.size();
for (int i = 0; i < sz; i++) {
...
}The variable i records the position of node cur in the current level. In most problems, you do not need i, so you can also write it like this:
int sz = q.size();
while (sz-- > 0) {
...
}This is just a small detail, use whichever you like.
But remember, you must save the queue length sz before the loop starts. The length of the queue changes during the loop, so you cannot use q.size() directly in the loop condition.
You can open this visual panel and click on the line console.log to see how the cur variable moves through the tree. You will see nodes visited level by level, from left to right, and now you can also see the level number of each node.
Level Order Traversal of a Binary Tree 2
With this method, you can record the level of each node. It can solve problems like finding the minimum depth of a binary tree. This is the most common way to write level order traversal.
Method 3
If method 2 is the most common, why do we need method 3? It is to prepare for more advanced topics later.
Now we are only talking about level order traversal of binary trees. But level order traversal can also be used for N-ary trees, BFS of graphs, and the classic BFS brute-force algorithm. So, let's extend a bit.
In method 2, each time we go down one level, we increase depth by 1. You can think of each edge as having a weight of 1. The depth of each node is the sum of edge weights from the root to that node. All nodes at the same level have the same depth.
Now, suppose each edge can have any weight, and you want to print the total path weight for each node during level order traversal. What should you do?
In this case, nodes on the same level may have different total weights. Just one depth variable is not enough.
Method 3 solves this problem. It adds a State class to method 1, so each node keeps track of its own total path weight. Here is the code:
class State {
TreeNode node;
int depth;
State(TreeNode node, int depth) {
this.node = node;
this.depth = depth;
}
}
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<State> q = new LinkedList<>();
// the path weight sum of the root node is 1
q.offer(new State(root, 1));
while (!q.isEmpty()) {
State cur = q.poll();
// visit the cur node, while knowing its path weight sum
System.out.println("depth = " + cur.depth + ", val = " + cur.node.val);
// add the left and right child nodes of cur to the queue
if (cur.node.left != null) {
q.offer(new State(cur.node.left, cur.depth + 1));
}
if (cur.node.right != null) {
q.offer(new State(cur.node.right, cur.depth + 1));
}
}
}class State {
public:
TreeNode* node;
int depth;
State(TreeNode* node, int depth) : node(node), depth(depth) {}
};
void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<State> q;
// the path weight sum of the root node is 1
q.push(State(root, 1));
while (!q.empty()) {
State cur = q.front();
q.pop();
// visit the cur node, while knowing its path weight sum
cout << "depth = " << cur.depth << ", val = " << cur.node->val << endl;
// add the left and right children of cur to the queue
if (cur.node->left != nullptr) {
q.push(State(cur.node->left, cur.depth + 1));
}
if (cur.node->right != nullptr) {
q.push(State(cur.node->right, cur.depth + 1));
}
}
}class State:
def __init__(self, node, depth):
self.node = node
self.depth = depth
def levelOrderTraverse(root):
if root is None:
return
q = deque()
# the path weight sum of the root node is 1
q.append(State(root, 1))
while q:
cur = q.popleft()
# visit the cur node, and know its path weight sum
print(f"depth = {cur.depth}, val = {cur.node.val}")
# add the left and right child nodes of cur to the queue
if cur.node.left is not None:
q.append(State(cur.node.left, cur.depth + 1))
if cur.node.right is not None:
q.append(State(cur.node.right, cur.depth + 1))type State struct {
node *TreeNode
depth int
}
func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []State{{root, 1}}
for len(q) > 0 {
cur := q[0]
q = q[1:]
// visit the cur node, also know its path weight sum
fmt.Printf("depth = %d, val = %d\n", cur.depth, cur.node.Val)
// add cur's left and right children to the queue
if cur.node.Left != nil {
q = append(q, State{cur.node.Left, cur.depth + 1})
}
if cur.node.Right != nil {
q = append(q, State{cur.node.Right, cur.depth + 1})
}
}
}function State(node, depth) {
this.node = node;
this.depth = depth;
}
var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
// @visualize bfs
var q = [];
// the path weight sum of the root node is 1
q.push(new State(root, 1));
while (q.length !== 0) {
var cur = q.shift();
// visit the cur node, while knowing its path weight sum
console.log("depth = " + cur.depth + ", val = " + cur.node.val);
// add the left and right children of cur to the queue
if (cur.node.left !== null) {
q.push(new State(cur.node.left, cur.depth + 1));
}
if (cur.node.right !== null) {
q.push(new State(cur.node.right, cur.depth + 1));
}
}
};You can open this visual panel and click on the line console.log to see the traversal. You will see nodes visited level by level, from left to right, and you can also see the level number of each node.
Level Order Traversal of a Binary Tree 3
With this method, every node has its own depth variable. It is the most flexible and can meet all BFS needs. But you need to define a State class, which can be a bit troublesome. If not needed, just use method 2.
Soon you will learn that this kind of weighted edge problem belongs to graph algorithms. You will use this method in BFS exercises and Dijkstra's algorithm.
Other Traversal Methods?
There are only these two ways to traverse a binary tree. Other code may look different, but the core idea is always one of these two methods.
For example, you might see code that uses a stack to traverse a binary tree. But this is actually still recursive traversal; the stack just simulates the call stack.
Or, you might see code that uses recursion to visit each level. This is still level order traversal, just written differently.
In short, don't be fooled by appearances. There are just two ways to traverse a binary tree. Once you master them with the following tutorials and exercises, brute-force algorithms will be easy for you.