Binary Tree Basic and Common Types

Prerequisite Knowledge

Before reading this article, you need to study:

Linked List Basics

I think the binary tree is the most important basic data structure, without exception.

If you are a beginner, it's hard for me to fully explain why at this stage. You need to study more content on this site to understand it. I will give you two simple reasons for now:

The binary tree itself is a simple data structure, but many complicated data structures are based on it, such as red-black tree (binary search tree), multi-way tree, binary heap, graph, trie, union-find set, segment tree, and so on. If you master the binary tree, these data structures will not be a problem. If you don't, it will be hard to learn more advanced data structures.
The binary tree is not just a data structure, but also a way of algorithm thinking. Many brute-force algorithms, such as backtracking, BFS algorithm, dynamic programming, in essence, turn problems into a tree structure. Once you can abstract the problem into a tree, it becomes a binary tree problem. Looking at code, others may see a bunch of text and get confused, but with this way of thinking, you will see the code as a tree. You will know how to change it, and it will become much easier.

The following chapters include many explanations and exercises about binary trees. Follow the order of this site, and I will help you fully understand binary trees. Then, you will see why I value binary trees so much.

Several Common Types of Binary Trees

The main difficulty with binary trees is in solving algorithm problems. The structure itself is simple, just a type of tree structure like this:

This is a normal binary tree. You should understand a few common terms:

The nodes directly connected below a node are child nodes. The node directly above is the parent node. For example, node 3's parent is 1, its left child is 5, and its right child is 6. Node 5's parent is 3, its left child is 7, and it has no right child.
The tree that uses a child node as its root is called a subtree. For example, the left subtree of node 3 is made up of node 5 and 7. The right subtree includes node 6 and 8.
The topmost node without a parent (node 1) is called the root node. The nodes at the bottom with no children (4, 7, 8) are called leaf nodes.
The number of nodes from the root node to a leaf node is the maximum depth or height of the tree. For the tree above, the max depth is 4, which is the path from root node 1 to leaf 7 or 8.

That's all. It's that simple.

There are some special types of binary trees with their own names. You need to know these so that when you see these terms in problems, you won't be confused.

Full Binary Tree

Look at the picture for a clear idea. A full binary tree has every level completely filled. The whole tree looks like a triangle:

The full binary tree has an advantage: it's easy to count the number of nodes. If the depth is h, then the total number of nodes is 2^h - 1. This comes from the geometric series.

Complete Binary Tree

A complete binary tree means that every level is filled from left to right, and except for the last level, all other levels are fully filled:

As you can see, a full binary tree is actually a special case of a complete binary tree.

Feature of complete binary tree: Because the nodes are packed tightly, if you number the nodes from left to right and top to bottom, there is a clear pattern in the index of parent and child nodes.

This feature will be used when talking about binary heap basics and segment tree basics: you can use an array to store a complete binary tree. You don't need to build a linked node structure.

There is another property of complete binary trees: the left and right subtrees of a complete binary tree are also complete binary trees.

Or to be more precise: at least one of the left or right subtrees of a complete binary tree is a full binary tree.

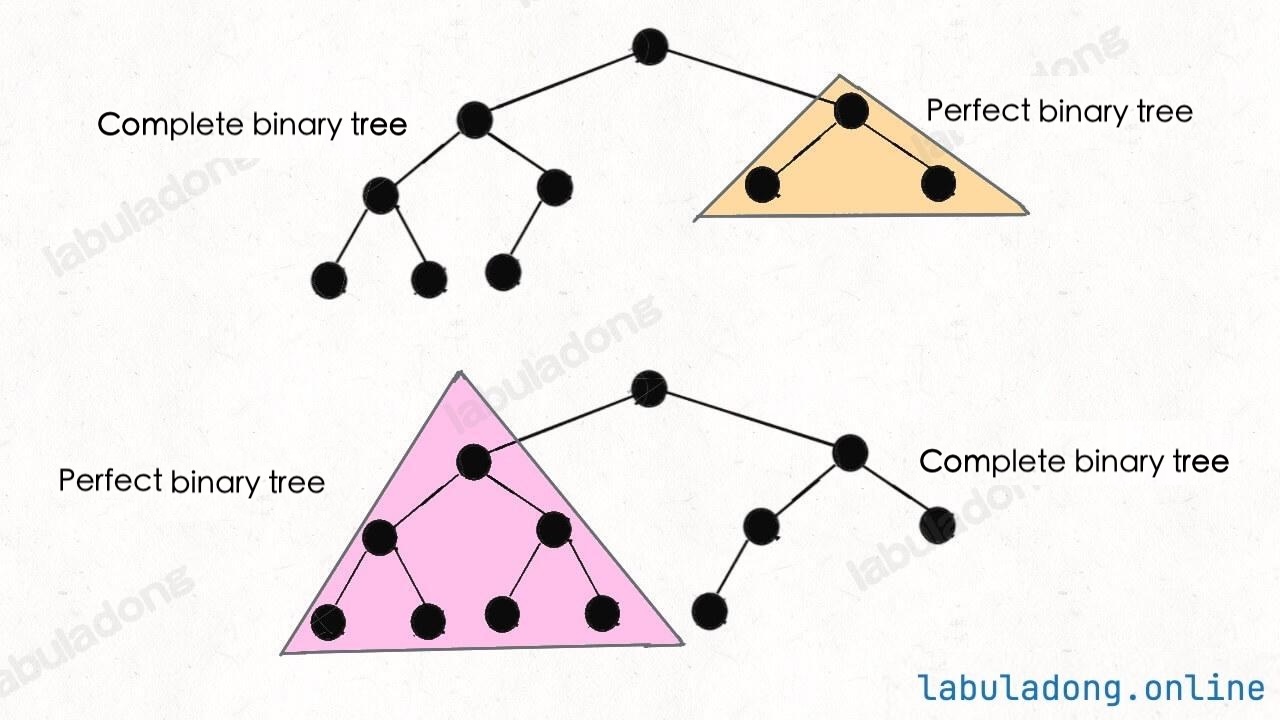
This property is useful when solving algorithm problems, such as counting the number of nodes in a complete binary tree. Here we just mention it briefly.

Binary Search Tree

A Binary Search Tree (BST) is a very common binary tree. Its definition is:

For every node in the tree, all nodes in its left subtree have values less than the value of the node, and all nodes in its right subtree have values greater than the value of the node. You can simply remember it as "left is smaller, right is bigger."

I made "all nodes in the subtree" bold because it's a common mistake for beginners. Don't just look at the child nodes, but the whole subtree.

For example, the tree below is a BST:

All nodes in the left subtree of node 7 have values less than 7, and all nodes in the right subtree have values greater than 7. The same rule applies to node 4 and so on.

On the other hand, the following tree is not a BST:

If you only look at the left and right child of each node, it seems fine. But you should look at the entire subtree. Notice that in the left subtree of node 7, there is a node 8 which is bigger than 7. This does not meet the definition of a BST.

BST is a very useful data structure. Because of the "left smaller, right bigger" property, we can quickly find a specific node or all nodes within a range in a BST. This is the advantage of BST.

For example, in a normal binary tree with no value order, if you want to find a node with value x, you have to traverse the whole tree from the root.

But in a BST, you can compare the root node with x. If x is bigger than the root, you can skip the entire left subtree and start searching from the right subtree. This helps you quickly locate the node with value x.

We will have a special chapter later to explain BST in detail, with many exercises. For now, just remember these basic ideas.

Height-Balanced Binary Tree

A Height-Balanced Binary Tree is a special kind of binary tree. For every node, the height difference between its left and right subtrees is at most 1.

Be careful: it must be true for every node, not just the root.

For example, in the tree below, the root node 1 has a left subtree height of 2 and a right subtree height of 3. Node 2 has a left subtree height of 1 and right subtree height of 0. Node 3 has a left subtree height of 2 and right subtree height of 1. For every node, the height difference is at most 1, so this is a height-balanced binary tree:

The following tree is not a height-balanced binary tree, because node 2 has a left subtree height of 2 and right subtree height of 0. The difference is more than 1, so it does not meet the rule:

If a height-balanced binary tree has $N$ nodes, its height is $O(\log N)$ . This is very important. In later chapters, we will talk about some data structures based on binary trees. If the tree's height is $O(\log N)$ , then add, delete, find, and update operations will be very fast.

But if the tree is not balanced, for example in this extreme case:

Then the tree is just like a linked list. The efficiency of operations like add, delete, and find will be much lower.

Self-Balanced Binary Tree

We just talked about height-balanced binary trees and how their height is $O(\log N)$ , so operations are efficient.

If we can adjust the tree structure while adding or deleting nodes to keep the height balanced, we get a self-balanced binary tree.

There are many ways to make a self-balanced binary tree. The most classic one is the Red-Black Tree, which is a kind of self-balancing binary search tree.

To keep the tree balanced, the key is the "rotation" operation. The visual panel below shows how rotation works in a red-black tree. You can click the code for left and right rotation to see the effect:

Algorithm Visualization

Ways to Implement a Binary Tree

The most common way to implement a binary tree is using a linked structure, similar to a linked list. Each node in the binary tree has pointers to its left and right children. This method is simple and easy to understand.

On LeetCode, the binary trees you see in problems are usually built in this way. The TreeNode class for a binary tree node usually looks like this:

java

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { this.val = x; }
}

// You can construct a binary tree like this:
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.left = new TreeNode(5);
root.right.right = new TreeNode(6);

// The constructed binary tree looks like this:
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

cpp

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// You can construct a binary tree like this:
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->right->left = new TreeNode(5);
root->right->right = new TreeNode(6);

// The constructed binary tree is like this:
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

python

class TreeNode:
    def __init__(self, x: int):
        self.val = x
        self.left = None
        self.right = None

# You can build a binary tree like this:
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.right.left = TreeNode(5)
root.right.right = TreeNode(6)

# The constructed binary tree looks like this:
#     1
#    / \
#   2   3
#  /   / \
# 4   5   6

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

// You can construct a binary tree like this:
root := &TreeNode{Val: 1}
root.Left := &TreeNode{Val: 2}
root.Right := &TreeNode{Val: 3}
root.Left.Left := &TreeNode{Val: 4}
root.Right.Left := &TreeNode{Val: 5}
root.Right.Right := &TreeNode{Val: 6}

// The constructed binary tree looks like this:
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

javascript

var TreeNode = function(x) {
    this.val = x;
    this.left = null;
    this.right = null;
}

// you can construct a binary tree like this:
var root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.left = new TreeNode(5);
root.right.right = new TreeNode(6);

// the constructed binary tree looks like this:
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

Since this is the common way, it means there are other ways to implement a binary tree, right?

Yes. In Binary Heap Basics and Union Find Algorithm Explained, we sometimes use an array to store a binary tree, depending on the needs of the problem.

When using the visualization panel to show recursive functions, the tool actually builds a recursion tree based on the function stack. This can also be seen as another way to represent a binary tree.

In some algorithm problems, we may abstract a real-world problem into a binary tree structure, but we do not need to actually create a tree with TreeNode. Instead, we can use a structure similar to a hash map to represent a binary tree or a multi-way tree.

For example, consider this binary tree:

We can use a hash map where the key is the parent node's id, and the value is a list of its children's ids (each node has a unique id). Each key-value pair represents a node in a multi-way tree. The tree can be represented like this:

java

// 1 -> [2, 3]
// 2 -> [4]
// 3 -> [5, 6]

HashMap<Integer, List<Integer>> tree = new HashMap<>();
tree.put(1, Arrays.asList(2, 3));
tree.put(2, Collections.singletonList(4));
tree.put(3, Arrays.asList(5, 6));

cpp

// 1 -> {2, 3}
// 2 -> {4}
// 3 -> {5, 6}

unordered_map<int, vector<int>> tree;
tree[1] = {2, 3};
tree[2] = {4};
tree[3] = {5, 6};

python

# 1 -> [2, 3]
# 2 -> [4]
# 3 -> [5, 6]

tree = {
    1: [2, 3],
    2: [4],
    3: [5, 6]
}

// 1 -> [2, 3]
// 2 -> [4]
// 3 -> [5, 6]

tree := map[int][]int{
    1: {2, 3},
    2: {4},
    3: {5, 6},
}

javascript

// 1 -> [2, 3]
// 2 -> [4]
// 3 -> [5, 6]

let tree = new Map([
    [1, [2, 3]],
    [2, [4]],
    [3, [5, 6]]
]);

This way, you can simulate and work with binary or multi-way trees. Later, when we talk about graph algorithms, you will see that this structure has a special name called an adjacency list.