动态规划之最小路径和

本文讲解的例题

LeetCode	力扣	难度
64. Minimum Path Sum	64. 最小路径和	🟠

前置知识

阅读本文前，你需要先学习：

动态规划核心框架

今天聊一道经典的动态规划题目，它是力扣第 64 题「最小路径和」：

64. 最小路径和 | 力扣 | LeetCode | 🟠

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

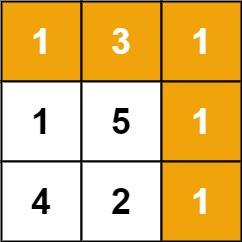
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200

题目来源：力扣 64. 最小路径和。

函数签名如下：

java

int minPathSum(int[][] grid);

cpp

int minPathSum(vector<vector<int>>& grid);

python

def minPathSum(grid: List[List[int]]) -> int

func minPathSum(grid [][]int) int {}

javascript

var minPathSum = function(grid) {}

其实这道题难度不算大，但你可能会遇到一些难度比较大的变体，所以统一讲一讲这种问题的通用思路。

一般来说，让你在二维矩阵中求最优化问题（最大值或者最小值），肯定需要递归 + 备忘录，也就是动态规划技巧。

就拿题目举的例子来说，我给图中的几个格子编个号方便描述：

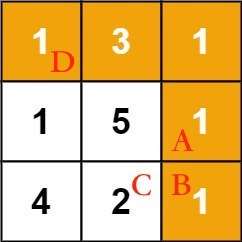
我们想计算从起点 D 到达 B 的最小路径和，那你说怎么才能到达 B 呢？

题目说了只能向右或者向下走，所以只有从 A 或者 C 走到 B。

那么算法怎么知道从 A 走到 B 才能使路径和最小，而不是从 C 走到 B 呢？

难道是因为位置 A 的元素大小是 1，位置 C 的元素是 2，1 小于 2，所以一定要从 A 走到 B 才能使路径和最小吗？

其实不是的，真正的原因是，从 D 走到 A 的最小路径和是 6，而从 D 走到 C 的最小路径和是 8，6 小于 8，所以一定要从 A 走到 B 才能使路径和最小。

换句话说，我们把「从 D 走到 B 的最小路径和」这个问题转化成了「从 D 走到 A 的最小路径和」和「从 D 走到 C 的最小路径和」这两个问题。

理解了上面的分析，这不就是状态转移方程吗？所以这个问题肯定会用到动态规划技巧来解决。

比如我们定义如下一个 dp 函数：

java

int dp(int[][] grid, int i, int j);

cpp

int dp(int grid[][], int i, int j);

python

def dp(grid: List[List[int]], i: int, j: int) -> int:

func dp(grid [][]int, i int, j int) int {}

javascript

var dp = function(grid, i, j) {}

这个 dp 函数的定义如下：

从左上角位置 (0, 0) 走到位置 (i, j) 的最小路径和为 dp(grid, i, j)。

根据这个定义，我们想求的最小路径和就可以通过调用这个 dp 函数计算出来：

java

int minPathSum(int[][] grid) {
    int m = grid.length;
    int n = grid[0].length;
    // 计算从左上角走到右下角的最小路径和
    return dp(grid, m - 1, n - 1);
}

cpp

int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size();
    int n = grid[0].size();
    // 计算从左上角走到右下角的最小路径和
    return dp(grid, m - 1, n - 1);
}

python

def minPathSum(grid: List[List[int]]) -> int:
    m = len(grid)
    n = len(grid[0])
    # 计算从左上角走到右下角的最小路径和
    return dp(grid, m - 1, n - 1)

func minPathSum(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    // 计算从左上角走到右下角的最小路径和
    return dp(grid, m-1, n-1)
}

javascript

var minPathSum = function(grid) {
    var m = grid.length;
    var n = grid[0].length;
    // 计算从左上角走到右下角的最小路径和
    return dp(grid, m - 1, n - 1);
};

再根据刚才的分析，很容易发现，dp(grid, i, j) 的值取决于 dp(grid, i - 1, j) 和 dp(grid, i, j - 1) 返回的值。

我们可以直接写代码了：

java

int dp(int[][] grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        return grid[0][0];
    }
    // 如果索引出界，返回一个很大的值，
    // 保证在取 min 的时候不会被取到
    if (i < 0 || j < 0) {
        return Integer.MAX_VALUE;
    }

    // 左边和上面的最小路径和加上 grid[i][j]
    // 就是到达 (i, j) 的最小路径和
    return Math.min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j];
}

cpp

int dp(vector<vector<int>>& grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        return grid[0][0];
    }
    // 如果索引出界，返回一个很大的值，
    // 保证在取 min 的时候不会被取到
    if (i < 0 || j < 0) {
        return INT_MAX;
    }

    // 左边和上面的最小路径和加上 grid[i][j]
    // 就是到达 (i, j) 的最小路径和
    return min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j];
}

python

def dp(grid: List[List[int]], i: int, j: int) -> int:
    # base case
    if i == 0 and j == 0:
        return grid[0][0]

    # 如果索引出界，返回一个很大的值，
    # 保证在取 min 的时候不会被取到
    if i < 0 or j < 0:
        return float('inf')

    # 左边和上面的最小路径和加上 grid[i][j]
    # 就是到达 (i, j) 的最小路径和
    return min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j]

func dp(grid [][]int, i int, j int) int {
    // base case
    if i == 0 && j == 0 {
        return grid[0][0]
    }
    // 如果索引出界，返回一个很大的值，
    // 保证在取 min 的时候不会被取到
    if i < 0 || j < 0 {
        return math.MaxInt32
    }

    // 左边和上面的最小路径和加上 grid[i][j]
    // 就是到达 (i, j) 的最小路径和
    return min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j]
}

func min(a int, b int) int {
    if a < b {
        return a
    }
    return b
}

javascript

var dp = function(grid, i, j) {
  // base case
  if (i == 0 && j == 0) {
    return grid[0][0];
  }
  // 如果索引出界，返回一个很大的值，
  // 保证在取 min 的时候不会被取到
  if (i < 0 || j < 0) {
    return Number.MAX_VALUE;
  }
  
  // 左边和上面的最小路径和加上 grid[i][j]
  // 就是到达 (i, j) 的最小路径和
  return Math.min(
    dp(grid, i - 1, j), 
    dp(grid, i, j - 1)
  ) + grid[i][j];
}

上述代码逻辑已经完整了，接下来就分析一下，这个递归算法是否存在重叠子问题？是否需要用备忘录优化一下执行效率？

前文多次说过判断重叠子问题的技巧，首先抽象出上述代码的递归框架：

int dp(int i, int j) {
    dp(i - 1, j); // #1
    dp(i, j - 1); // #2
}

如果我想从 dp(i, j) 递归到 dp(i-1, j-1)，有几种不同的递归调用路径？

可以是 dp(i, j) -> #1 -> #2 或者 dp(i, j) -> #2 -> #1，不止一种，说明 dp(i-1, j-1) 会被多次计算，所以一定存在重叠子问题。

那么我们可以使用备忘录技巧进行优化：

java

class Solution {
    int[][] memo;

    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        // 构造备忘录，初始值全部设为 -1
        memo = new int[m][n];
        for (int[] row : memo)
            Arrays.fill(row, -1);

        return dp(grid, m - 1, n - 1);
    }

    int dp(int[][] grid, int i, int j) {
        // base case
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        if (i < 0 || j < 0) {
            return Integer.MAX_VALUE;
        }
        // 避免重复计算
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // 将计算结果记入备忘录
        memo[i][j] = Math.min(
                dp(grid, i - 1, j),
                dp(grid, i, j - 1)
        ) + grid[i][j];

        return memo[i][j];
    }
}

cpp

#include <vector>
#include <algorithm>

class Solution {
public:
    std::vector<std::vector<int>> memo;

    int minPathSum(std::vector<std::vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        // 构造备忘录，初始值全部设为 -1
        memo.resize(m, std::vector<int>(n, -1));

        return dp(grid, m - 1, n - 1);
    }

    int dp(std::vector<std::vector<int>>& grid, int i, int j) {
        // base case
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        if (i < 0 || j < 0) {
            return INT_MAX;
        }
        // 避免重复计算
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // 将计算结果记入备忘录
        memo[i][j] = std::min(
                dp(grid, i - 1, j),
                dp(grid, i, j - 1)
        ) + grid[i][j];

        return memo[i][j];
    }
};

python

class Solution:
    def __init__(self):
        self.memo = None

    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        # 构造备忘录，初始值全部设为 -1
        self.memo = [[-1 for _ in range(n)] for _ in range(m)]

        return self.dp(grid, m - 1, n - 1)

    def dp(self, grid: List[List[int]], i: int, j: int) -> int:
        # base case
        if i == 0 and j == 0:
            return grid[0][0]
        if i < 0 or j < 0:
            return float('inf')
        # 避免重复计算
        if self.memo[i][j] != -1:
            return self.memo[i][j]
        # 将计算结果记入备忘录
        self.memo[i][j] = min(
            self.dp(grid, i - 1, j),
            self.dp(grid, i, j - 1)
        ) + grid[i][j]

        return self.memo[i][j]

var memo [][]int

func minPathSum(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    // 构造备忘录，初始值全部设为 -1
    memo = make([][]int, m)
    for i := range memo {
        memo[i] = make([]int, n)
        for j := range memo[i] {
            memo[i][j] = -1
        }
    }

    return dp(grid, m-1, n-1)
}

func dp(grid [][]int, i, j int) int {
    // base case
    if i == 0 && j == 0 {
        return grid[0][0]
    }
    if i < 0 || j < 0 {
        return int(^uint(0) >> 1) // Integer.MAX_VALUE equivalent in Go
    }
    // 避免重复计算
    if memo[i][j] != -1 {
        return memo[i][j]
    }
    // 将计算结果记入备忘录
    memo[i][j] = min(
        dp(grid, i-1, j),
        dp(grid, i, j-1),
    ) + grid[i][j]

    return memo[i][j]
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

javascript

var minPathSum = function(grid) {
    let m = grid.length;
    let n = grid[0].length;
    // 构造备忘录，初始值全部设为 -1
    let memo = Array.from({ length: m }, () => Array(n).fill(-1));

    // @visualize status(i,j)
    var dp = function(grid, i, j, memo) {
        // base case
        if (i === 0 && j === 0) {
            return grid[0][0];
        }
        if (i < 0 || j < 0) {
            return Number.MAX_VALUE;
        }
        // 避免重复计算
        if (memo[i][j] !== -1) {
            return memo[i][j];
        }
        // 将计算结果记入备忘录
        memo[i][j] = Math.min(
            dp(grid, i - 1, j, memo),
            dp(grid, i, j - 1, memo)
        ) + grid[i][j];

        return memo[i][j];
    }

    return dp(grid, m - 1, n - 1, memo);
};

算法可视化面板

至此，本题就算是解决了，时间复杂度和空间复杂度都是 $O(MN)$ ，标准的自顶向下动态规划解法。

有的读者可能问，能不能用自底向上的迭代解法来做这道题呢？完全可以的。

首先，类似刚才的 dp 函数，我们需要一个二维 dp 数组，定义如下：

从左上角位置 (0, 0) 走到位置 (i, j) 的最小路径和为 dp[i][j]。

状态转移方程当然不会变的，dp[i][j] 依然取决于 dp[i-1][j] 和 dp[i][j-1]，直接看代码吧：

java

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];

        // **** base case ****
        dp[0][0] = grid[0][0];

        for (int i = 1; i < m; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        
        for (int j = 1; j < n; j++)
            dp[0][j] = dp[0][j - 1] + grid[0][j];        
        // *******************
        
        // 状态转移
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }
}

cpp

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));

        // **** base case ****
        dp[0][0] = grid[0][0];

        for (int i = 1; i < m; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        
        for (int j = 1; j < n; j++)
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        // *******************

        // 状态转移
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }
};

python

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        dp = [[0] * n for _ in range(m)]

        # **** base case ****
        dp[0][0] = grid[0][0]

        for i in range(1, m):
            dp[i][0] = dp[i - 1][0] + grid[i][0]
        
        for j in range(1, n):
            dp[0][j] = dp[0][j - 1] + grid[0][j]        
        # *******************
        
        # 状态转移
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j]

        return dp[m - 1][n - 1]

func minPathSum(grid [][]int) int {
	m := len(grid)
	n := len(grid[0])
	dp := make([][]int, m)
	for i := range dp {
		dp[i] = make([]int, n)
	}

	// **** base case ****
	dp[0][0] = grid[0][0]

	for i := 1; i < m; i++ {
		dp[i][0] = dp[i-1][0] + grid[i][0]
	}

	for j := 1; j < n; j++ {
		dp[0][j] = dp[0][j-1] + grid[0][j]
	}
	// *******************

	// 状态转移
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			dp[i][j] = min(
				dp[i-1][j],
				dp[i][j-1],
			) + grid[i][j]
		}
	}

	return dp[m-1][n-1]
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

javascript

var minPathSum = function(grid) {
    var m = grid.length;
    var n = grid[0].length;
    var dp = new Array(m).fill(0).map(() => new Array(n).fill(0));

    // **** base case ****
    dp[0][0] = grid[0][0];

    for (let i = 1; i < m; i++)
        dp[i][0] = dp[i - 1][0] + grid[i][0];
    
    for (let j = 1; j < n; j++)
        dp[0][j] = dp[0][j - 1] + grid[0][j];        
    // *******************
    
    // 状态转移
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            dp[i][j] = Math.min(
                dp[i - 1][j],
                dp[i][j - 1]
            ) + grid[i][j];
        }
    }

    return dp[m - 1][n - 1];
};

这个解法的 base case 看起来和递归解法略有不同，但实际上是一样的。

因为状态转移为下面这段代码：

dp[i][j] = Math.min(
    dp[i - 1][j],
    dp[i][j - 1]
) + grid[i][j];

那如果 i 或者 j 等于 0 的时候，就会出现索引越界的错误。

所以我们需要提前计算出 dp[0][..] 和 dp[..][0]，然后让 i 和 j 的值从 1 开始迭代。

dp[0][..] 和 dp[..][0] 的值怎么算呢？其实很简单，第一行和第一列的路径和只有下面这一种情况嘛：

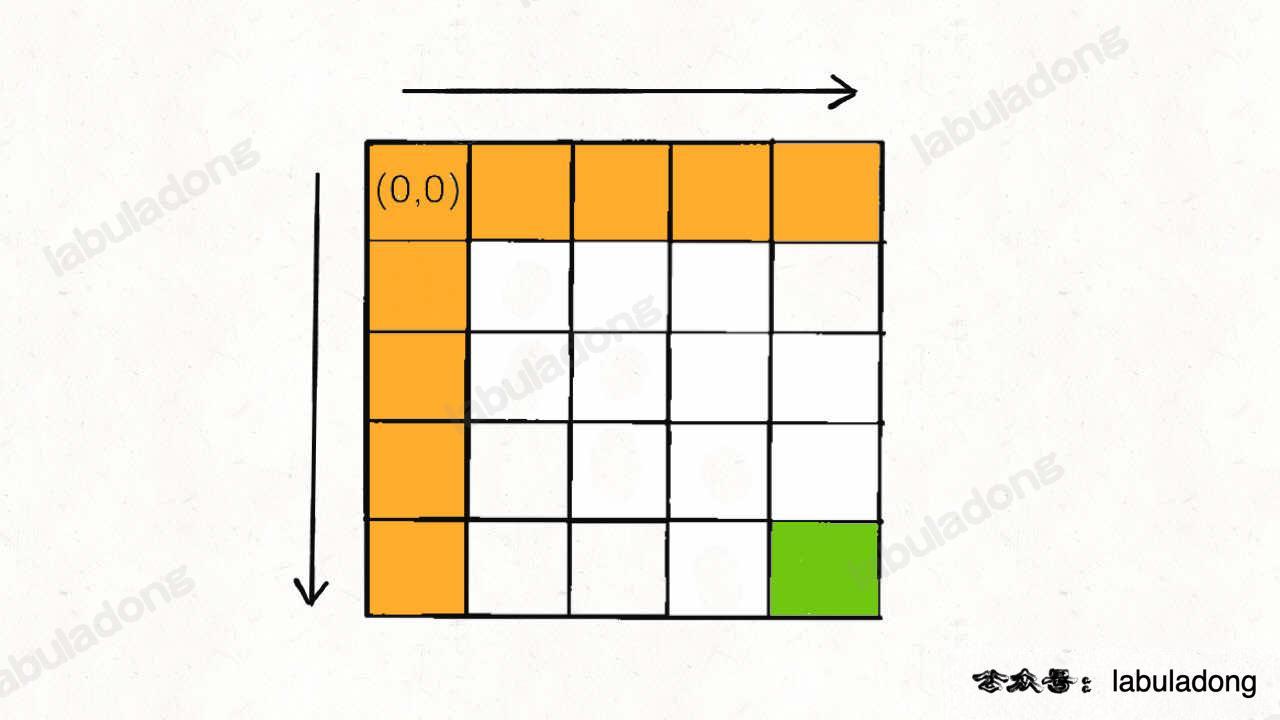
那么按照 dp 数组的定义，dp[i][0] = sum(grid[0..i][0]), dp[0][j] = sum(grid[0][0..j])，也就是如下代码：

// **** base case ****
dp[0][0] = grid[0][0];

for (int i = 1; i < m; i++)
    dp[i][0] = dp[i - 1][0] + grid[i][0];

for (int j = 1; j < n; j++)
    dp[0][j] = dp[0][j - 1] + grid[0][j];        
// *******************

到这里，自底向上的迭代解法也搞定了，那有的读者可能又要问了，能不能优化一下算法的空间复杂度呢？

前文动态规划的降维打击：空间压缩说过降低 dp 数组的技巧，这里也是适用的，不过略微复杂些，本文由于篇幅所限就不写了，有兴趣的读者可以自己尝试一下。

本文到此结束，下篇文章写一道进阶题目，更加巧妙和有趣，敬请期待~

动态规划之最小路径和

64. 最小路径和 https://leetcode.cn/problems/minimum-path-sum