动态规划帮我通关了《辐射4》

本文的封面图是一款叫做《辐射4》的游戏中的一个任务剧情画面：

这个可以转动的圆盘类似是一个密码机关，中间偏上的位置有个红色的指针看到没，你只要转动圆盘可以让指针指向不同的字母，然后再按下中间的按钮就可以输入指针指向的字母。

只要转动圆环，让指针依次指向 R、A、I、L、R、O、A、D 并依次按下按钮，就可以触发机关，打开旁边的门。

至于密码为什么是这几个字母，在游戏中的剧情有暗示，这里就不多说了。

那么这个游戏场景和动态规划有什么关系呢？

我们来没事儿找事儿地想一想，拨动圆盘输入这些字母还挺麻烦的，按照什么顺序才能使得拨动圆盘所需的操作次数最少呢？

拨动圆盘的不同方法所需的操作次数肯定是不同的。

比如说你想把一个字母对准到指针上，你可以顺时针转圆盘，也可以逆时针转圆盘；而且某些字母可能不止出现一次，比如上图中大写字母 O 就在圆盘的不同位置出现了三次，你到时候应该拨哪个 O 才能使得整体的操作次数最少呢？

我们之前也多次说过，遇到求最值的问题，基本都是由动态规划算法来解决，因为动态规划本身就是运筹优化算法的一种嘛。

力扣上就有一道这个转盘游戏的算法题，难度还是 Hard，但我当时看了一眼就做出来了，因为我以前思考过生活中一个非常有意思的例子可以类比到这个问题，下面来简单介绍一下。

我曾经练习过李斯特和肖邦的几首钢琴曲，没练过钢琴的读者可能不知道，练习钢琴曲谱是需要提前确定「指法」的。

五线谱的音符七上八下的，两个手的手指必须互相配合，也就是说你必须确定好每个音符用哪只手的哪个手指来弹奏，写到谱子上。

比如说我很喜欢的一首曲子叫做《爱之梦》，这是我初学时的谱子：

音符上的数字 1 代表用大拇指，2 代表用食指，以此类推。按照确定下来的指法不断练习，形成肌肉记忆，就算是练会一首曲子了。

指法这东西因人而异，比如手大的人可以让中指跨到大拇指的左边，手小的人可能就有些别扭，那同一段谱子对应的指法可能就不一样。

那么问题来了，我应该如何设计指法，才能最小化手指切换的「别扭程度」，也就是最大化演奏的流畅度呢？

这里我就借助了动态规划算法技巧：手指的切换不就是状态的转移么？参考前文 动态规划套路详解，只要明确「状态」和「选择」就可以解决这个问题。

状态是什么？状态就是「下一个需要弹奏的音符」和「当前的手的状态」。

下一个需要弹奏的音符，无非就是钢琴上 88 个琴键中的一个；手的状态也很简单，五个手指头，每个手指头要么按下去了要么没按下去，2 的 5 次方 32 种情况，5 个二进制位就可以表示。

选择是什么？选择就是「下一个音符应该由哪个手指头来弹」，无非就是穷举五个手指头。

当然，结合当前手的状态，做出每个选择需要对应代价的，刚才说过这个代价是因人而异的，所以我需要给自己定制一个损失函数，计算不同指法切换的「别扭程度」。

现在的问题就变成了一个标准的动态规划问题，根据损失函数做出「别扭程度」最小的选择，使得整段演奏最流畅……

当然，最后这个算法时间复杂度太高了，我们刚才分析的只是单个的音符，但如果串成曲子，时空复杂度还得再乘曲子的音符数，很大。

而且，这个损失函数很难量化，钢琴的黑白键命中难度不同，而且「别扭程度」只能靠感觉，有点不严谨……

不过，本就没必要计算整首曲子的指法，只需要计算某些复杂段落的指法即可，这个算法还是比较有效的。

扯了这么多题外话终于要步入正题了，今天要讲的力扣第 514 题「自由之路」和钢琴指法问题有异曲同工之妙，如果你能理解钢琴的例子，相信你也能很快做出这道算法题。

题目给你输入一个字符串 ring 代表圆盘上的字符（指针位置在 12 点钟方向，初始指向 ring[0]），再输入一个字符串 key 代表你需要拨动圆盘输入的字符串，你的算法需要返回输入这个 key 至少进行多少次操作（拨动一格圆盘和按下圆盘中间的按钮都算是一次操作）。

函数签名如下：

int findRotateSteps(String ring, String key);

int findRotateSteps(string ring, string key);

def findRotateSteps(ring: str, key: str) -> int:

func findRotateSteps(ring string, key string) int {}

var findRotateSteps = function(ring, key) {}

比如题目举的例子，输入 ring = "godding", key = "gd"，对应的圆盘如下（大写只是为了清晰，实际上输入的字符串都是小写字母）：

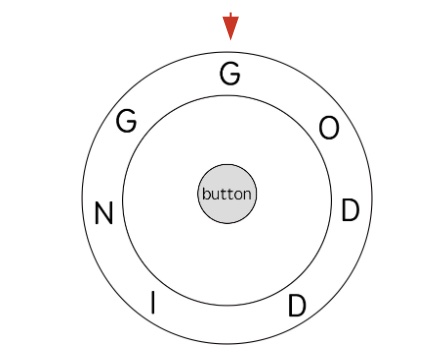
我们需要输入 key = "gd"，算法返回 4。

因为现在指针指的字母就是字母 "g"，所以可以直接按下中间的按钮，然后再将圆盘逆时针拨动两格，让指针指向字母 "d"，然后再按一次中间的按钮。

上述过程，按了两次按钮，拨了两格转盘，总共操作了 4 次，是最少的操作次数，所以算法应该返回 4。

我们这里可以首先给题目做一个等价，转动圆盘是不是就等于拨动指针？

原题可以转化为：圆盘固定，我们可以拨动指针；现在需要我们拨动指针并按下按钮，以最少的操作次数输入 key 对应的字符串。

那么，这个问题如何使用动态规划的技巧解决呢？或者说，这道题的「状态」和「选择」是什么呢？

「状态」就是「当前需要输入的字符」和「当前圆盘指针的位置」。

再具体点，「状态」就是 i 和 j 两个变量。我们可以用 i 表示当前圆盘上指针指向的字符（也就是 ring[i]）；用 j 表示需要输入的字符（也就是 key[j]）。

这样我们可以写这样一个 dp 函数：

int dp(String ring, int i, String key, int j);

int dp(string ring, int i, string key, int j);

def dp(ring: str, i: int, key: str, j: int) -> int:

func dp(ring string, i int, key string, j int) int

var dp = function(ring, i, key, j){}

这个 dp 函数的定义如下：

当圆盘指针指向 ring[i] 时，输入字符串 key[j..] 至少需要 dp(ring, i, key, j) 次操作。

根据这个定义，题目其实就是想计算 dp(ring, 0, key, 0) 的值，而且我们可以把 dp 函数的 base case 写出来：

int dp(String ring, int i, String key, int j) {
    // base case，完成输入
    if (j == key.length()) return 0;
    // ...
}

int dp(string ring, int i, string key, int j) {
    // base case，完成输入
    if (j == key.length()) return 0;
    // ...
}

def dp(ring: str, i: int, key: str, j: int) -> int:
    # base case，完成输入
    if j == len(key):
        return 0
    # ...

func dp(ring string, i int, key string, j int) int {
    // base case，完成输入
    if j == len(key) {
        return 0
    }
    // ...
}

var dp = function(ring, i, key, j) {
    // base case，完成输入
    if (j === key.length) return 0;
    // ...
};

接下来，思考一下如何根据状态做选择，如何进行状态转移？

「选择」就是「如何拨动指针得到待输入的字符」。

再具体点就是，对于现在想输入的字符 key[j]，我们可以如何拨动圆盘，得到这个字符？

比如说输入 ring = "gdonidg"，现在圆盘的状态如下图：

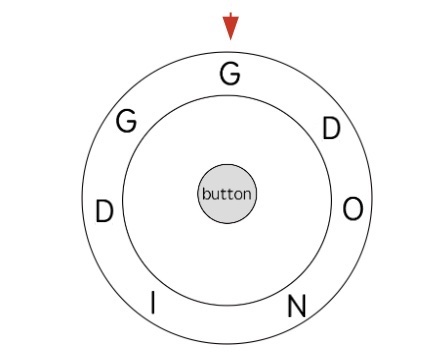
假设我想输入的字符 key[j] = "d"，圆盘中有两个字母 "d"，而且我可以顺时针也可以逆时针拨动指针，所以总共有四种「选择」输入字符 "d"，我们需要选择操作次数最少的那个拨法。

大致的代码逻辑如下：

int dp(String ring, int i, String key, int j) {
    // base case 完成输入
    if (j == key.length()) return 0;
    
    // 做选择
    int res = Integer.MAX_VALUE;
    for (int k : [字符 key[j] 在 ring 中的所有索引]) {
        res = min(
            把 i 顺时针转到 k 的代价,
            把 i 逆时针转到 k 的代价
        );
    }
    
    return res;
}

int dp(string ring, int i, string key, int j) {
    // base case 完成输入
    if (j == key.length()) return 0;
    
    // 做选择
    int res = INT_MAX;
    for (int k : [字符 key[j] 在 ring 中的所有索引]) {
        res = min(
            把 i 顺时针转到 k 的代价,
            把 i 逆时针转到 k 的代价
        );
    }

    return res;
}

def dp(ring: str, i: int, key: str, j: int) -> int:
    # base case 完成输入
    if j == len(key): return 0
    
    # 做选择
    res = float('inf')
    for k in [字符 key[j] 在 ring 中的所有索引]:
        res = min(
            转到 k 顺时针的代价,
            转到 k 逆时针的代价
        )
    
    return res

func dp(ring string, i int, key string, j int) int {
    // base case 完成输入
    if j == len(key) {
        return 0
    }
    
    // 做选择
    res := math.MaxInt64
    for _, k := range [字符 key[j] 在 ring 中的所有索引] {
        res = min(
            转到 k 顺时针的代价,
            转到 k 逆时针的代价
        )
    }

    return res
}

var dp = function(ring, i, key, j) {
    // base case 完成输入
    if (j === key.length) return 0;
    
    // 做选择
    var res = Infinity;
    for (var k of [字符 key[j] 在 ring 中的所有索引]) {
        res = Math.min(
            把 i 顺时针转到 k 的代价,
            把 i 逆时针转到 k 的代价
        );
    }
    
    return res;
}

至于到底是顺时针还是逆时针，其实非常好判断，怎么近就怎么来；但是对于圆盘中的两个字符 "d"，还能是怎么近怎么来吗？

不能，因为这和 key[i] 之后需要输入的字符有关，还是上面的例子：

如果输入的是 key = "di"，那么即便右边的 "d" 离得近，也应该去左边的 "d"，因为左边的 "d" 旁边就是 "i"，「整体」的操作数最少。

那么，应该如何判断呢？其实就是穷举，递归调用 dp 函数，把两种选择的「整体」代价算出来，然后再做比较就行了。

讲到这就差不多了，直接看最终代码吧：

class Solution {
    // 字符 -> 索引列表
    HashMap<Character, List<Integer>> charToIndex = new HashMap<>();
    // 备忘录
    int[][] memo;

    // 主函数
    public int findRotateSteps(String ring, String key) {
        int m = ring.length();
        int n = key.length();
        // 备忘录全部初始化为 0
        memo = new int[m][n];
        // 记录圆环上字符到索引的映射
        for (int i = 0; i < ring.length(); i++) {
            char c = ring.charAt(i);
            if (!charToIndex.containsKey(c)) {
                charToIndex.put(c, new LinkedList<>());
            }
            charToIndex.get(c).add(i);
        }
        // 圆盘指针最初指向 12 点钟方向，
        // 从第一个字符开始输入 key
        return dp(ring, 0, key, 0);
    }

    // 计算圆盘指针在 ring[i]，输入 key[j..] 的最少操作数
    int dp(String ring, int i, String key, int j) {
        // base case 完成输入
        if (j == key.length()) return 0;
        // 查找备忘录，避免重叠子问题
        if (memo[i][j] != 0) return memo[i][j];
        
        int n = ring.length();
        // 做选择
        int res = Integer.MAX_VALUE;
        // ring 上可能有多个字符 key[j]
        for (int k : charToIndex.get(key.charAt(j))) {
            // 拨动指针的次数
            int delta = Math.abs(k - i);
            // 选择顺时针还是逆时针
            delta = Math.min(delta, n - delta);
            // 将指针拨到 ring[k]，继续输入 key[j+1..]
            int subProblem = dp(ring, k, key, j + 1);
            // 选择「整体」操作次数最少的
            // 加一是因为按动按钮也是一次操作
            res = Math.min(res, 1 + delta + subProblem);
        }
        // 将结果存入备忘录
        memo[i][j] = res;
        return res;
    }
}

class Solution {
    // 字符 -> 索引列表
    unordered_map<char, vector<int>> charToIndex;
    // 备忘录
    vector<vector<int>> memo;

    // 主函数
public:
    int findRotateSteps(string ring, string key) {
        int m = ring.size();
        int n = key.size();
        // 备忘录全部初始化为 0
        memo = vector<vector<int>>(m, vector<int>(n, 0));
        // 记录圆环上字符到索引的映射
        for (int i = 0; i < ring.size(); i++) {
            char c = ring[i];
            if (!charToIndex.count(c)) {
                charToIndex[c] = vector<int>();
            }
            charToIndex[c].push_back(i);
        }
        // 圆盘指针最初指向 12 点钟方向，
        // 从第一个字符开始输入 key
        return dp(ring, 0, key, 0);
    }

private:
    // 计算圆盘指针在 ring[i]，输入 key[j..] 的最少操作数
    int dp(const string& ring, int i, const string& key, int j) {
        // base case 完成输入
        if (j == key.size()) return 0;
        // 查找备忘录，避免重叠子问题
        if (memo[i][j] != 0) return memo[i][j];
        
        int n = ring.size();
        // 做选择
        int res = INT_MAX;
        // ring 上可能有多个字符 key[j]
        for (int k : charToIndex[key[j]]) {
            // 拨动指针的次数
            int delta = abs(k - i);
            // 选择顺时针还是逆时针
            delta = min(delta, n - delta);
            // 将指针拨到 ring[k]，继续输入 key[j+1..]
            int subProblem = dp(ring, k, key, j + 1);
            // 选择「整体」操作次数最少的
            // 加一是因为按动按钮也是一次操作
            res = min(res, 1 + delta + subProblem);
        }
        // 将结果存入备忘录
        memo[i][j] = res;
        return res;
    }
};

class Solution:
    def __init__(self):
        # 字符 -> 索引列表
        self.charToIndex = collections.defaultdict(list)
        # 备忘录
        self.memo = None

    # 主函数
    def findRotateSteps(self, ring: str, key: str) -> int:
        m = len(ring)
        n = len(key)
        # 备忘录全部初始化为 0
        self.memo = [[0] * n for _ in range(m)]
        # 记录圆环上字符到索引的映射
        for i, c in enumerate(ring):
            self.charToIndex[c].append(i)
        # 圆盘指针最初指向 12 点钟方向，
        # 从第一个字符开始输入 key
        return self.dp(ring, 0, key, 0)
    
    # 计算圆盘指针在 ring[i]，输入 key[j..] 的最少操作数
    def dp(self, ring: str, i: int, key: str, j: int) -> int:
        # base case 完成输入
        if j == len(key):
            return 0
        # 查找备忘录，避免重叠子问题
        if self.memo[i][j] != 0:
            return self.memo[i][j]
        
        n = len(ring)
        # 做选择
        res = float('inf')
        # ring 上可能有多个字符 key[j]
        for k in self.charToIndex[key[j]]:
            # 拨动指针的次数
            delta = abs(k - i)
            # 选择顺时针还是逆时针
            delta = min(delta, n - delta)
            # 将指针拨到 ring[k]，继续输入 key[j+1..]
            subProblem = self.dp(ring, k, key, j + 1)
            # 选择「整体」操作次数最少的
            # 加一是因为按动按钮也是一次操作
            res = min(res, 1 + delta + subProblem)
        # 将结果存入备忘录
        self.memo[i][j] = res
        return res

// 主函数
func findRotateSteps(ring string, key string) int {
	m := len(ring)
	n := len(key)
	// 初始化备忘录
	memo := make([][]int, m)
	for i := range memo {
		memo[i] = make([]int, n)
	}
	// 初始化字符到索引的映射
	charToIndex := make(map[rune][]int)
	for i, c := range ring {
		charToIndex[c] = append(charToIndex[c], i)
	}

	var dp func(ring string, i int, key string, j int, memo [][]int, charToIndex map[rune][]int) int
	dp = func(ring string, i int, key string, j int, memo [][]int, charToIndex map[rune][]int) int {
		// base case 完成输入
		if j == len(key) {
			return 0
		}
		// 查找备忘录，避免重叠子问题
		if memo[i][j] != 0 {
			return memo[i][j]
		}
		
		n := len(ring)
		// 做选择
		res := math.MaxInt32
		// ring 上可能有多个字符 key[j]
		for _, k := range charToIndex[rune(key[j])] {
			// 拨动指针的次数
			delta := int(math.Abs(float64(k - i)))
			// 选择顺时针还是逆时针
			delta = min(delta, n - delta)
			// 将指针拨到 ring[k]，继续输入 key[j+1..]
			subProblem := dp(ring, k, key, j + 1, memo, charToIndex)
			// 选择「整体」操作次数最少的
			// 加一是因为按动按钮也是一次操作
			res = min(res, 1 + delta + subProblem)
		}
		// 将结果存入备忘录
		memo[i][j] = res
		return res
	}

	// 圆盘指针最初指向 12 点钟方向，
	// 从第一个字符开始输入 key
	return dp(ring, 0, key, 0, memo, charToIndex)
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

var findRotateSteps = function(ring, key) {
    // 字符 -> 索引列表
    let charToIndex = new Map();
    // 备忘录
    let memo;

    // 主函数
    function main(ring, key) {
        let m = ring.length;
        let n = key.length;
        // 备忘录全部初始化为 0
        memo = Array.from({ length: m }, () => Array(n).fill(0));
        // 记录圆环上字符到索引的映射
        for (let i = 0; i < ring.length; i++) {
            let c = ring.charAt(i);
            if (!charToIndex.has(c)) {
                charToIndex.set(c, []);
            }
            charToIndex.get(c).push(i);
        }
        // 圆盘指针最初指向 12 点钟方向，
        // 从第一个字符开始输入 key
        return dp(ring, 0, key, 0);
    }

    // 计算圆盘指针在 ring[i]，输入 key[j..] 的最少操作数
    function dp(ring, i, key, j) {
        // base case 完成输入
        if (j == key.length) return 0;
        // 查找备忘录，避免重叠子问题
        if (memo[i][j] != 0) return memo[i][j];
        
        let n = ring.length;
        // 做选择
        let res = Infinity;
        // ring 上可能有多个字符 key[j]
        for (let k of charToIndex.get(key.charAt(j))) {
            // 拨动指针的次数
            let delta = Math.abs(k - i);
            // 选择顺时针还是逆时针
            delta = Math.min(delta, n - delta);
            // 将指针拨到 ring[k]，继续输入 key[j+1..]
            let subProblem = dp(ring, k, key, j + 1);
            // 选择「整体」操作次数最少的
            // 加一是因为按动按钮也是一次操作
            res = Math.min(res, 1 + delta + subProblem);
        }
        // 将结果存入备忘录
        memo[i][j] = res;
        return res;
    }

    return main(ring, key);
};