Union-Find 并查集算法
原创约 4176 字
本文讲解的例题
并查集（Union-Find）算法是一个专门针对「动态连通性」的算法，我之前写过两次，因为这个算法的考察频率高，而且它也是最小生成树算法的前置知识，所以我整合了本文，争取一篇文章把这个算法讲明白。
首先，从什么是图的动态连通性开始讲。
一、动态连通性
简单说，动态连通性其实可以抽象成给一幅图连线。比如下面这幅图，总共有 10 个节点，他们互不相连，分别用 0~9 标记：
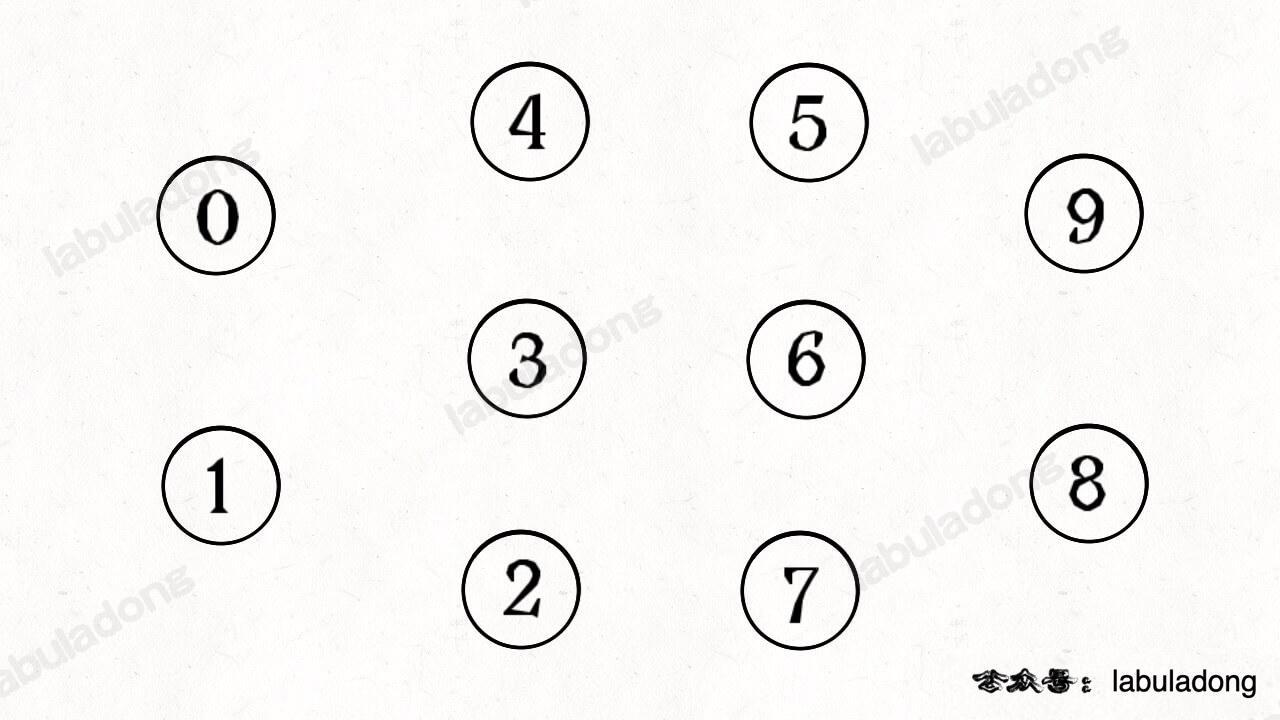
现在我们的 Union-Find 算法主要需要实现这两个 API：
java 🟢
class UF {
// 将 p 和 q 连接
public void union(int p, int q);
// 判断 p 和 q 是否连通
public boolean connected(int p, int q);
// 返回图中有多少个连通分量
public int count();
}cpp 🤖
class UF {
public:
// 将 p 和 q 连接
void union_(int p, int q) = 0;
// 判断 p 和 q 是否连通
bool connected(int p, int q) = 0;
// 返回图中有多少个连通分量
int count() = 0;
};python 🤖
class UF:
# 将 p 和 q 连接
def union(self, p, q):
pass
# 判断 p 和 q 是否连通
def connected(self, p, q):
pass
# 返回图中有多少个连通分量
def count(self):
passgo 🤖
type UF struct{}
// 将 p 和 q 连接
func (uf *UF) Union(p int, q int) {}
// 判断 p 和 q 是否连通
func (uf *UF) Connected(p int, q int) bool {
return false
}
// 返回图中有多少个连通分量
func (uf *UF) Count() int {
return 0
}javascript 🤖
var UF = function() {
// 将 p 和 q 连接
this.union = function(p, q) {};
// 判断 p 和 q 是否连通
this.connected = function(p, q) {};
// 返回图中有多少个连通分量
this.count = function() {};
};这里所说的「连通」是一种等价关系，也就是说具有如下三个性质：
1、自反性：节点 p 和 p 是连通的。
2、对称性：如果节点 p 和 q 连通，那么 q 和 p 也连通。
3、传递性：如果节点 p 和 q 连通，q 和 r 连通，那么 p 和 r 也连通。
比如说之前那幅图，0～9 任意两个不同的点都不连通，调用 connected 都会返回 false，连通分量为 10 个。
如果现在调用 union(0, 1)，那么 0 和 1 被连通，连通分量降为 9 个。
再调用 union(1, 2)，这时 0,1,2 都被连通，调用 connected(0, 2) 也会返回 true，连通分量变为 8 个。
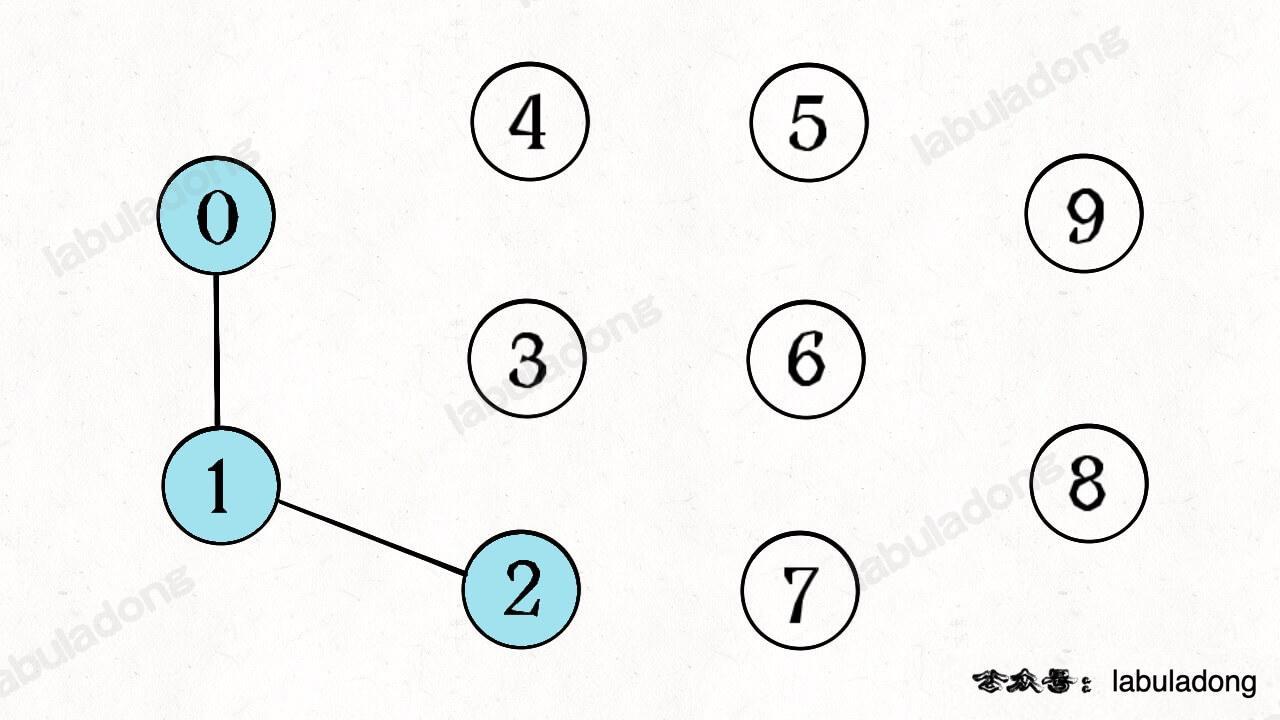
判断这种「等价关系」非常实用，比如说编译器判断同一个变量的不同引用，比如社交网络中的朋友圈计算等等。
这样，你应该大概明白什么是动态连通性了，Union-Find 算法的关键就在于 union 和 connected 函数的效率。那么用什么模型来表示这幅图的连通状态呢？用什么数据结构来实现代码呢？