跳至主要內容

二叉树心法（序列化篇）

labuladong原创约 5333 字

297. 二叉树的序列化与反序列化 https://leetcode.cn/problems/serialize-and-deserialize-binary-tree

297. Serialize and Deserialize Binary Tree https://leetcode.com/problems/serialize-and-deserialize-binary-tree

本文讲解的例题

LeetCode力扣难度
297. Serialize and Deserialize Binary Tree297. 二叉树的序列化与反序列化🔴

前置知识

阅读本文前，你需要先学习：

本文是承接 二叉树心法（纲领篇） 的第三篇文章，前文 二叉树心法（构造篇） 带你学习了二叉树构造技巧，本文加大难度，让你对二叉树同时进行「序列化」和「反序列化」。

要说序列化和反序列化，得先从 JSON 数据格式说起。

JSON 的运用非常广泛，比如我们经常将编程语言中的结构体序列化成 JSON 字符串，存入缓存或者通过网络发送给远端服务，消费者接受 JSON 字符串然后进行反序列化，就可以得到原始数据了。

这就是序列化和反序列化的目的，以某种特定格式组织数据，使得数据可以独立于编程语言。

那么假设现在有一棵用 Java 实现的二叉树，我想把它通过某些方式存储下来，然后用 C++ 读取这棵并还原这棵二叉树的结构，怎么办？这就需要对二叉树进行序列化和反序列化了。

零、前/中/后序和二叉树的唯一性

谈具体的题目之前，我们先思考一个问题：什么样的序列化的数据可以反序列化出唯一的一棵二叉树？

比如说，如果给你一棵二叉树的前序遍历结果，你是否能够根据这个结果还原出这棵二叉树呢？

答案是也许可以，也许不可以，具体要看你给的前序遍历结果是否包含空指针的信息。如果包含了空指针，那么就可以唯一确定一棵二叉树，否则就不行。

举例来说，如果我给你这样一个不包含空指针的前序遍历结果 [1,2,3,4,5]，那么如下两棵二叉树都是满足这个前序遍历结果的：

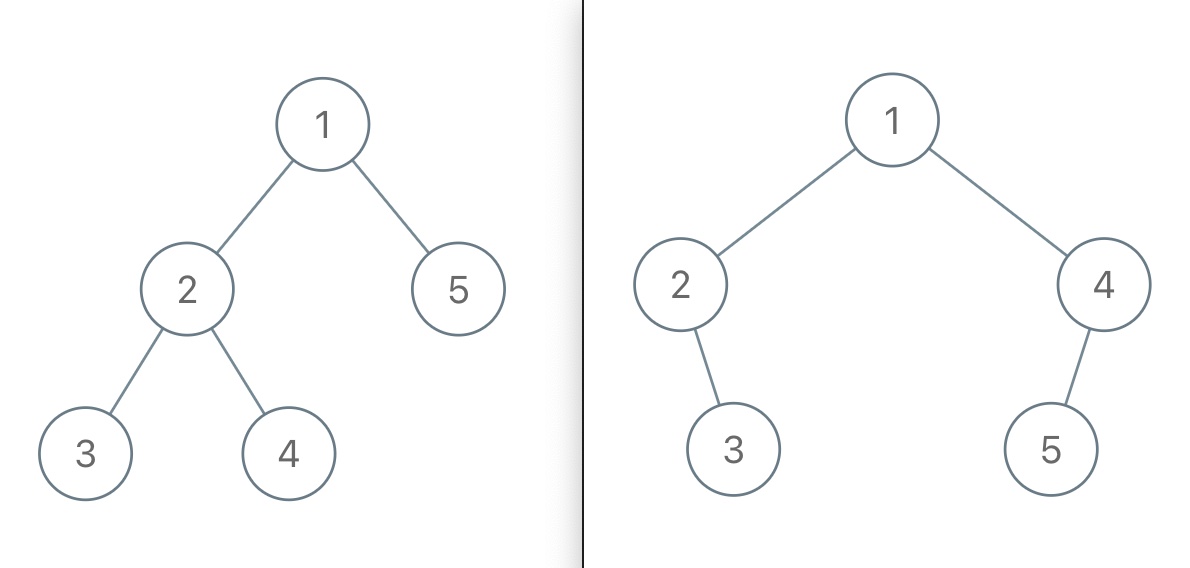
所以给定不包含空指针信息的前序遍历结果，是不能还原出唯一的一棵二叉树的。

但如果我的前序遍历结果包含空指针的信息，那么就能还原出唯一的一棵二叉树了。比如说用 # 表示空指针，上图左侧的二叉树的前序遍历结果就是 [1,2,3,#,#,4,#,#,5,#,#]，上图右侧的二叉树的前序遍历结果就是 [1,2,#,3,#,#,4,5,#,#,#]，它俩就区分开了。

那么估计就有聪明的小伙伴说了：二叉树心法了。

首先要夸一下这种举一反三的思维，但很不幸，正确答案是，即便你包含了空指针的信息，也只有前序和后序的遍历结果才能唯一还原二叉树，中序遍历结果做不到。

本文后面会具体探讨这个问题，这里只简单说下原因：因为前序/后序遍历的结果中，可以确定根节点的位置，而中序遍历的结果中，根节点的位置是无法确定的。

更直观的，比如如下两棵二叉树显然拥有不同的结构，但它俩的中序遍历结果都是 [#,1,#,1,#]，无法区分：

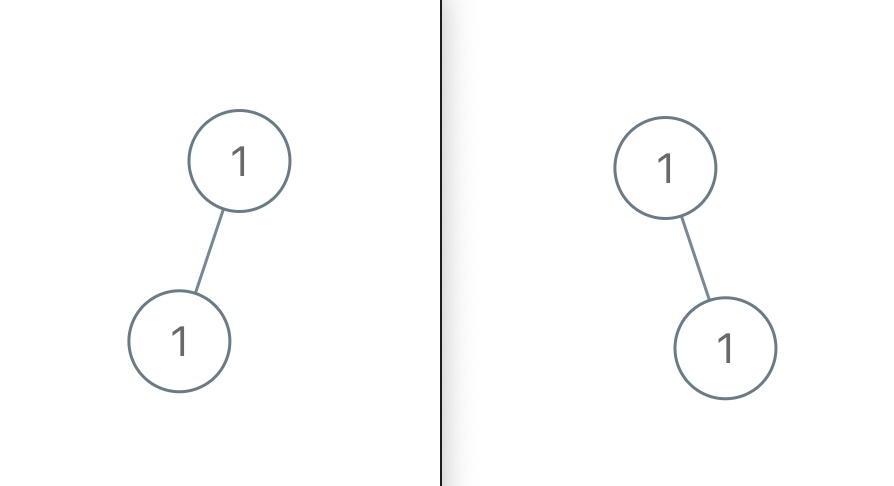
说了这么多，总结下结论，当二叉树中节点的值不存在重复时：

  1. 如果你的序列化结果中不包含空指针的信息，且你只给出一种遍历顺序，那么你无法还原出唯一的一棵二叉树。

  2. 如果你的序列化结果中不包含空指针的信息，且你会给出两种遍历顺序，那么按照前文 二叉树心法（构造篇） 所说，分两种情况：

    2.1. 如果你给出的是前序和中序，或者后序和中序，那么你可以还原出唯一的一棵二叉树。

    2.2. 如果你给出前序和后序，那么你无法还原出唯一的一棵二叉树。

  3. 如果你的序列化结果中包含空指针的信息，且你只给出一种遍历顺序，也要分两种情况：

    3.1. 如果你给出的是前序或者后序，那么你可以还原出唯一的一棵二叉树。

    3.2. 如果你给出的是中序，那么你无法还原出唯一的一棵二叉树。

我在开头提一下这些总结性的认识，可以理解性记忆，之后会遇到一些相关的题目，再回过头来看看这些总结，会有更深的理解，下面看具体的题目吧。

一、题目描述

力扣第 297 题「二叉树的序列化与反序列化」就是给你输入一棵二叉树的根节点 root，要求你实现如下一个类：

java 🟢
public class Codec {

    // 把一棵二叉树序列化成字符串
    public String serialize(TreeNode root) {}

    // 把字符串反序列化成二叉树
    public TreeNode deserialize(String data) {}
}

我们可以用 serialize 方法将二叉树序列化成字符串，用 deserialize 方法将序列化的字符串反序列化成二叉树，至于以什么格式序列化和反序列化，这个完全由你决定。

比如说输入如下这样一棵二叉树：

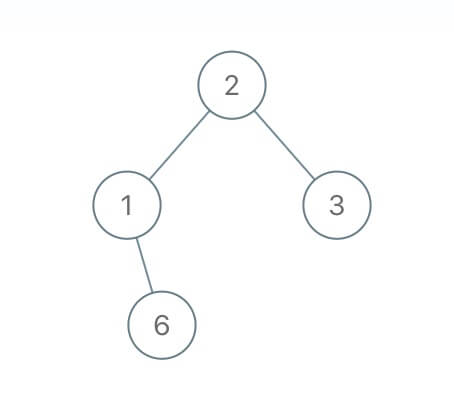
serialize 方法也许会把它序列化成字符串 2,1,#,6,#,#,3,#,#，其中 # 表示 null 指针，那么把这个字符串再输入 deserialize 方法，依然可以还原出这棵二叉树。

也就是说，这两个方法会成对儿使用，你只要保证他俩能够自洽就行了。

想象一下，二叉树是一个二维平面内的结构，而序列化出来的字符串是一个线性的一维结构。所谓的序列化不过就是把结构化的数据「打平」，本质就是在考察二叉树的遍历方式。

二叉树的遍历方式有哪些？递归遍历方式有前序遍历，中序遍历，后序遍历；迭代方式一般是层级遍历。本文就把这些方式都尝试一遍，来实现 serialize 方法和 deserialize 方法。

二、前序遍历解法

前文 二叉树的遍历基础 说过了二叉树的几种遍历方式，前序遍历框架如下：

java 🟢
void traverse(TreeNode root) {
    if (root == null) return;

    // 前序位置的代码
    traverse(root.left);
    traverse(root.right);
}

真的很简单，在递归遍历两棵子树之前写的代码就是前序遍历代码，那么请你看一看如下伪码：

java 🟢
LinkedList<Integer> res;
void traverse(TreeNode root) {
    if (root == null) {
        // 暂且用数字 -1 代表空指针 null
        res.addLast(-1);
        return;
    }

    // ****** 前序位置 ********
    res.addLast(root.val);
    // ***********************

    traverse(root.left);
    traverse(root.right);
}

调用 traverse 函数之后，你是否可以立即想出这个 res 列表中元素的顺序是怎样的？比如如下二叉树（# 代表空指针 null），可以直观看出前序遍历做的事情：

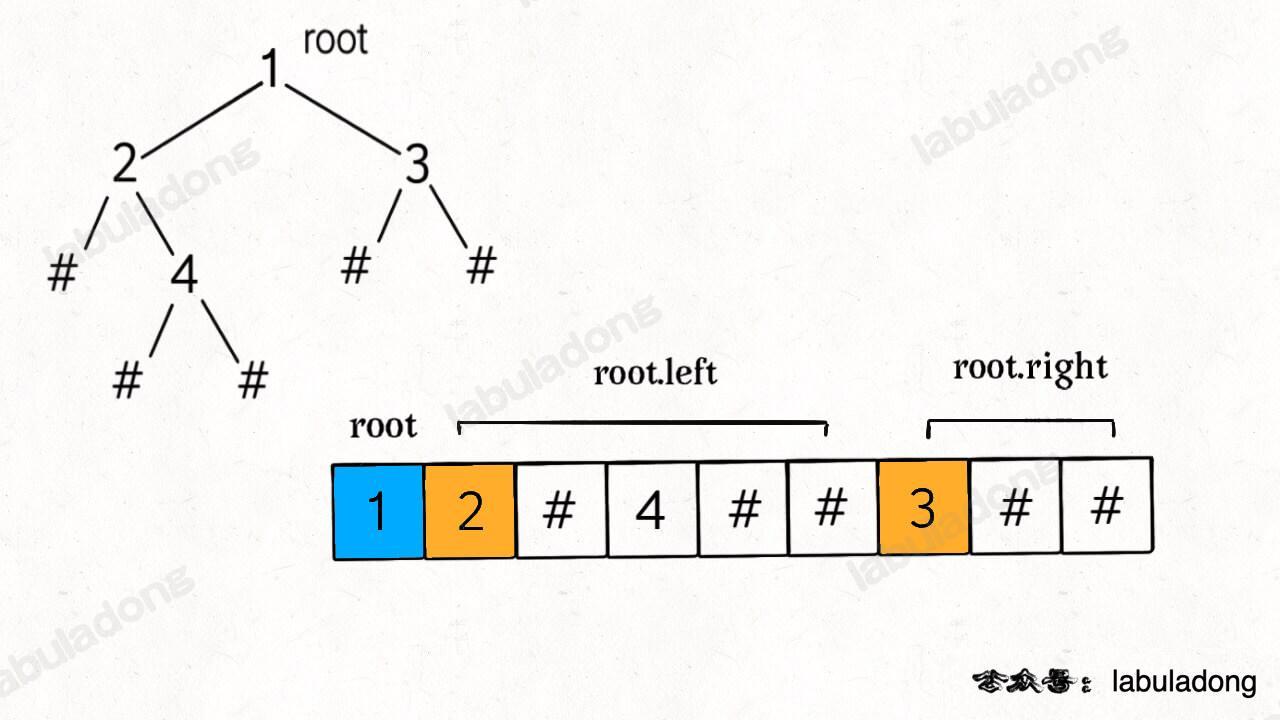
那么 res = [1,2,-1,4,-1,-1,3,-1,-1]，这就是将二叉树「打平」到了一个列表中，其中 -1 代表 null。

那么，将二叉树打平到一个字符串中也是完全一样的：

java 🟢
// 代表分隔符的字符
String SEP = ",";

// 代表 null 空指针的字符
String NULL = "#";

// 用于拼接字符串
StringBuilder sb = new StringBuilder();

// 将二叉树打平为字符串
void traverse(TreeNode root, StringBuilder sb) {
    if (root == null) {
        sb.append(NULL).append(SEP);
        return;
    }

    // ***** 前序位置 *****
    sb.append(root.val).append(SEP);
    // *********************

    traverse(root.left, sb);
    traverse(root.right, sb);
}

StringBuilder 可以用于高效拼接字符串，所以也可以认为是一个列表，用 , 作为分隔符，用 # 表示空指针 null，调用完 traverse 函数后，sb 中的字符串应该是 1,2,#,4,#,#,3,#,#,。

至此，我们已经可以写出序列化函数 serialize 的代码了：

java 🟢
class Codec {
    String SEP = ",";
    String NULL = "#";

    // 主函数，将二叉树序列化为字符串
    public String serialize(TreeNode root) {
        StringBuilder sb = new StringBuilder();
        _serialize(root, sb);
        return sb.toString();
    }

    // 辅助函数，将二叉树存入 StringBuilder
    void _serialize(TreeNode root, StringBuilder sb) {
        if (root == null) {
            sb.append(NULL).append(SEP);
            return;
        }

        // ****** 前序位置 ********
        sb.append(root.val).append(SEP);

        // ***********************

        _serialize(root.left, sb);
        _serialize(root.right, sb);
    }
}

现在，思考一下如何写 deserialize 函数，将字符串反过来构造二叉树。

首先我们可以把字符串转化成列表：

java 🟢
String data = "1,2,#,4,#,#,3,#,#,";
String[] nodes = data.split(",");

这样，nodes 列表就是二叉树的前序遍历结果，问题转化为：如何通过二叉树的前序遍历结果还原一棵二叉树？

提示

前文 二叉树心法（构造篇） 说过，至少要得到前、中、后序遍历中的两种互相配合才能还原二叉树。那是因为前文的遍历结果没有记录空指针的信息。这里的 nodes 列表包含了空指针的信息，所以只使用 nodes 列表就可以还原二叉树。

根据我们刚才的分析，nodes 列表就是一棵打平的二叉树：

那么，反序列化过程也是一样，先确定根节点 root，然后遵循前序遍历的规则，递归生成左右子树即可：

三、后序遍历解法

四、中序遍历解法

五、层级遍历解法

loading...

上次编辑于: 2024/12/6 11:53:39