小而美的算法技巧：前缀和数组

labuladong原创约 1507 字

本文讲解的例题

LeetCode	力扣	难度
303. Range Sum Query - Immutable	303. 区域和检索 - 数组不可变	🟢
304. Range Sum Query 2D - Immutable	304. 二维区域和检索 - 矩阵不可变	🟠

前置知识

阅读本文前，你需要先学习：

前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和。

一维数组中的前缀和

先看一道例题，力扣第 303 题「区域和检索 - 数组不可变」，让你计算数组区间内元素的和，这是一道标准的前缀和问题：

303. 区域和检索 - 数组不可变 | 力扣 | LeetCode |

给定一个整数数组 nums，处理以下类型的多个查询:

计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的和，其中 left <= right

实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

提示：

1 <= nums.length <= 10⁴
-10⁵ <= nums[i] <= 10⁵
0 <= i <= j < nums.length
最多调用 10⁴ 次 sumRange 方法

java 🟢

// 题目要求你实现这样一个类
class NumArray {

    public NumArray(int[] nums) {}
    
    // 查询闭区间 [left, right] 的累加和
    public int sumRange(int left, int right) {}
}

cpp 🤖

// 题目要求你实现这样一个类
class NumArray {
public:
    NumArray(vector<int>& nums) {}
    
    // 查询闭区间 [left, right] 的累加和
    int sumRange(int left, int right) {}
};

python 🤖

# 题目要求你实现这样一个类
class NumArray:
    
    def __init__(self, nums: List[int]):
        pass
        
    # 查询闭区间 [left, right] 的累加和
    def sumRange(self, left: int, right: int) -> int:
        pass

go 🤖

// 题目要求你实现这样一个类
type NumArray struct {}

func Constructor(nums []int) NumArray {}

// 查询闭区间 [left, right] 的累加和
func (this *NumArray) SumRange(left int, right int) int {}

javascript 🤖

// 题目要求你实现这样一个类
var NumArray = function(nums) {
  
  this.nums = nums;
  
  // 查询闭区间 [left, right] 的累加和
  this.sumRange = function(left, right) {}
  
};

sumRange 函数需要计算并返回一个索引区间之内的元素和，没学过前缀和的人可能写出如下代码：

java 🟢

class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    public int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
}

cpp 🤖

class NumArray {
    
private:
    vector<int> nums;

public:
    NumArray(vector<int>& nums) {
        this->nums = nums;
    }
    
    int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
};

python 🤖

class NumArray:
    def __init__(self, nums: List[int]):
        self.nums = nums
    
    def sumRange(self, left: int, right: int) -> int:
        res = 0
        for i in range(left, right+1):
            res += self.nums[i]
        return res

go 🤖

type NumArray struct {
    nums []int
}

func Constructor(nums []int) NumArray {
    return NumArray{nums: nums}
}

func (this *NumArray) SumRange(left int, right int) int {
    res := 0
    for i := left; i <= right; i++{
        res += this.nums[i]
    }
    return res
}

javascript 🤖

var NumArray = function(nums) {
    this.nums = nums;
}

NumArray.prototype.sumRange = function(left, right) {
    let res = 0;
    for (let i = left; i <= right; i++) {
        res += this.nums[i];
    }
    return res;
}

这样，可以达到效果，但是效率很差，因为 sumRange 方法会被频繁调用，而它的最坏时间复杂度是 $O(N)$ ，其中 N 代表 nums 数组的长度。

这道题的最优解法是使用前缀和技巧，将 sumRange 函数的时间复杂度降为 $O(1)$ ，说白了就是不要在 sumRange 里面用 for 循环，咋整？

直接看代码实现：

java 🟢

class NumArray {
    // 前缀和数组
    private int[] preSum;

    // 输入一个数组，构造前缀和
    public NumArray(int[] nums) {
        // preSum[0] = 0，便于计算累加和
        preSum = new int[nums.length + 1];
        // 计算 nums 的累加和
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    // 查询闭区间 [left, right] 的累加和
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

cpp 🤖

class NumArray {
private:
    // 前缀和数组
    vector<int> preSum;

public:
    // 输入一个数组，构造前缀和
    NumArray(vector<int>& nums) {
        // preSum[0] = 0，便于计算累加和
        preSum.resize(nums.size() + 1);
        // 计算 nums 的累加和
        for (int i = 1; i < preSum.size(); i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    // 查询闭区间 [left, right] 的累加和
    int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
};

python 🤖

class NumArray:
    def __init__(self, nums: List[int]):
        # 前缀和数组
        self.preSum = [0] * (len(nums) + 1)
        # 计算 nums 的累加和
        for i in range(1, len(self.preSum)):
            self.preSum[i] = self.preSum[i - 1] + nums[i - 1]

    def sumRange(self, left: int, right: int) -> int:
        # 查询闭区间 [left, right] 的累加和
        return self.preSum[right + 1] - self.preSum[left]

go 🤖

type NumArray struct {
    // 前缀和数组
    preSum []int
}

// 输入一个数组，构造前缀和
func Constructor(nums []int) NumArray {
    // preSum[0] = 0，便于计算累加和
    n := len(nums)
    preSum := make([]int, n + 1)
    // 计算 nums 的累加和
    for i := 1; i < n + 1; i++ {
        preSum[i] = preSum[i - 1] + nums[i - 1]
    }

    return NumArray{preSum: preSum}
}

// 查询闭区间 [left, right] 的累加和
func (this *NumArray) SumRange(left int, right int) int {
    return this.preSum[right + 1] - this.preSum[left]
}

javascript 🤖

var NumArray = function(nums) {
    // 前缀和数组
    this.preSum = new Array(nums.length + 1);
    
    // 计算 nums 的累加和
    this.preSum[0] = 0;
    for (let i = 1; i < this.preSum.length; i++) {
        this.preSum[i] = this.preSum[i - 1] + nums[i - 1];
    }
};

// 查询闭区间 [left, right] 的累加和
NumArray.prototype.sumRange = function(left, right) {
    return this.preSum[right + 1] - this.preSum[left];
};

核心思路是我们 new 一个新的数组 preSum 出来，preSum[i] 记录 nums[0..i-1] 的累加和，看图 10 = 3 + 5 + 2：

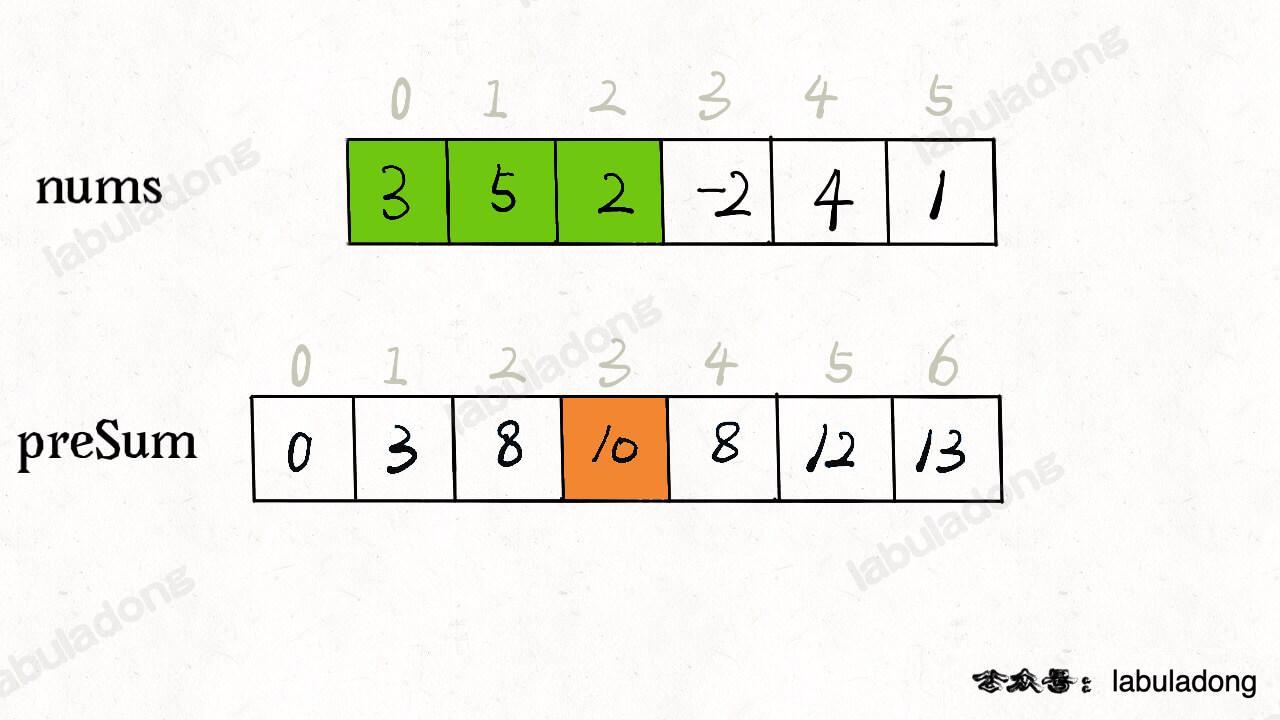
看这个 preSum 数组，如果我想求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。

这样，sumRange 函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数 $O(1)$ 。

这个技巧在生活中运用也挺广泛的，比方说，你们班上有若干同学，每个同学有一个期末考试的成绩（满分 100 分），那么请你实现一个 API，输入任意一个分数段，返回有多少同学的成绩在这个分数段内。

那么，你可以先通过计数排序的方式计算每个分数具体有多少个同学，然后利用前缀和技巧来实现分数段查询的 API：

// 存储着所有同学的分数
int[] scores;
// 试卷满分 100 分
int[] count = new int[100 + 1];
// 记录每个分数有几个同学
for (int score : scores)
    count[score]++;
// 构造前缀和
for (int i = 1; i < count.length; i++)
    count[i] = count[i] + count[i-1];
// 利用 count 这个前缀和数组进行分数段查询

接下来，我们看一看前缀和思路在二维数组中如何运用。

二维矩阵中的前缀和

这是力扣第 304 题「二维区域和检索 - 矩阵不可变」，其实和上一题类似，上一题是让你计算子数组的元素之和，这道题让你计算二维矩阵中子矩阵的元素之和：

304. 二维区域和检索 - 矩阵不可变 | 力扣 | LeetCode |

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

示例 1：

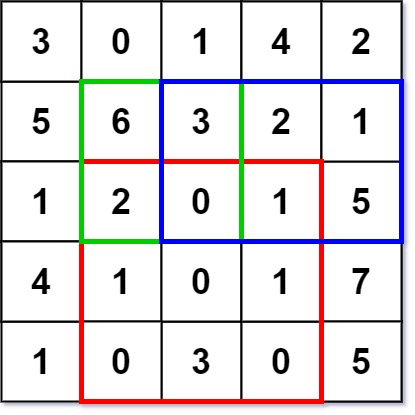
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁵ <= matrix[i][j] <= 10⁵
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 10⁴ 次 sumRegion 方法

当然，你可以用一个嵌套 for 循环去遍历这个矩阵，但这样的话 sumRegion 函数的时间复杂度就高了，你算法的格局就低了。

注意任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算：

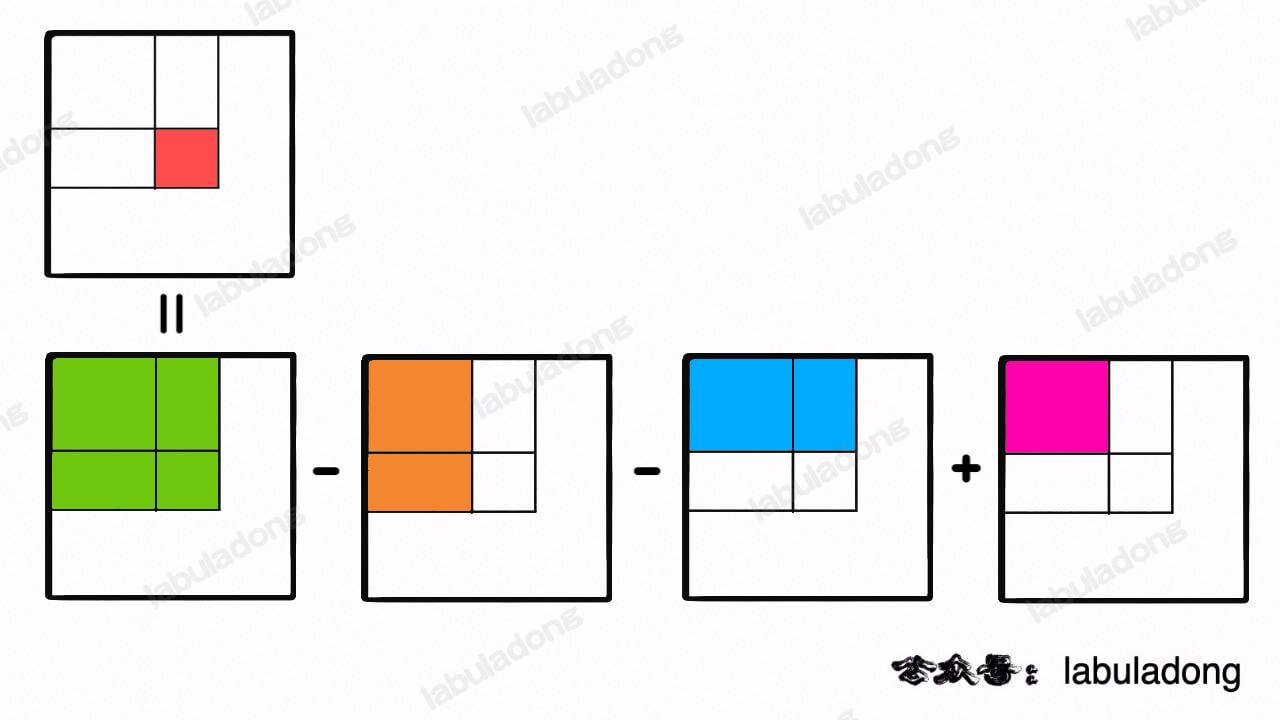
而这四个大矩阵有一个共同的特点，就是左上角都是 (0, 0) 原点。

那么做这道题更好的思路和一维数组中的前缀和是非常类似的，我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和：

java 🟢

class NumMatrix {
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个矩阵 [0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // 计算子矩阵 [x1, y1, x2, y2] 的元素和
    public int sumRegion(int x1, int y1, int x2, int y2) {
        // 目标矩阵之和由四个相邻矩阵运算获得
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
}

cpp 🤖

class NumMatrix {
private:
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    vector<vector<int>> preSum;
    
public:
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = vector<vector<int>>(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个矩阵 [0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // 计算子矩阵 [x1, y1, x2, y2] 的元素和
    int sumRegion(int x1, int y1, int x2, int y2) {
        // 目标矩阵之和由四个相邻矩阵运算获得
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
};

python 🤖

class NumMatrix:
    # 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        if m == 0 or n == 0: return
        # 构造前缀和矩阵
        self.preSum = [[0 for _ in range(n+1)] for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                # 计算每个矩阵 [0, 0, i, j] 的元素和
                self.preSum[i][j] = self.preSum[i-1][j] + self.preSum[i][j-1] + matrix[i-1][j-1] - self.preSum[i-1][j-1]

    # 计算子矩阵 [x1, y1, x2, y2] 的元素和
    def sumRegion(self, x1: int, y1: int, x2: int, y2: int) -> int:
        # 目标矩阵之和由四个相邻矩阵运算获得
        return self.preSum[x2+1][y2+1] - self.preSum[x1][y2+1] - self.preSum[x2+1][y1] + self.preSum[x1][y1]

go 🤖

type NumMatrix struct {
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    preSum [][]int
}

func Constructor(matrix [][]int) NumMatrix {
    m, n := len(matrix), len(matrix[0])
    if m == 0 || n == 0 {
        return NumMatrix{}
    }
    // 构造前缀和矩阵
    preSum := make([][]int, m+1)
    for i := 0; i <= m; i++ {
        preSum[i] = make([]int, n+1)
    }
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            // 计算每个矩阵 [0, 0, i, j] 的元素和
            preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i-1][j-1] - preSum[i-1][j-1]
        }
    }
    return NumMatrix{preSum: preSum}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
func (this *NumMatrix) SumRegion(x1 int, y1 int, x2 int, y2 int) int {
    // 目标矩阵之和由四个相邻矩阵运算获得
    return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1]
}

javascript 🤖

var NumMatrix = function(matrix) {
    var m = matrix.length, n = matrix[0].length;
    if (m === 0 || n === 0) return;
    // 构造前缀和矩阵
    this.preSum = new Array(m + 1).fill(null).map(() => new Array(n + 1).fill(0));
    for (var i = 1; i <= m; i++) {
        for (var j = 1; j <= n; j++) {
            // 计算每个矩阵 [0, 0, i, j] 的元素和
            this.preSum[i][j] = this.preSum[i-1][j] + this.preSum[i][j-1] + matrix[i - 1][j - 1] - this.preSum[i-1][j-1];
        }
    }
};

// 计算子矩阵 [x1, y1, x2, y2] 的元素和
NumMatrix.prototype.sumRegion = function(x1, y1, x2, y2) {
    // 目标矩阵之和由四个相邻矩阵运算获得
    return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1];
};

这样，sumRegion 函数的时间复杂度也用前缀和技巧优化到了 O(1)，这是典型的「空间换时间」思路。

前缀和技巧就讲到这里，应该说这个算法技巧是会者不难难者不会，实际运用中还是要多培养自己的思维灵活性，做到一眼看出题目是一个前缀和问题。

除了本文举例的基本用法，前缀和数组经常和其他数据结构或算法技巧相结合，我会在前缀和技巧高频习题中举例讲解。

引用本文的题目

安装我的 Chrome 刷题插件点开下列题目可直接查看解题思路：

LeetCode	力扣	难度
1314. Matrix Block Sum	1314. 矩阵区域和	🟠
1352. Product of the Last K Numbers	1352. 最后 K 个数的乘积	🟠
238. Product of Array Except Self	238. 除自身以外数组的乘积	🟠
325. Maximum Size Subarray Sum Equals k🔒	325. 和等于 k 的最长子数组长度🔒	🟠
327. Count of Range Sum	327. 区间和的个数	🔴
437. Path Sum III	437. 路径总和 III	🟠
523. Continuous Subarray Sum	523. 连续的子数组和	🟠
525. Contiguous Array	525. 连续数组	🟠
560. Subarray Sum Equals K	560. 和为 K 的子数组	🟠
724. Find Pivot Index	724. 寻找数组的中心下标	🟢
862. Shortest Subarray with Sum at Least K	862. 和至少为 K 的最短子数组	🔴
918. Maximum Sum Circular Subarray	918. 环形子数组的最大和	🟠
974. Subarray Sums Divisible by K	974. 和可被 K 整除的子数组	🟠
-	剑指 Offer 57 - II. 和为s的连续正数序列	🟢
-	剑指 Offer II 010. 和为 k 的子数组	🟠
-	剑指 Offer II 011. 0 和 1 个数相同的子数组	🟠
-	剑指 Offer II 012. 左右两边子数组的和相等	🟢
-	剑指 Offer II 013. 二维子矩阵的和	🟠
-	剑指 Offer II 050. 向下的路径节点之和	🟠

小而美的算法技巧：前缀和数组

303. 区域和检索 - 数组不可变 https://leetcode.cn/problems/range-sum-query-immutable

303. Range Sum Query - Immutable https://leetcode.com/problems/range-sum-query-immutable

304. 二维区域和检索 - 矩阵不可变 https://leetcode.cn/problems/range-sum-query-2d-immutable

304. Range Sum Query 2D - Immutable https://leetcode.com/problems/range-sum-query-2d-immutable

一维数组中的前缀和

二维矩阵中的前缀和