拓展:如何实现一个计算器
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 224. Basic Calculator | 224. 基本计算器 | 🔴 |
| 227. Basic Calculator II | 227. 基本计算器 II | 🟠 |
| 772. Basic Calculator III🔒 | 772. 基本计算器 III🔒 | 🔴 |
我们最终要实现的计算器功能如下:
1、输入一个字符串,可以包含 + - * /、数字、括号以及空格,你的算法返回运算结果。
2、要符合运算法则,括号的优先级最高,先乘除后加减。
3、除号是整数除法,无论正负都向 0 取整(5/2=2,-5/2=-2)。
4、可以假定输入的算式一定合法,且计算过程不会出现整型溢出,不会出现除数为 0 的意外情况。
比如输入如下字符串,算法会返回 9:
3 * (2 - 6 / (3 - 7))
= 3 * (2 - 6 / (-4))
= 3 * (2 - (-1))
= 9可以看到,这就已经非常接近我们实际生活中使用的计算器了,虽然我们以前肯定都用过计算器,但是如果简单思考一下其算法实现,就会大惊失色:
1、按照常理处理括号,要先计算最内层的括号,然后向外慢慢化简。这个过程我们手算都容易出错,何况写成算法呢!
2、要做到先乘除,后加减,这一点教会小朋友还不算难,但教给计算机恐怕有点困难。
3、要处理空格。我们为了美观,习惯性在数字和运算符之间打个空格,但是计算之中得想办法忽略这些空格。
我记得很多大学数据结构的教材上,在讲栈这种数据结构的时候,应该都会用计算器举例,但是有一说一,讲的真的垃圾,不知道多少未来的计算机科学家就被这种简单的数据结构劝退了。
那么本文就来聊聊怎么实现上述一个功能完备的计算器功能,关键在于层层拆解问题,化整为零,逐个击破,几条简单的算法规则就可以处理极其复杂的运算,相信这种思维方式能帮大家解决各种复杂问题。
下面就来拆解,从最简单的一个问题开始。
一、字符串转整数
是的,就是这么一个简单的问题,首先告诉我,怎么把一个字符串形式的正整数,转化成 int 型?
String s = "458";
int n = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
n = 10 * n + (c - '0');
}
// n 现在就等于 458std::string s = "458";
int n = 0;
for (int i = 0; i < s.length(); i++) {
char c = s[i];
n = 10 * n + (c - '0');
}
// n 现在就等于 458s = "458"
n = 0
for i in range(len(s)):
c = s[i]
n = 10 * n + (ord(c) - ord('0'))
# n 现在就等于 458s := "458"
n := 0
for i := 0; i < len(s); i++ {
c := int(s[i] - '0')
n = 10*n + c
}
// n 现在就等于 458var s = "458";
var n = 0;
for (var i = 0; i < s.length; i++) {
var c = s.charAt(i);
n = 10 * n + (c.charCodeAt(0) - '0'.charCodeAt(0));
}
// n 现在就等于 458这个还是很简单的吧,老套路了。但是即便这么简单,依然有坑:(c - '0') 的这个括号不能省略,否则可能造成整型溢出。
因为变量 c 是一个 ASCII 码,如果不加括号就会先加后减,想象一下 s 如果接近 INT_MAX,就会溢出。所以用括号保证先减后加才行。
二、处理加减法
现在进一步,如果输入的这个算式只包含加减法,而且不存在空格,你怎么计算结果?我们拿字符串算式 1-12+3 为例,来说一个很简单的思路:
1、先给第一个数字加一个默认符号 +,变成 +1-12+3。
2、把一个运算符和数字组合成一对儿,也就是三对儿 +1,-12,+3,把它们转化成数字,然后放到一个栈中。
3、将栈中所有的数字求和,就是原算式的结果。
我们直接看代码,结合一张图就看明白了:
int calculate(String s) {
Stack<Integer> stk = new Stack<>();
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
// 如果是数字,连续读取到 num
if (Character.isDigit(c)) {
num = 10 * num + (c - '0');
}
// 如果不是数字,就是遇到了下一个符号,或者是算式的末尾
// 那么之前的数字和符号就要存进栈中
if (c == '+' || c == '-' || i == s.length() - 1) {
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.isEmpty()) {
res += stk.pop();
}
return res;
}int calculate(string s) {
stack<int> stk;
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s[i];
// 如果是数字,连续读取到 num
if (isdigit(c)) {
num = 10 * num + (c - '0');
}
// 如果不是数字,就是遇到了下一个符号,或者是算式的末尾
// 那么之前的数字和符号就要存进栈中
if (c == '+' || c == '-' || i == s.length() - 1) {
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.empty()) {
res += stk.top();
stk.pop();
}
return res;
}def calculate(s):
stk = []
# 记录算式中的数字
num = 0
# 记录 num 前的符号,初始化为 +
sign = '+'
for i in range(len(s)):
c = s[i]
# 如果是数字,连续读取到 num
if c.isdigit():
num = 10 * num + int(c)
# 如果不是数字,就是遇到了下一个符号,或者是算式的末尾
# 那么之前的数字和符号就要存进栈中
if c == '+' or c == '-' or i == len(s) - 1:
if sign == '+':
stk.append(num)
elif sign == '-':
stk.append(-num)
# 更新符号为当前符号,数字清零
sign = c
num = 0
# 将栈中所有结果求和就是答案
res = 0
while stk:
res += stk.pop()
return resfunc calculate(s string) int {
// 记录算式中的数字
var num int
// 最后的结果
var res int
// 记录 num 前的符号,初始化为 +
var sign int = 1
// 栈初始化
stk := stack.New()
// 开始按顺序遍历 s
for i := 0; i < len(s); i++ {
// 如果是数字,连续读取到 num
if isDigit(s[i]) {
num = 10*num + int(s[i]-'0')
}
// 如果不是数字,就是遇到了下一个符号,或者是算式的末尾
// 那么之前的数字和符号就要存进栈中
if s[i] == '+' || s[i] == '-' || i == len(s)-1 {
// 将数字和符号存入栈中
if sign == 1 {
stk.Push(num)
} else if sign == -1 {
stk.Push(-num)
}
// 更新符号为当前符号,数字清零
num = 0
if s[i] == '+' {
sign = 1
} else if s[i] == '-' {
sign = -1
}
}
}
// 将栈中所有结果求和就是答案
for stk.Len() != 0 {
res += stk.Pop().(int)
}
// 返回结果
return res
}
// 辅助函数,判断字符是否为数字
func isDigit(n byte) bool {
if '0' <= n && n <= '9' {
return true
}
return false
}var calculate = function(s) {
// 声明一个数组代替原来的Java栈
var stk = [];
// 记录算式中的数字
var num = 0;
// 记录 num 前的符号,初始化为 +
var sign = '+';
for (var i = 0; i < s.length; i++) {
var c = s.charAt(i);
// 如果是数字,连续读取到 num
if (!isNaN(c)) {
num = 10 * num + (c - '0');
}
// 如果不是数字,就是遇到了下一个符号,或者是算式的末尾
// 那么之前的数字和符号就要存进栈中
if (c === '+' || c === '-' || i === s.length - 1) {
switch(sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
var res = 0;
while (stk.length !== 0) {
res += stk.pop();
}
return res;
}我估计就是中间带 switch 语句的部分有点不好理解吧,i 就是从左到右扫描,sign 和 num 跟在它身后。当 s[i] 遇到一个运算符时,情况是这样的:
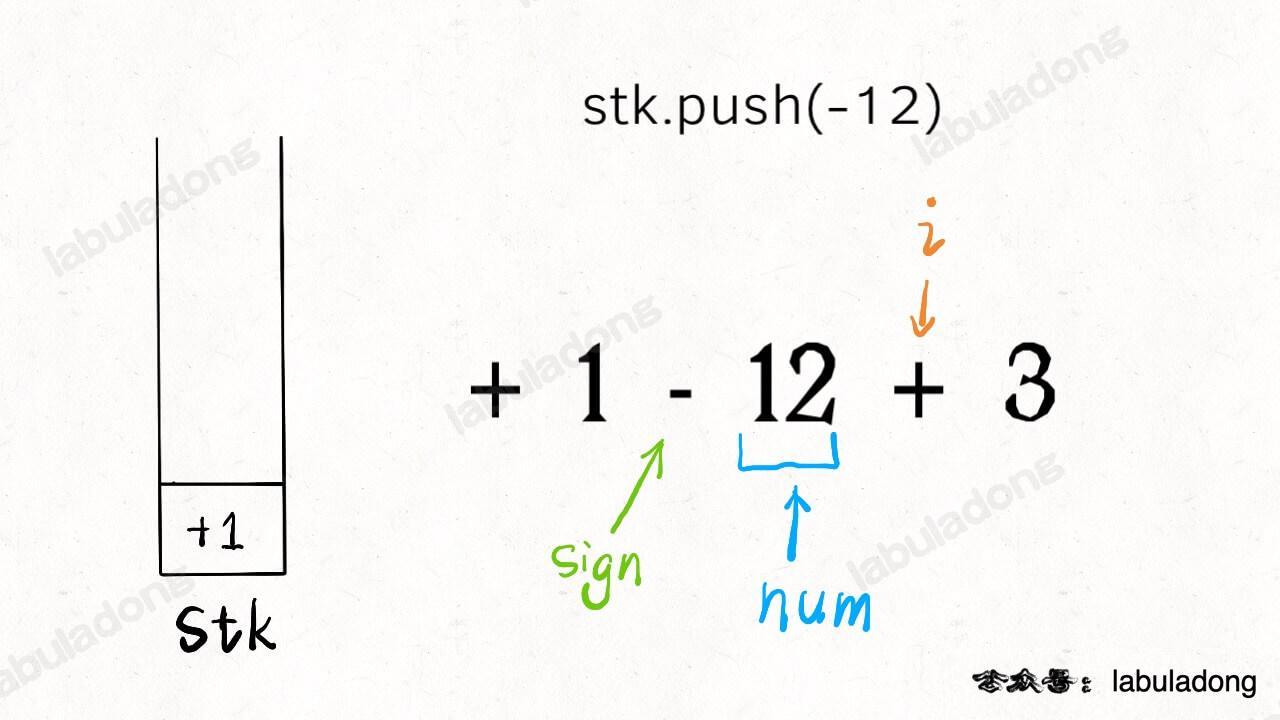
所以说,此时要根据 sign 的 case 不同选择 nums 的正负号,存入栈中,然后更新 sign 并清零 nums 记录下一对儿符合和数字的组合。
另外注意,不只是遇到新的符号会触发入栈,当 i 走到了算式的尽头(i == s.size() - 1 ),也应该将前面的数字入栈,方便后续计算最终结果。
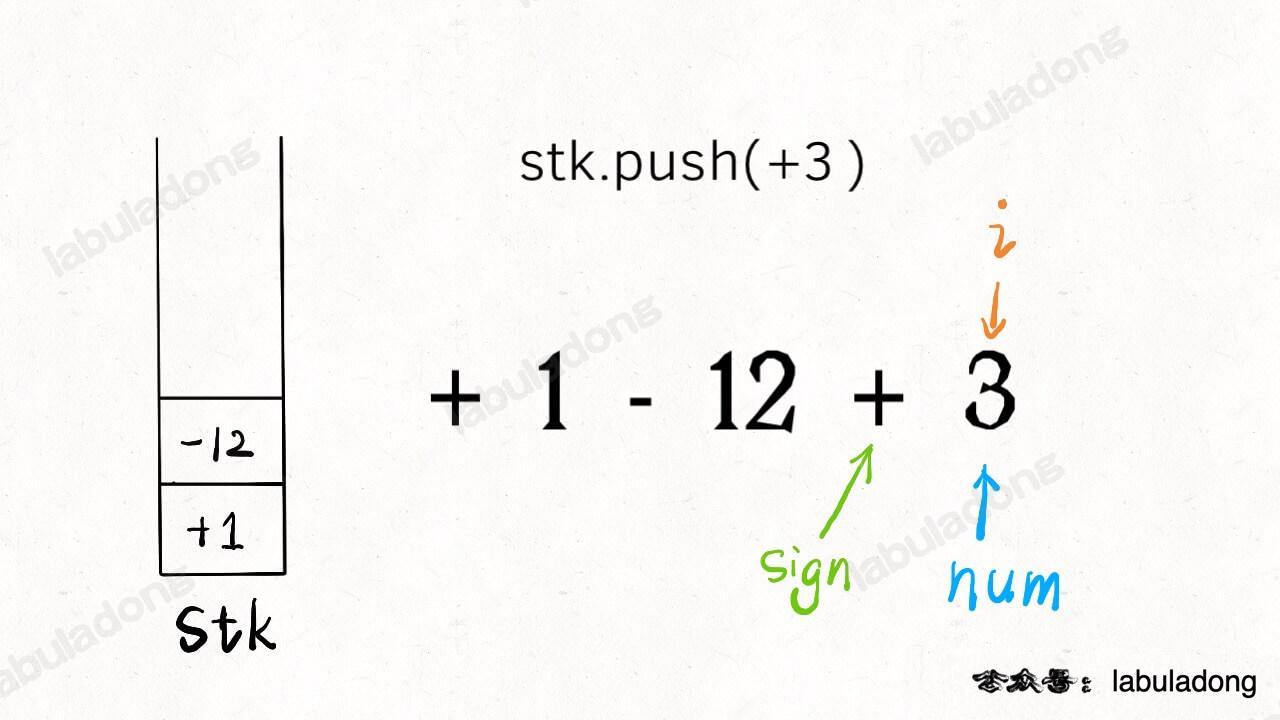
至此,仅处理紧凑加减法字符串的算法就完成了,请确保理解以上内容,后续的内容就基于这个框架修修改改就完事儿了。
三、处理乘除法
其实思路跟仅处理加减法没啥区别,拿字符串 2-3*4+5 举例,核心思路依然是把字符串分解成符号和数字的组合。
比如上述例子就可以分解为 +2,-3,*4,+5 几对儿,我们刚才不是没有处理乘除号吗,很简单,其他部分都不用变,在 switch 部分加上对应的 case 就行了:
int calculate(String s) {
Stack<Integer> stk = new Stack<>();
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '+' || c == '-' || c == '/' || c == '*' || i == s.length() - 1) {
int pre;
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.pop();
stk.push(pre / num);
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.isEmpty()) {
res += stk.pop();
}
return res;
}int calculate(string s) {
stack<int> stk;
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = 0; i < s.length(); i++) {
char c = s[i];
if (isdigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '+' || c == '-' || c == '/' || c == '*' || i == s.length() - 1) {
int pre;
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk.top(); stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.top(); stk.pop();
stk.push(pre / num);
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.empty()) {
res += stk.top(); stk.pop();
}
return res;
}def calculate(s: str) -> int:
stk = []
# 记录算式中的数字
num = 0
# 记录 num 前的符号,初始化为 +
sign = "+"
for i in range(len(s)):
if s[i].isdigit():
num = 10 * num + int(s[i])
# 遇到 +,-,*,/ 或者到了最末尾
if s[i] in "+-*/" or i == len(s) - 1:
if sign == "+":
stk.append(num)
elif sign == "-":
stk.append(-num)
# 只要拿出前一个数字做对应运算即可
elif sign == "*":
stk[-1] *= num
else:
# 遇到除号,需要拿出前一个数字做除法
stk[-1] = int(stk[-1] / num)
# 更新符号为当前符号,数字清零
sign = s[i]
num = 0
# 将栈中所有结果求和就是答案
return sum(stk)func calculate(s string) int {
// 初始化栈stk
stk := make([]int, 0)
// 记录算式中的数字
num := 0
// 记录 num 前的符号,初始化为 +
sign := '+'
for i, c := range s {
if unicode.IsDigit(c) {
num = 10*num + int(c-'0')
}
if c=='+' || c=='-' || c=='/' || c=='*' || i==len(s)-1 {
var pre int
switch sign {
case '+':
// 若符号为+,则数字入栈
stk = append(stk, num)
case '-':
// 若符号为-,则数字取反入栈
stk = append(stk, -num)
case '*':
// 若符号为*,则将栈顶元素出栈,与当前数字相乘,结果再入栈
pre = stk[len(stk)-1]
stk = stk[:len(stk)-1]
stk = append(stk, pre*num)
case '/':
// 若符号为/,则将栈顶元素出栈,除以当前数字,结果再入栈
pre = stk[len(stk)-1]
stk = stk[:len(stk)-1]
stk = append(stk, pre/num)
}
// 更新符号为当前符号,数字清零
sign = rune(c)
num = 0
}
}
// 将栈中所有结果求和就是答案
res := 0
for _, v := range stk {
res += v
}
return res
}var calculate = function(s) {
var stack = [];
// 记录算式中的数字
var num = 0;
// 记录 num 前的符号,初始化为 +
var sign = '+';
for (var i = 0; i < s.length; i++) {
var c = s[i];
if (!isNaN(c)) {
num = 10 * num + (c - '0');
}
if (c === '+' || c === '-' || c === '/' || c === '*' || i === s.length - 1) {
var pre;
switch (sign) {
// 只要拿出前一个数字做对应运算即可
case '+':
stack.push(num); break;
case '-':
stack.push(-num); break;
case '*':
pre = stack.pop();
stack.push(pre * num);
break;
case '/':
pre = stack.pop();
stack.push(Math.trunc(pre / num));
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
var res = 0;
while (stack.length !== 0) {
res += stack.pop();
}
return res;
};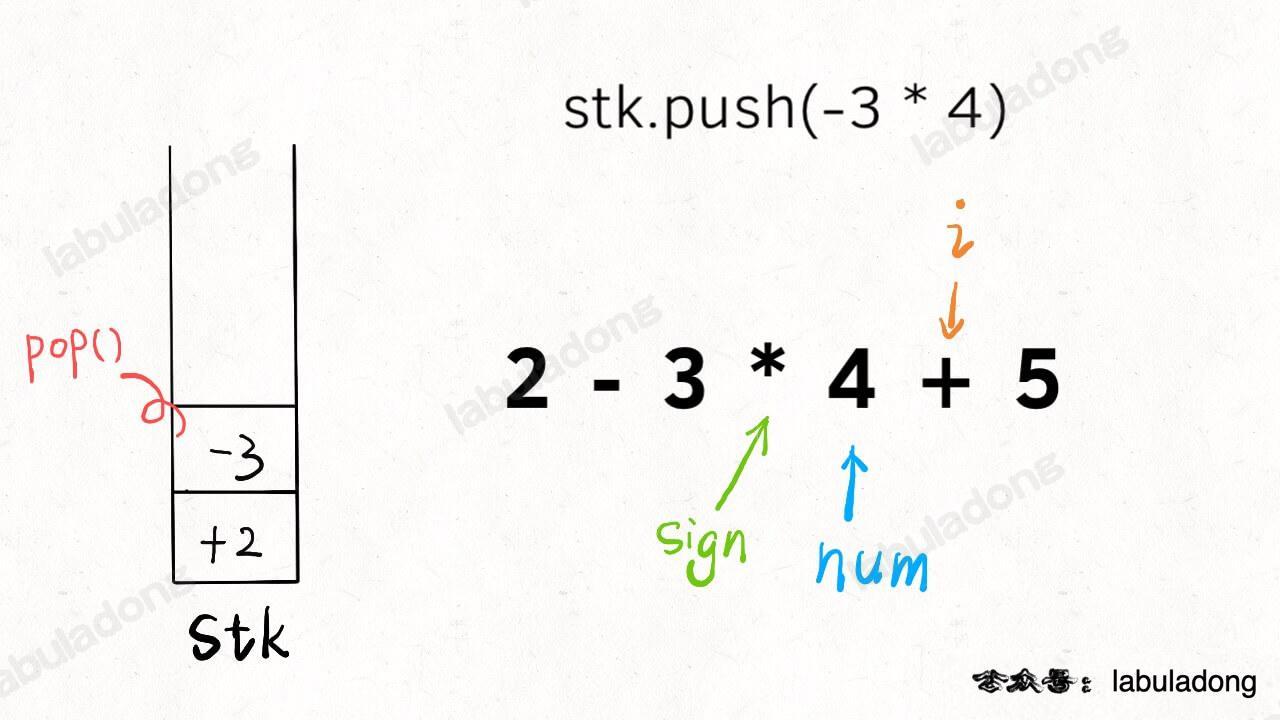
乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈。
现在我们思考一下如何处理字符串中可能出现的空格字符。其实按照目前的代码,我们根本不用特殊处理空格字符,你注意 if 条件,当字符 c 是空格时,不会对它做任何处理,直接跳过了。
好了,我们现在的算法已经可以按照正确的法则计算加减乘除,并且自动忽略空格符,剩下的就是如何让算法正确识别括号了。