二叉搜索树心法(构造篇)
原创
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 95. Unique Binary Search Trees II | 95. 不同的二叉搜索树 II | 🟠 |
| 96. Unique Binary Search Trees | 96. 不同的二叉搜索树 | 🟠 |
之前写了两篇手把手刷 BST 算法题的文章,第一篇 讲了中序遍历对 BST 的重要意义,第二篇 写了 BST 的基本操作。
本文就来写手把手刷 BST 系列的第三篇,循序渐进地讲两道题,如何计算所有有效 BST。
第一道题是力扣第 96 题「不同的二叉搜索树」:
96. 不同的二叉搜索树 | 力扣 | LeetCode | 🟠
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
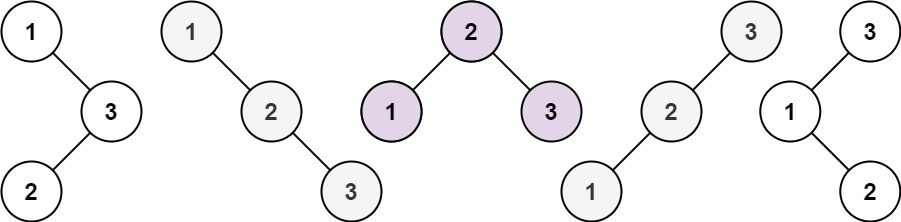
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
函数签名如下:
java
int numTrees(int n);cpp
int numTrees(int n);python
def numTrees(n: int) -> int:go
func numTrees(n int) int {}javascript
var numTrees = function(n) {
};这就是一个正宗的穷举问题,那么什么方式能够正确地穷举有效 BST 的数量呢?
我们前文说过,不要小看「穷举」,这是一件看起来简单但是比较有技术含量的事情,问题的关键就是不能数漏,也不能数多,你咋整?
之前 手把手刷二叉树第一期 说过,二叉树算法的关键就在于明确根节点需要做什么,其实 BST 作为一种特殊的二叉树,核心思路也是一样的。