跳至主要內容

二叉搜索树心法（基操篇）

labuladong原创约 3066 字

450. 删除二叉搜索树中的节点 https://leetcode.cn/problems/delete-node-in-a-bst

450. Delete Node in a BST https://leetcode.com/problems/delete-node-in-a-bst

700. 二叉搜索树中的搜索 https://leetcode.cn/problems/search-in-a-binary-search-tree

700. Search in a Binary Search Tree https://leetcode.com/problems/search-in-a-binary-search-tree

701. 二叉搜索树中的插入操作 https://leetcode.cn/problems/insert-into-a-binary-search-tree

701. Insert into a Binary Search Tree https://leetcode.com/problems/insert-into-a-binary-search-tree

98. 验证二叉搜索树 https://leetcode.cn/problems/validate-binary-search-tree

98. Validate Binary Search Tree https://leetcode.com/problems/validate-binary-search-tree

本文讲解的例题

LeetCode力扣难度
700. Search in a Binary Search Tree700. 二叉搜索树中的搜索🟢
701. Insert into a Binary Search Tree701. 二叉搜索树中的插入操作🟠
450. Delete Node in a BST450. 删除二叉搜索树中的节点🟠
98. Validate Binary Search Tree98. 验证二叉搜索树🟠

前置知识

阅读本文前，你需要先学习：

我们前文 二叉搜索树心法（特性篇） 介绍了 BST 的基本特性，还利用二叉搜索树「中序遍历有序」的特性来解决了几道题目，本文来实现 BST 的基础操作：判断 BST 的合法性、增、删、查。其中「删」和「判断合法性」略微复杂。

BST 的基础操作主要依赖「左小右大」的特性，可以在二叉树中做类似二分搜索的操作，寻找一个元素的效率很高。比如下面这就是一棵合法的二叉树：

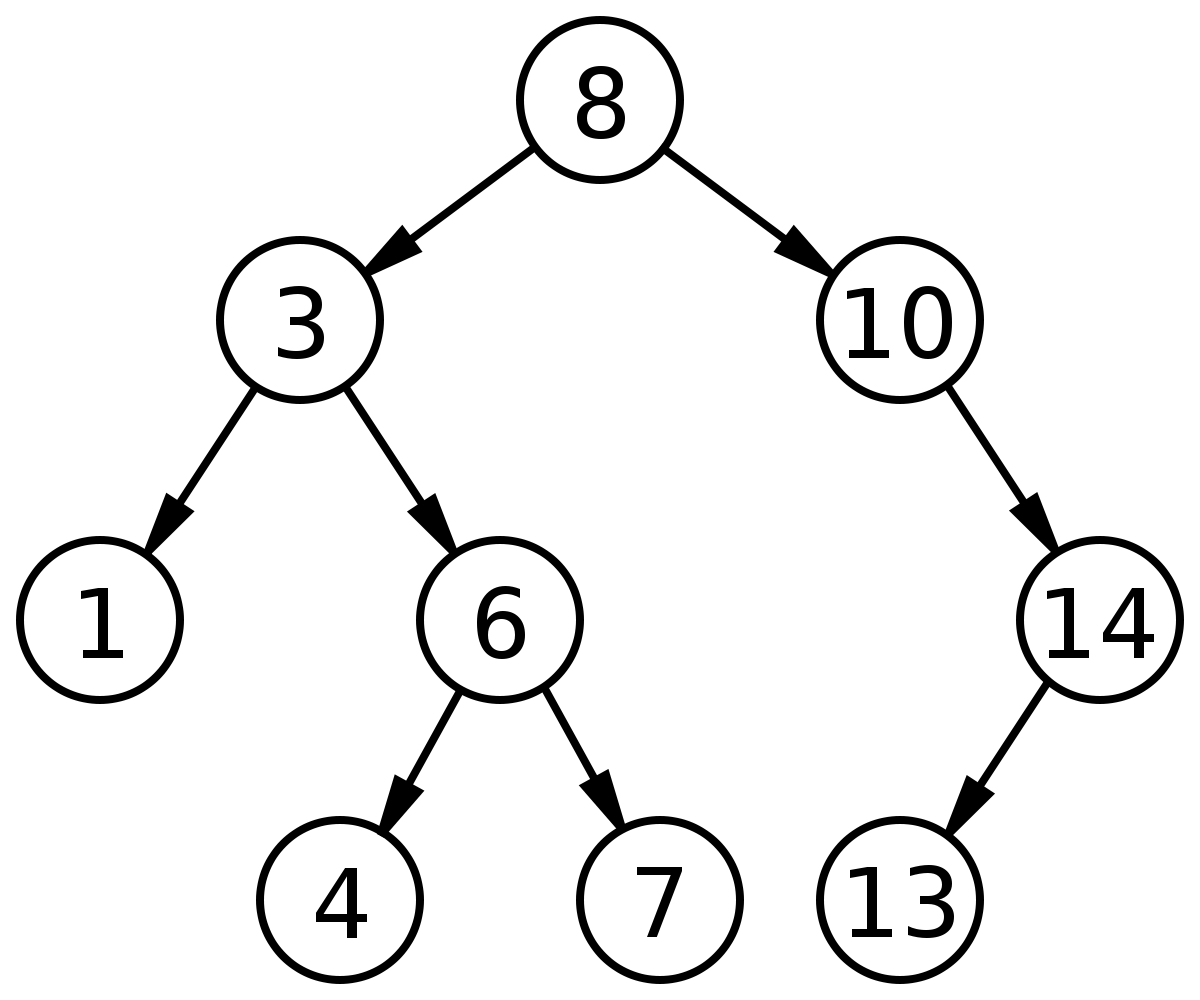
对于 BST 相关的问题，你可能会经常看到类似下面这样的代码逻辑：

java 🟢
void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target) 
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

这个代码框架其实和二叉树的遍历框架差不多，无非就是利用了 BST 左小右大的特性而已。接下来看下 BST 这种结构的基础操作是如何实现的。

一、判断 BST 的合法性

力扣第 98 题「验证二叉搜索树」就是让你判断输入的 BST 是否合法：

98. 验证二叉搜索树 | 力扣 | LeetCode |

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

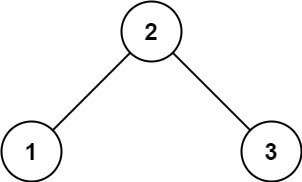
输入：root = [2,1,3]
输出：true

示例 2：

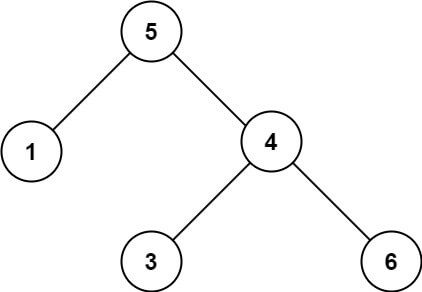
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

  • 树中节点数目范围在[1, 104] 内
  • -231 <= Node.val <= 231 - 1

注意，这里是有坑的哦。按照 BST 左小右大的特性，每个节点想要判断自己是否是合法的 BST 节点，要做的事不就是比较自己和左右孩子吗？感觉应该这样写代码：

java 🟢
boolean isValidBST(TreeNode root) {
    if (root == null) return true;
    // root 的左边应该更小
    if (root.left != null && root.left.val >= root.val)
        return false;
    // root 的右边应该更大
    if (root.right != null && root.right.val <= root.val)
        return false;

    return isValidBST(root.left)
        && isValidBST(root.right);
}

但是这个算法出现了错误，BST 的每个节点应该要小于右边子树的所有节点，下面这个二叉树显然不是 BST，因为节点 10 的右子树中有一个节点 6，但是我们的算法会把它判定为合法 BST：

错误的原因在于，对于每一个节点 root，代码值检查了它的左右孩子节点是否符合左小右大的原则；但是根据 BST 的定义，root 的整个左子树都要小于 root.val，整个右子树都要大于 root.val。

问题是，对于某一个节点 root，他只能管得了自己的左右子节点，怎么把 root 的约束传递给左右子树呢？请看正确的代码：

java 🟢
class Solution {
    public boolean isValidBST(TreeNode root) {
        return _isValidBST(root, null, null);
    }

    // 定义：该函数返回 root 为根的子树的所有节点是否满足 max.val > root.val > min.val
    public boolean _isValidBST(TreeNode root, TreeNode min, TreeNode max) {
        // base case
        if (root == null) return true;
        // 若 root.val 不符合 max 和 min 的限制，说明不是合法 BST
        if (min != null && root.val <= min.val) return false;
        if (max != null && root.val >= max.val) return false;
        // 根据定义，限定左子树的最大值是 root.val，右子树的最小值是 root.val
        return _isValidBST(root.left, min, root) 
            && _isValidBST(root.right, root, max);
    }
}

我们通过使用辅助函数，增加函数参数列表，在参数中携带额外信息，将这种约束传递给子树的所有节点，这也是二叉树算法的一个小技巧吧。

在 BST 中搜索元素

力扣第 700 题「二叉搜索树中的搜索」就是让你在 BST 中搜索值为 target 的节点，函数签名如下：

java 🟢
TreeNode searchBST(TreeNode root, int target);

如果是在一棵普通的二叉树中寻找，可以这样写代码：

java 🟢
TreeNode searchBST(TreeNode root, int target) {
    if (root == null) return null;
    if (root.val == target) return root;
    // 当前节点没找到就递归地去左右子树寻找
    TreeNode left = searchBST(root.left, target);
    TreeNode right = searchBST(root.right, target);

    return left != null ? left : right;
}

这样写完全正确，但这段代码相当于穷举了所有节点，适用于所有二叉树。那么应该如何充分利用 BST 的特殊性，把「左小右大」的特性用上？

很简单，其实不需要递归地搜索两边，类似二分查找思想，根据 target 和 root.val 的大小比较，就能排除一边。我们把上面的思路稍稍改动：

java 🟢
TreeNode searchBST(TreeNode root, int target) {
    if (root == null) {
        return null;
    }
    // 去左子树搜索
    if (root.val > target) {
        return searchBST(root.left, target);
    }
    // 去右子树搜索
    if (root.val < target) {
        return searchBST(root.right, target);
    }
    // 当前节点就是目标值
    return root;
}

在 BST 中插入一个数

对数据结构的操作无非遍历 + 访问，遍历就是「找」，访问就是「改」。具体到这个问题，插入一个数，就是先找到插入位置，然后进行插入操作。

因为 BST 一般不会存在值重复的节点，所以我们一般不会在 BST 中插入已存在的值。下面的代码都默认不会向 BST 中插入已存在的值。

上一个问题，我们总结了 BST 中的遍历框架，就是「找」的问题。直接套框架，加上「改」的操作即可。

一旦涉及「改」，就类似二叉树的构造问题，函数要返回 TreeNode 类型，并且要对递归调用的返回值进行接收。

力扣第 701 题「二叉搜索树中的插入操作」就是这个问题：

701. 二叉搜索树中的插入操作 | 力扣 | LeetCode |

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

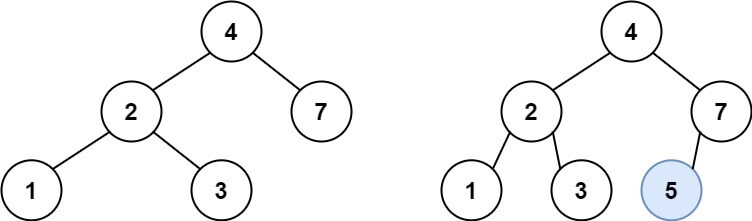
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：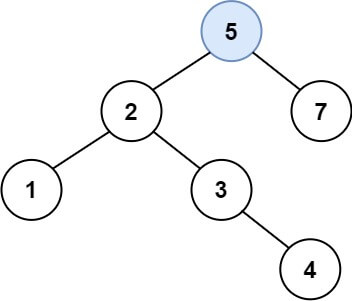

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

  • 树中的节点数将在 [0, 104]的范围内。
  • -108 <= Node.val <= 108
  • 所有值 Node.val 是 独一无二 的。
  • -108 <= val <= 108
  • 保证 val 在原始BST中不存在。

直接看解法代码吧，可以结合注释和可视化面板的来理解：

java 🟢
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            // 找到空位置插入新节点
            return new TreeNode(val);
        }

        // 去右子树找插入位置
        if (root.val < val) {
            root.right = insertIntoBST(root.right, val);
        }
        // 去左子树找插入位置
        if (root.val > val) {
            root.left = insertIntoBST(root.left, val);
        }
        // 返回 root，上层递归会接收返回值作为子节点
        return root;
    }
}

三、在 BST 中删除一个数

力扣第 450 题「删除二叉搜索树中的节点」就是让你在 BST 中删除一个值为 key 的节点：

450. 删除二叉搜索树中的节点 | 力扣 | LeetCode |

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

  1. 首先找到需要删除的节点；
  2. 如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。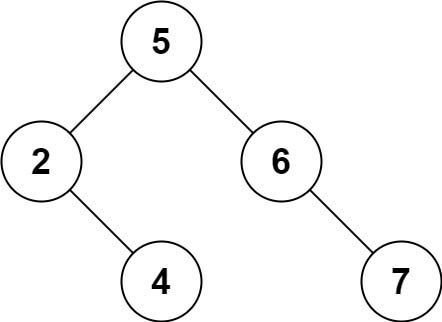

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

  • 节点数的范围 [0, 104].
  • -105 <= Node.val <= 105
  • 节点值唯一
  • root 是合法的二叉搜索树
  • -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

这个问题稍微复杂，跟插入操作类似，先「找」再「改」，先把框架写出来再说：

java 🟢
TreeNode deleteNode(TreeNode root, int key) {
    if (root.val == key) {
        // 找到啦，进行删除
    } else if (root.val > key) {
        // 去左子树找
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        // 去右子树找
        root.right = deleteNode(root.right, key);
    }
    return root;
}

找到目标节点了，比方说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况，用图片来说明。

情况 1：A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了。

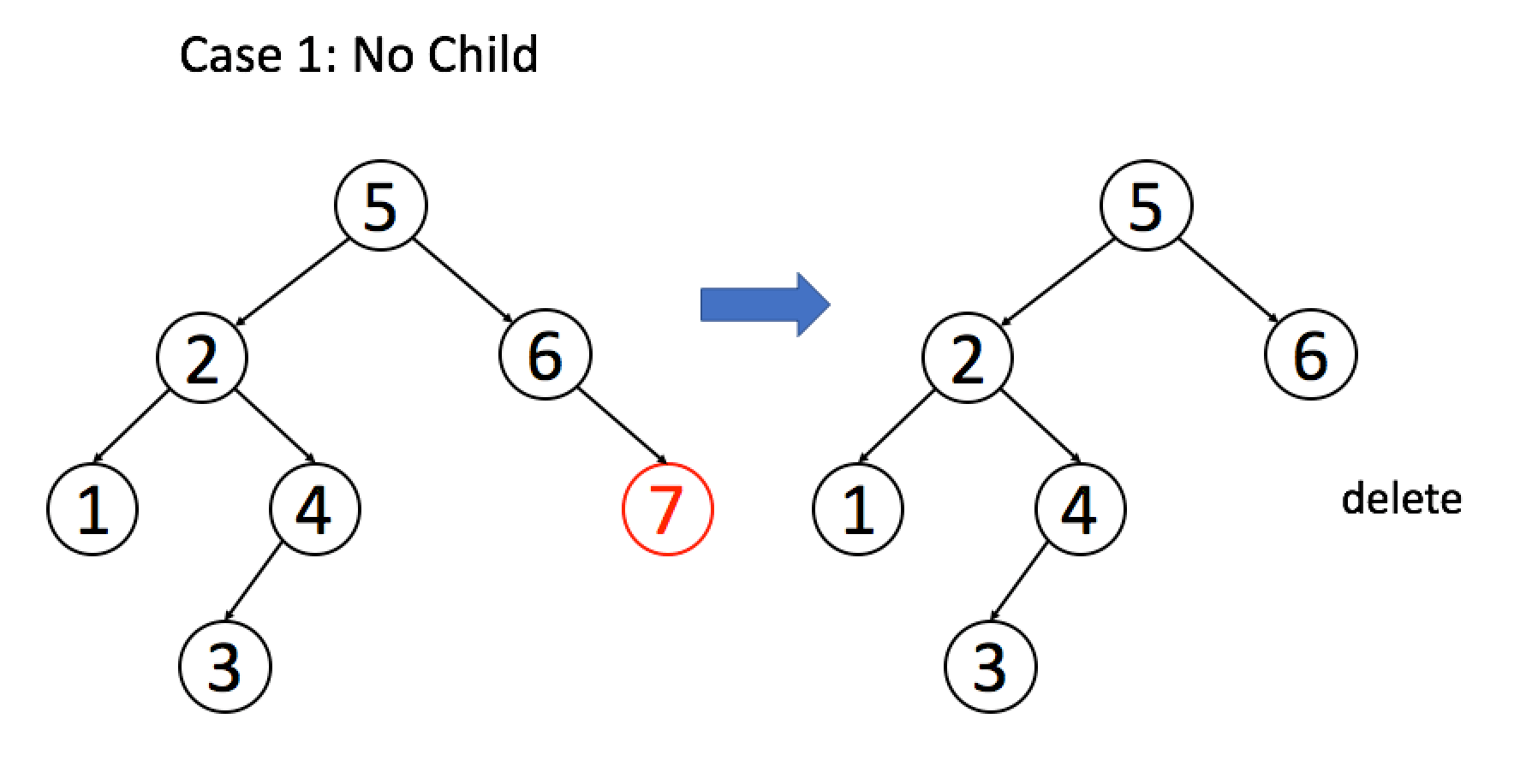
if (root.left == null && root.right == null)
    return null;

情况 2：A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。

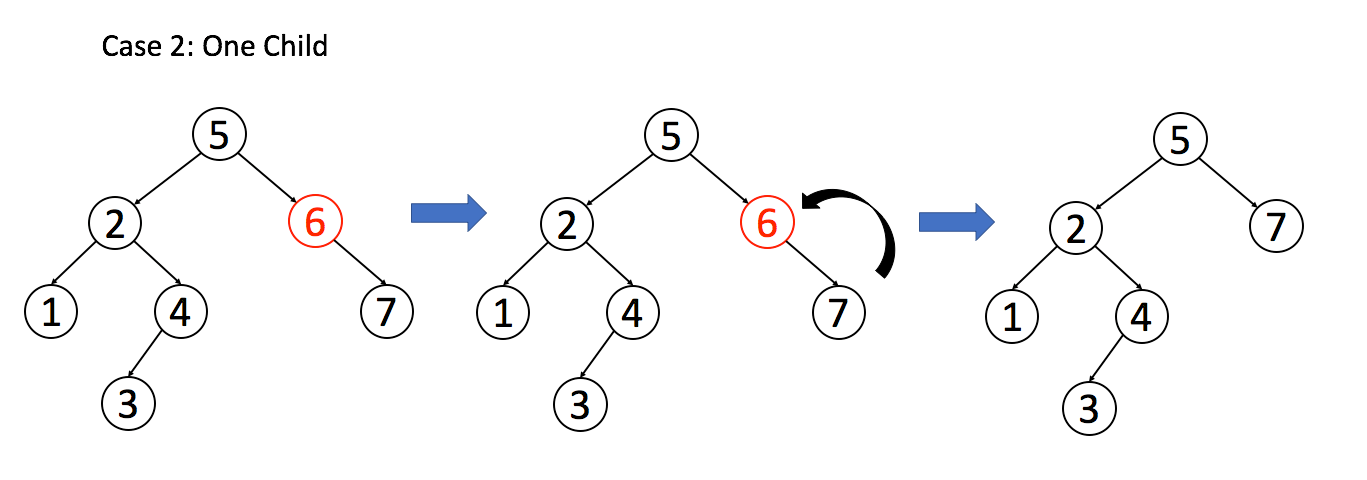
// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;

情况 3：A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。

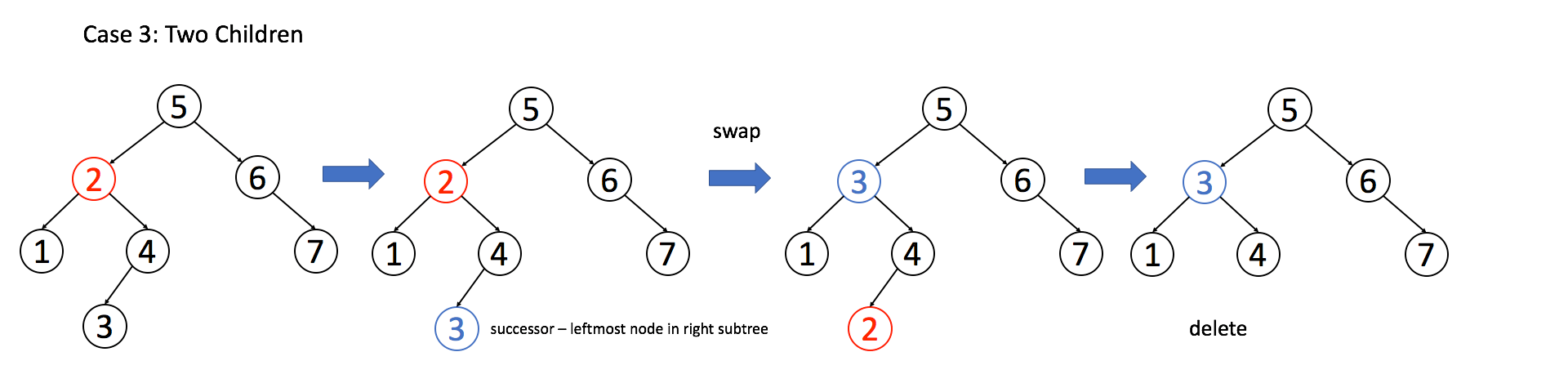
if (root.left != null && root.right != null) {
    // 找到右子树的最小节点
    TreeNode minNode = getMin(root.right);
    // 把 root 改成 minNode
    root.val = minNode.val;
    // 转而去删除 minNode
    root.right = deleteNode(root.right, minNode.val);
}

三种情况分析完毕，填入框架，简化一下代码：

java 🟢
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val == key) {
            // 这两个 if 把情况 1 和 2 都正确处理了
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            // 处理情况 3
            // 获得右子树最小的节点
            TreeNode minNode = getMin(root.right);
            // 删除右子树最小的节点
            root.right = deleteNode(root.right, minNode.val);
            // 用右子树最小的节点替换 root 节点
            minNode.left = root.left;
            minNode.right = root.right;
            root = minNode;
        } else if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        }
        return root;
    }

    TreeNode getMin(TreeNode node) {
        // BST 最左边的就是最小的
        while (node.left != null) node = node.left;
        return node;
    }
}

这样，删除操作就完成了。注意一下，上述代码在处理情况 3 时通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点：

// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;

有的读者可能会疑惑，替换 root 节点为什么这么麻烦，直接改 val 字段不就行了？看起来还更简洁易懂：

// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
root.val = minNode.val;

仅对于这道算法题来说是可以的，但这样操作并不完美，我们一般不会通过修改节点内部的值来交换节点。因为在实际应用中，BST 节点内部的数据域是用户自定义的，可以非常复杂，而 BST 作为数据结构（一个工具人），其操作应该和内部存储的数据域解耦，所以我们更倾向于使用指针操作来交换节点，根本没必要关心内部数据。

最后简单总结一下吧，通过这篇文章，我们总结出了如下几个技巧：

1、如果当前节点会对下面的子节点有整体影响，可以通过辅助函数增长参数列表，借助参数传递信息。

2、掌握 BST 的增删查改方法。

3、递归修改数据结构时，需要对递归调用的返回值进行接收，并返回修改后的节点。

本文就到这里，更多经典的二叉树习题以及递归思维的训练，请参见二叉树章节中的 递归专项练习

引用本文的题目

安装 我的 Chrome 刷题插件 点开下列题目可直接查看解题思路：

LeetCode力扣难度
-剑指 Offer 33. 二叉搜索树的后序遍历序列🟠
上次编辑于: 2024/12/6 11:53:39