二分图判定算法
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 785. Is Graph Bipartite? | 785. 判断二分图 | 🟠 |
| 886. Possible Bipartition | 886. 可能的二分法 | 🟠 |
| - | 剑指 Offer II 106. 二分图 | 🟠 |
今天来讲一个经典图论算法:二分图判定。
二分图简介
先来看二分图的定义:
二分图的顶点集可分割为两个互不相交的子集,图中每条边依附的两个顶点都分属于这两个子集,且两个子集内的顶点不相邻。
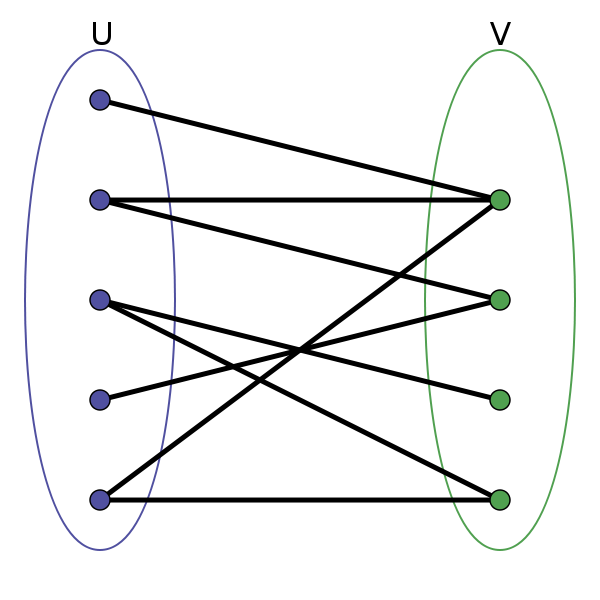
其实图论里面很多术语的定义都比较拗口,不容易理解。我们甭看这个死板的定义了,来玩个游戏吧:
给你一幅「图」,请你用两种颜色将图中的所有顶点着色,且使得任意一条边的两个端点的颜色都不相同,你能做到吗?
这就是图的「双色问题」,其实这个问题就等同于二分图的判定问题,如果你能够成功地将图染色,那么这幅图就是一幅二分图,反之则不是:
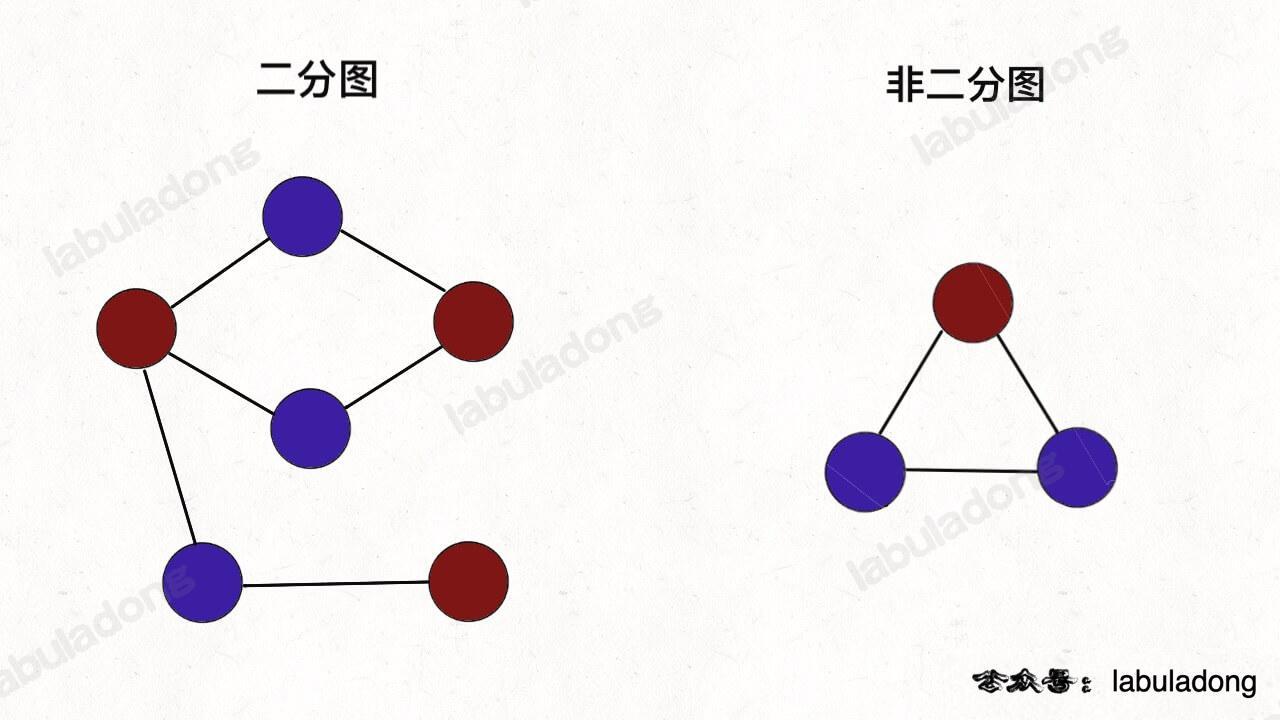
在具体讲解二分图判定算法之前,我们先来说说计算机大佬们闲着无聊解决双色问题的目的是什么。
首先,二分图作为一种特殊的图模型,会被很多高级图算法(比如最大流算法)用到,不过这些高级算法我们不是特别有必要去掌握,有兴趣的读者可以自行搜索。
从简单实用的角度来看,二分图结构在某些场景可以更高效地存储数据。
比如说我们需要一种数据结构来储存电影和演员之间的关系:某一部电影肯定是由多位演员出演的,且某一位演员可能会出演多部电影。你使用什么数据结构来存储这种关系呢?
既然是存储映射关系,最简单的不就是使用 哈希表 嘛,我们可以使用一个 HashMap<String, List<String>> 来存储电影到演员列表的映射,如果给一部电影的名字,就能快速得到出演该电影的演员。
但是如果给出一个演员的名字,我们想快速得到该演员演出的所有电影,怎么办呢?这就需要「反向索引」,对之前的哈希表进行一些操作,新建另一个哈希表,把演员作为键,把电影列表作为值。
显然,如果用哈希表存储,需要两个哈希表分别存储「每个演员到电影列表」的映射和「每部电影到演员列表」的映射。但如果用「图」结构存储,将电影和参演的演员连接,很自然地就成为了一幅二分图:
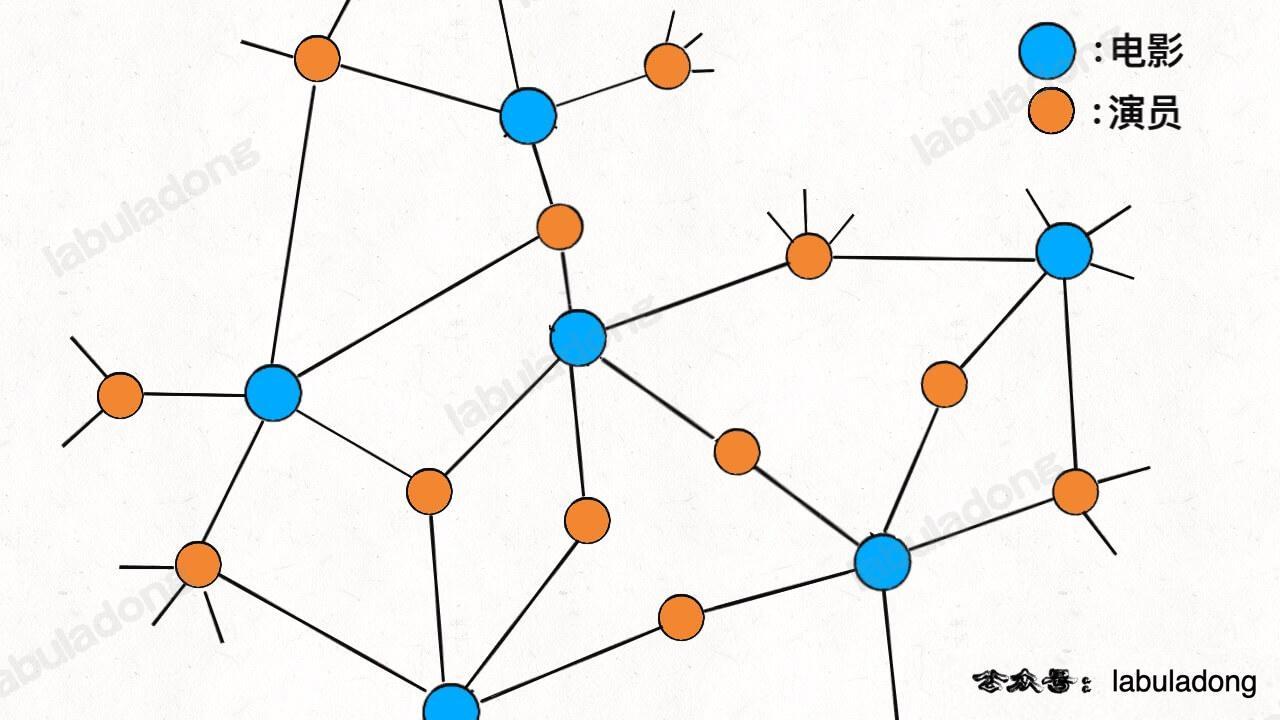
每个电影节点的相邻节点就是参演该电影的所有演员,每个演员的相邻节点就是该演员参演过的所有电影,对比哈希表的存储方式更方便直观,所需的存储空间更小。
其实生活中不少实体的关系都能自然地形成二分图结构,所以在某些场景下图结构也可以作为存储键值对的数据结构(符号表)。
好了,接下来进入正题,说说如何判定一幅图是否是二分图。
二分图判定思路
判定二分图的算法很简单,就是用代码解决「双色问题」。
说白了就是遍历一遍图,一边遍历一边染色,看看能不能用两种颜色给所有节点染色,且相邻节点的颜色都不相同。
既然说到遍历图,也不涉及最短路径之类的,当然是 DFS 算法和 BFS 皆可了,DFS 算法相对更常用些,所以我们先来看看如何用 DFS 算法判定双色图。
首先,基于 图结构的遍历 写出图的 DFS 遍历框架:
// 遍历图的所有节点
void traverse(Graph graph, int s, boolean[] visited) {
// base case
if (s < 0 || s >= graph.size()) {
return;
}
if (visited[s]) {
// 防止死循环
return;
}
// 前序位置
visited[s] = true;
System.out.println("visit " + s);
for (Edge e : graph.neighbors(s)) {
traverse(graph, e.to, visited);
}
// 后序位置
}// 遍历图的所有节点
void traverse(const Graph& graph, int s, std::vector<bool>& visited) {
// base case
if (s < 0 || s >= graph.size()) {
return;
}
if (visited[s]) {
// 防止死循环
return;
}
// 前序位置
visited[s] = true;
std::cout << "visit " << s << std::endl;
for (const Graph::Edge& e : graph.neighbors(s)) {
traverse(graph, e.to, visited);
}
// 后序位置
}# 遍历图的所有节点
def traverse(graph, s, visited):
# base case
if s < 0 or s >= len(graph):
return
if visited[s]:
# 防止死循环
return
# 前序位置
visited[s] = True
print("visit", s)
for e in graph.neighbors(s):
traverse(graph, e.to, visited)
# 后序位置// 遍历图的所有节点
func traverse(graph Graph, s int, visited []bool) {
// base case
if s < 0 || s >= len(graph) {
return
}
if visited[s] {
// 防止死循环
return
}
// 前序位置
visited[s] = true
fmt.Println("visit", s)
for _, e := range graph.neighbors(s) {
traverse(graph, e.to, visited)
}
// 后序位置
}// 遍历图的所有节点
var traverse = function(graph, s, visited) {
// base case
if (s < 0 || s >= graph.size()) {
return;
}
if (visited[s]) {
// 防止死循环
return;
}
// 前序位置
visited[s] = true;
console.log("visit " + s);
for (var e of graph.neighbors(s)) {
traverse(graph, e.to, visited);
}
// 后序位置
};因为图中可能存在环,所以用 visited 数组防止走回头路。
这里可以看到我习惯把 return 语句都放在函数开头,因为一般 return 语句都是 base case,集中放在一起可以让算法结构更清晰。
其实,如果你愿意,也可以把 if 判断放到其它地方,比如图遍历框架可以稍微改改:
// 图遍历框架
boolean[] visited;
void traverse(Graph graph, int v) {
// 前序遍历位置,标记节点 v 已访问
visited[v] = true;
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// 只遍历没标记过的相邻节点
traverse(graph, neighbor);
}
}
}// 图遍历框架
std::vector<bool> visited;
void traverse(Graph &graph, int v) {
// 前序遍历位置,标记节点 v 已访问
visited[v] = true;
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// 只遍历没标记过的相邻节点
traverse(graph, neighbor);
}
}
}# 图遍历框架
visited = []
def traverse(graph: Graph, v: int):
# 前序遍历位置,标记节点 v 已访问
visited[v] = True
for neighbor in graph.neighbors(v):
if not visited[neighbor]:
# 只遍历没标记过的相邻节点
traverse(graph, neighbor)// 定义遍历图的函数
var visited []bool
func traverse(graph *Graph, v int) {
// 前序遍历位置,标记节点 v 已访问
visited[v] = true
for _, neighbor := range graph.neighbors(v) {
if !visited[neighbor] {
// 只遍历没标记过的相邻节点
traverse(graph, neighbor)
}
}
}// 图遍历框架
var visited = [];
var traverse = function(graph, v) {
// 前序遍历位置,标记节点 v 已访问
visited[v] = true;
var neighbors = graph.neighbors(v);
for (var i = 0; i < neighbors.length; i++) {
if (!visited[neighbors[i]]) {
// 只遍历没标记过的相邻节点
traverse(graph, neighbors[i]);
}
}
};这种写法把对 visited 的判断放到递归调用之前,和之前的写法唯一的不同就是,你需要保证调用 traverse(v) 的时候,visited[v] == false。
为什么要特别说这种写法呢?因为我们判断二分图的算法会用到这种写法。
回顾一下二分图怎么判断,其实就是让 traverse 函数一边遍历节点,一边给节点染色,尝试让每对相邻节点的颜色都不一样。
所以,判定二分图的代码逻辑可以这样写:
// 图遍历框架
void traverse(Graph graph, boolean[] visited, int v) {
visited[v] = true;
// 遍历节点 v 的所有相邻节点 neighbor
for (int neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// 相邻节点 neighbor 没有被访问过
// 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
traverse(graph, visited, neighbor);
} else {
// 相邻节点 neighbor 已经被访问过
// 那么应该比较节点 neighbor 和节点 v 的颜色
// 若相同,则此图不是二分图
}
}
}// 图遍历框架
void traverse(Graph &graph, vector<bool> &visited, int v) {
visited[v] = true;
// 遍历节点 v 的所有相邻节点 neighbor
for(auto neighbor : graph.neighbors(v)) {
if (!visited[neighbor]) {
// 相邻节点 neighbor 没有被访问过
// 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
traverse(graph, visited, neighbor);
} else {
// 相邻节点 neighbor 已经被访问过
// 那么应该比较节点 neighbor 和节点 v 的颜色
// 若相同,则此图不是二分图
}
}
}# 图遍历框架
def traverse(graph, visited, v):
visited[v] = True
# 遍历节点 v 的所有相邻节点 neighbor
for neighbor in graph.neighbors(v):
if not visited[neighbor]:
# 相邻节点 neighbor 没有被访问过
# 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
traverse(graph, visited, neighbor)
else:
# 相邻节点 neighbor 已经被访问过
# 那么应该比较节点 neighbor 和节点 v 的颜色
# 若相同,则此图不是二分图
pass// 图遍历框架
func traverse(graph Graph, visited []bool, v int) {
visited[v] = true
// 遍历节点 v 的所有相邻节点 neighbor
for _, neighbor := range graph.neighbors(v) {
if !visited[neighbor] {
// 相邻节点 neighbor 没有被访问过
// 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
traverse(graph, visited, neighbor)
} else {
// 相邻节点 neighbor 已经被访问过
// 那么应该比较节点 neighbor 和节点 v 的颜色
// 若相同,则此图不是二分图
}
}
}// 图遍历框架
var traverse = function(graph, visited, v) {
visited[v] = true;
// 遍历节点 v 的所有相邻节点 neighbor
for (var neighbor of graph.neighbors(v)) {
if (!visited[neighbor]) {
// 相邻节点 neighbor 没有被访问过
// 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
traverse(graph, visited, neighbor);
} else {
// 相邻节点 neighbor 已经被访问过
// 那么应该比较节点 neighbor 和节点 v 的颜色
// 若相同,则此图不是二分图
}
}
}如果你能看懂上面这段代码,就能写出二分图判定的具体代码了,接下来看两道具体的算法题来实操一下。
题目实践
力扣第 785 题「判断二分图」就是原题,题目给你输入一个 邻接表 表示一幅无向图,请你判断这幅图是否是二分图。
函数签名如下:
boolean isBipartite(int[][] graph);bool isBipartite(vector<vector<int>>& graph);def isBipartite(graph: List[List[int]]) -> bool:func isBipartite(graph [][]int) boolvar isBipartite = function(graph) {
};比如题目给的例子,输入的邻接表 graph = [[1,2,3],[0,2],[0,1,3],[0,2]],也就是这样一幅图:
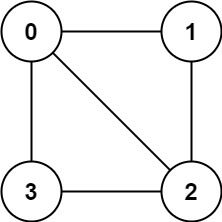
显然无法对节点着色使得每两个相邻节点的颜色都不相同,所以算法返回 false。
但如果输入 graph = [[1,3],[0,2],[1,3],[0,2]],也就是这样一幅图:
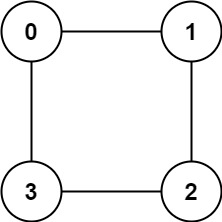
如果把节点 {0, 2} 涂一个颜色,节点 {1, 3} 涂另一个颜色,就可以解决「双色问题」,所以这是一幅二分图,算法返回 true。
结合之前的代码框架,我们可以额外使用一个 color 数组来记录每个节点的颜色,从而写出解法代码:
class Solution {
// 记录图是否符合二分图性质
private boolean ok = true;
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
private boolean[] color;
// 记录图中节点是否被访问过
private boolean[] visited;
// 主函数,输入邻接表,判断是否是二分图
public boolean isBipartite(int[][] graph) {
int n = graph.length;
color = new boolean[n];
visited = new boolean[n];
// 因为图不一定是联通的,可能存在多个子图
// 所以要把每个节点都作为起点进行一次遍历
// 如果发现任何一个子图不是二分图,整幅图都不算二分图
for (int v = 0; v < n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
// DFS 遍历框架
private void traverse(int[][] graph, int v) {
// 如果已经确定不是二分图了,就不用浪费时间再递归遍历了
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v];
// 继续遍历 w
traverse(graph, w);
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if (color[w] == color[v]) {
// 若相同,则此图不是二分图
ok = false;
}
}
}
}
}class Solution {
// 记录图是否符合二分图性质
private:
bool ok = true;
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
vector<bool> color;
// 记录图中节点是否被访问过
vector<bool> visited;
// DFS 遍历框架
void traverse(const vector<vector<int>>& graph, int v) {
// 如果已经确定不是二分图了,就不用浪费时间再递归遍历了
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v];
// 继续遍历 w
traverse(graph, w);
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if (color[w] == color[v]) {
// 若相同,则此图不是二分图
ok = false;
}
}
}
}
public:
// 主函数,输入邻接表,判断是否是二分图
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
color = vector<bool>(n);
visited = vector<bool>(n);
// 因为图不一定是联通的,可能存在多个子图
// 所以要把每个节点都作为起点进行一次遍历
// 如果发现任何一个子图不是二分图,整幅图都不算二分图
for (int v = 0; v < n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
};class Solution:
# 记录图是否符合二分图性质
# 记录图中节点的颜色,false 和 true 代表两种不同颜色
# 记录图中节点是否被访问过
def __init__(self):
self.ok = True
self.color = None
self.visited = None
# 主函数,输入邻接表,判断是否是二分图
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
self.color = [False] * n
self.visited = [False] * n
# 因为图不一定是联通的,可能存在多个子图
# 所以要把每个节点都作为起点进行一次遍历
# 如果发现任何一个子图不是二分图,整幅图都不算二分图
for v in range(n):
if not self.visited[v]:
self.traverse(graph, v)
return self.ok
# DFS 遍历框架
def traverse(self, graph: List[List[int]], v: int) -> None:
# 如果已经确定不是二分图了,就不用浪费时间再递归遍历了
if not self.ok:
return
self.visited[v] = True
for w in graph[v]:
if not self.visited[w]:
# 相邻节点 w 没有被访问过
# 那么应该给节点 w 涂上和节点 v 不同的颜色
self.color[w] = not self.color[v]
# 继续遍历 w
self.traverse(graph, w)
else:
# 相邻节点 w 已经被访问过
# 根据 v 和 w 的颜色判断是否是二分图
if self.color[w] == self.color[v]:
# 若相同,则此图不是二分图
self.ok = False// 主函数,输入邻接表,判断是否是二分图
func isBipartite(graph [][]int) bool {
n := len(graph)
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
color := make([]bool, n)
// 记录图中节点是否被访问过
visited := make([]bool, n)
// 记录图是否符合二分图性质
ok := true
// 因为图不一定是联通的,可能存在多个子图
// 所以要把每个节点都作为起点进行一次遍历
// 如果发现任何一个子图不是二分图,整幅图都不算二分图
for v := 0; v < n; v++ {
if !visited[v] {
traverse(graph, v, color, visited, &ok)
}
}
return ok
}
// DFS 遍历框架
func traverse(graph [][]int, v int, color []bool, visited []bool, ok *bool) {
// 如果已经确定不是二分图了,就不用浪费时间再递归遍历了
if !*ok {
return
}
visited[v] = true
for _, w := range graph[v] {
if !visited[w] {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v]
// 继续遍历 w
traverse(graph, w, color, visited, ok)
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if color[w] == color[v] {
// 若相同,则此图不是二分图
*ok = false
}
}
}
}var isBipartite = function(graph) {
// 记录图是否符合二分图性质
let ok = true;
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
let color = new Array(graph.length).fill(false);
// 记录图中节点是否被访问过
let visited = new Array(graph.length).fill(false);
// DFS 遍历框架
var traverse = function(graph, v) {
// 如果已经确定不是二分图了,就不用浪费时间再递归遍历了
if (!ok) return;
visited[v] = true;
for (let w of graph[v]) {
if (!visited[w]) {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v];
// 继续遍历 w
traverse(graph, w);
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if (color[w] === color[v]) {
// 若相同,则此图不是二分图
ok = false;
}
}
}
};
// 主函数,输入邻接表,判断是否是二分图
let n = graph.length;
// 因为图不一定是联通的,可能存在多个子图
// 所以要把每个节点都作为起点进行一次遍历
// 如果发现任何一个子图不是二分图,整幅图都不算二分图
for (let v = 0; v < n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
};你可以多次点击 visited[v] = true; 这行代码,查看节点的染色过程。
算法可视化面板
接下来看一下 BFS 算法的逻辑:
class Solution {
// 记录图是否符合二分图性质
private boolean ok = true;
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
private boolean[] color;
// 记录图中节点是否被访问过
private boolean[] visited;
public boolean isBipartite(int[][] graph) {
int n = graph.length;
color = new boolean[n];
visited = new boolean[n];
for (int v = 0; v < n; v++) {
if (!visited[v]) {
// 改为使用 BFS 函数
bfs(graph, v);
}
}
return ok;
}
// 从 start 节点开始进行 BFS 遍历
private void bfs(int[][] graph, int start) {
Queue<Integer> q = new LinkedList<>();
visited[start] = true;
q.offer(start);
while (!q.isEmpty() && ok) {
int v = q.poll();
// 从节点 v 向所有相邻节点扩散
for (int w : graph[v]) {
if (!visited[w]) {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v];
// 标记 w 节点,并放入队列
visited[w] = true;
q.offer(w);
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if (color[w] == color[v]) {
// 若相同,则此图不是二分图
ok = false;
return;
}
}
}
}
}
}class Solution {
public:
// 记录图是否符合二分图性质
bool ok = true;
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
vector<bool> color;
// 记录图中节点是否被访问过
vector<bool> visited;
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
color.resize(n);
visited.resize(n);
for (int v = 0; v < n; v++) {
if (!visited[v]) {
// 改为使用 BFS 函数
bfs(graph, v);
}
}
return ok;
}
// 从 start 节点开始进行 BFS 遍历
void bfs(vector<vector<int>>& graph, int start) {
queue<int> q;
visited[start] = true;
q.push(start);
while (!q.empty() && ok) {
int v = q.front();
q.pop();
// 从节点 v 向所有相邻节点扩散
for (int w : graph[v]) {
if (!visited[w]) {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v];
// 标记 w 节点,并放入队列
visited[w] = true;
q.push(w);
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if (color[w] == color[v]) {
// 若相同,则此图不是二分图
ok = false;
return;
}
}
}
}
}
};from collections import deque
class Solution:
def __init__(self):
# 记录图是否符合二分图性质
self.ok = True
# 记录图中节点的颜色,False 和 True 代表两种不同颜色
self.color = []
# 记录图中节点是否被访问过
self.visited = []
def isBipartite(self, graph):
n = len(graph)
self.color = [False]*n
self.visited = [False]*n
for v in range(n):
if not self.visited[v]:
# 改为使用 BFS 函数
self.bfs(graph, v)
return self.ok
# 从 start 节点开始进行 BFS 遍历
def bfs(self, graph, start):
q = deque([start])
self.visited[start] = True
while q and self.ok:
v = q.popleft()
# 从节点 v 向所有相邻节点扩散
for w in graph[v]:
if not self.visited[w]:
# 相邻节点 w 没有被访问过
# 那么应该给节点 w 涂上和节点 v 不同的颜色
self.color[w] = not self.color[v]
# 标记 w 节点,并放入队列
self.visited[w] = True
q.append(w)
else:
# 相邻节点 w 已经被访问过
# 根据 v 和 w 的颜色判断是否是二分图
if self.color[w] == self.color[v]:
# 若相同,则此图不是二分图
self.ok = False
return// 判断是否为二分图
func isBipartite(graph [][]int) bool {
// 记录图是否符合二分图性质
ok := true
n := len(graph)
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
color := make([]bool, n)
// 记录图中节点是否被访问过
visited := make([]bool, n)
// 从 start 节点开始进行 BFS 遍历
var bfs func(start int)
bfs = func(start int) {
q := []int{}
visited[start] = true
q = append(q, start)
for len(q) > 0 && ok {
v := q[0]
q = q[1:]
// 从节点 v 向所有相邻节点扩散
for _, w := range graph[v] {
if !visited[w] {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v]
// 标记 w 节点,并放入队列
visited[w] = true
q = append(q, w)
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if color[w] == color[v] {
// 若相同,则此图不是二分图
ok = false
return
}
}
}
}
}
for v := 0; v < n && ok; v++ {
if !visited[v] {
// 改为使用BFS函数
bfs(v)
}
}
return ok
}var isBipartite = function(graph) {
// 记录图是否符合二分图性质
let ok = true;
// 记录图中节点的颜色,false 和 true 代表两种不同颜色
let color = Array(graph.length);
// 记录图中节点是否被访问过
let visited = Array(graph.length);
// 从 start 节点开始进行 BFS 遍历
var bfs = function(start) {
let q = [];
visited[start] = true;
q.push(start);
while (q.length && ok) {
let v = q.shift();
// 从节点 v 向所有相邻节点扩散
for (let w of graph[v]) {
if (!visited[w]) {
// 相邻节点 w 没有被访问过
// 那么应该给节点 w 涂上和节点 v 不同的颜色
color[w] = !color[v];
// 标记 w 节点,并放入队列
visited[w] = true;
q.push(w);
} else {
// 相邻节点 w 已经被访问过
// 根据 v 和 w 的颜色判断是否是二分图
if (color[w] == color[v]) {
// 若相同,则此图不是二分图
ok = false;
return;
}
}
}
}
};
let n = graph.length;
// 因为图不一定是联通的,可能存在多个子图
// 所以要把每个节点都作为起点进行一次遍历
// 如果发现任何一个子图不是二分图,整幅图都不算二分图
for (let v = 0; v < n; v++) {
if (!visited[v]) {
// 改为使用 BFS 函数
bfs(v);
}
}
return ok;
};核心逻辑和刚才实现的 traverse 函数(DFS 算法)完全一样,也是根据相邻节点 v 和 w 的颜色来进行判断的。关于 BFS 算法框架的探讨,详见前文 BFS 算法框架 和 Dijkstra 算法模板,这里就不展开了。
最后再来看看力扣第 886 题「可能的二分法」:
886. 可能的二分法 | 力扣 | LeetCode | 🟠
给定一组 n 人(编号为 1, 2, ..., n), 我们想把每个人分进任意大小的两组。每个人都可能不喜欢其他人,那么他们不应该属于同一组。
给定整数 n 和数组 dislikes ,其中 dislikes[i] = [ai, bi] ,表示不允许将编号为 ai 和 bi的人归入同一组。当可以用这种方法将所有人分进两组时,返回 true;否则返回 false。
示例 1:
输入:n = 4, dislikes = [[1,2],[1,3],[2,4]] 输出:true 解释:group1 [1,4], group2 [2,3]
示例 2:
输入:n = 3, dislikes = [[1,2],[1,3],[2,3]] 输出:false
示例 3:
输入:n = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]] 输出:false
提示:
1 <= n <= 20000 <= dislikes.length <= 104dislikes[i].length == 21 <= dislikes[i][j] <= nai < bidislikes中每一组都 不同
// 函数签名如下
boolean possibleBipartition(int n, int[][] dislikes);// 函数签名如下
bool possibleBipartition(int n, vector<vector<int>>& dislikes);# 函数签名如下
def possibleBipartition(n: int, dislikes: List[List[int]]):// 函数签名如下
func possibleBipartition(n int, dislikes [][]int) bool// 函数签名如下
var possibleBipartition = function(n, dislikes) {}其实这题考察的就是二分图的判定:
如果你把每个人看做图中的节点,相互讨厌的关系看做图中的边,那么 dislikes 数组就可以构成一幅图;
又因为题目说互相讨厌的人不能放在同一组里,相当于图中的所有相邻节点都要放进两个不同的组;
那就回到了「双色问题」,如果能够用两种颜色着色所有节点,且相邻节点颜色都不同,那么你按照颜色把这些节点分成两组不就行了嘛。
所以解法就出来了,我们把 dislikes 构造成一幅图,然后执行二分图的判定算法即可:
class Solution {
private boolean ok = true;
private boolean[] color;
private boolean[] visited;
public boolean possibleBipartition(int n, int[][] dislikes) {
// 图节点编号从 1 开始
color = new boolean[n + 1];
visited = new boolean[n + 1];
// 转化成邻接表表示图结构
List<Integer>[] graph = buildGraph(n, dislikes);
for (int v = 1; v <= n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
// 建图函数
private List<Integer>[] buildGraph(int n, int[][] dislikes) {
// 图节点编号为 1...n
List<Integer>[] graph = new LinkedList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : dislikes) {
int v = edge[1];
int w = edge[0];
// 「无向图」相当于「双向图」
// v -> w
graph[v].add(w);
// w -> v
graph[w].add(v);
}
return graph;
}
// 和之前判定二分图的 traverse 函数完全相同
private void traverse(List<Integer>[] graph, int v) {
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
color[w] = !color[v];
traverse(graph, w);
} else {
if (color[w] == color[v]) {
ok = false;
}
}
}
}
}class Solution {
private:
bool ok = true;
vector<bool> color;
vector<bool> visited;
public:
bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
// 图节点编号从 1 开始
color.resize(n + 1);
visited.resize(n + 1);
// 转化成邻接表表示图结构
vector<vector<int>> graph = buildGraph(n, dislikes);
for (int v = 1; v <= n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
}
private:
// 建图函数
vector<vector<int>> buildGraph(int n, vector<vector<int>>& dislikes) {
// 图节点编号为 1...n
vector<vector<int>> graph(n + 1);
for (const auto& edge : dislikes) {
int v = edge[1];
int w = edge[0];
// 「无向图」相当于「双向图」
// v -> w
graph[v].push_back(w);
// w -> v
graph[w].push_back(v);
}
return graph;
}
// 和之前判定二分图的 traverse 函数完全相同
void traverse(const vector<vector<int>>& graph, int v) {
if (!ok) return;
visited[v] = true;
for (int w : graph[v]) {
if (!visited[w]) {
color[w] = !color[v];
traverse(graph, w);
} else {
if (color[w] == color[v]) {
ok = false;
}
}
}
}
};class Solution:
def __init__(self):
self.ok = True
self.color = None
self.visited = None
def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:
# 图节点编号从 1 开始
self.color = [False] * (n + 1)
self.visited = [False] * (n + 1)
# 转化成邻接表表示图结构
graph = self.buildGraph(n, dislikes)
for v in range(1, n + 1):
if not self.visited[v]:
self.traverse(graph, v)
return self.ok
# 建图函数
def buildGraph(self, n: int, dislikes: List[List[int]]) -> List[List[int]]:
# 图节点编号为 1...n
graph = [[] for _ in range(n + 1)]
for edge in dislikes:
v = edge[1]
w = edge[0]
# 「无向图」相当于「双向图」
# v -> w
graph[v].append(w)
# w -> v
graph[w].append(v)
return graph
# 和之前判定二分图的 traverse 函数完全相同
def traverse(self, graph: List[List[int]], v: int):
if not self.ok:
return
self.visited[v] = True
for w in graph[v]:
if not self.visited[w]:
self.color[w] = not self.color[v]
self.traverse(graph, w)
else:
if self.color[w] == self.color[v]:
self.ok = False// possibleBipartition determines if it's possible to bipartition the graph
func possibleBipartition(n int, dislikes [][]int) bool {
// 图节点编号从 1 开始
// 转化成邻接表表示图结构
graph := buildGraph(n, dislikes)
color := make([]bool, n+1)
visited := make([]bool, n+1)
// Try to color the graph
for v := 1; v <= n; v++ {
if !visited[v] {
if !traverse(graph, v, color, visited) {
return false
}
}
}
return true
}
// buildGraph converts the edge list to an adjacency list representation of the graph
// 建图函数
func buildGraph(n int, dislikes [][]int) [][]int {
// 图节点编号为 1...n
graph := make([][]int, n+1)
for i := 1; i <= n; i++ {
graph[i] = make([]int, 0)
}
for _, edge := range dislikes {
v, w := edge[1], edge[0]
// 「无向图」相当于「双向图」
graph[v] = append(graph[v], w)
graph[w] = append(graph[w], v)
}
return graph
}
// traverse performs DFS on the graph to check if it can be colored properly
// 和之前判定二分图的 traverse 函数完全相同
func traverse(graph [][]int, v int, color []bool, visited []bool) bool {
visited[v] = true
for _, w := range graph[v] {
if !visited[w] {
color[w] = !color[v]
if !traverse(graph, w, color, visited) {
return false
}
} else if color[w] == color[v] {
return false
}
}
return true
}var possibleBipartition = function(n, dislikes) {
let ok = true;
let color = new Array(n + 1).fill(false);
let visited = new Array(n + 1).fill(false);
// 图节点编号从 1 开始
// 转化成邻接表表示图结构
let graph = buildGraph(n, dislikes);
for (let v = 1; v <= n; v++) {
if (!visited[v]) {
traverse(graph, v);
}
}
return ok;
// 建图函数
function buildGraph(n, dislikes) {
// 图节点编号为 1...n
let graph = new Array(n + 1).fill(0).map(() => []);
for (let i = 1; i <= n; i++) {
graph[i] = [];
}
for (let edge of dislikes) {
let v = edge[1];
let w = edge[0];
// 「无向图」相当于「双向图」
// v -> w
graph[v].push(w);
// w -> v
graph[w].push(v);
}
return graph;
}
// 和之前判定二分图的 traverse 函数完全相同
function traverse(graph, v) {
if (!ok) return;
visited[v] = true;
for (let w of graph[v]) {
if (!visited[w]) {
color[w] = !color[v];
traverse(graph, w);
} else {
if (color[w] == color[v]) {
ok = false;
}
}
}
}
};算法可视化面板
至此,这道题也使用 DFS 算法解决了,如果你想用 BFS 算法,和之前写的解法是类似的,在扩散的时候,尝试对相邻元素颜色就行了,你可以自己尝试实现。