Union Find 并查集原理

本文将介绍什么是图的动态连通性问题，以及为什么并查集（Union Find）算法能够高效解决动态连通性问题。

本文会结合 可视化面板 直观展示 Union Find 算法的核心原理，以及几种优化思路的效果。

考虑到这是基础章节，本文不涉及算法代码的实现细节。具体的代码实现和算法题的运用放在后面的 Union Find 算法实现及应用 和 并查集经典习题 章节中，建议初学者按照目录顺序循序渐进地学习。

动态连通性及术语

图论算法中专业术语比较多，我就用一个简单的例子来介绍几个专业术语。

比如下面这个例子，其中有 10 个节点，分别用 0~9 标记，虽然其中没有边，但它依然是一个图结构：

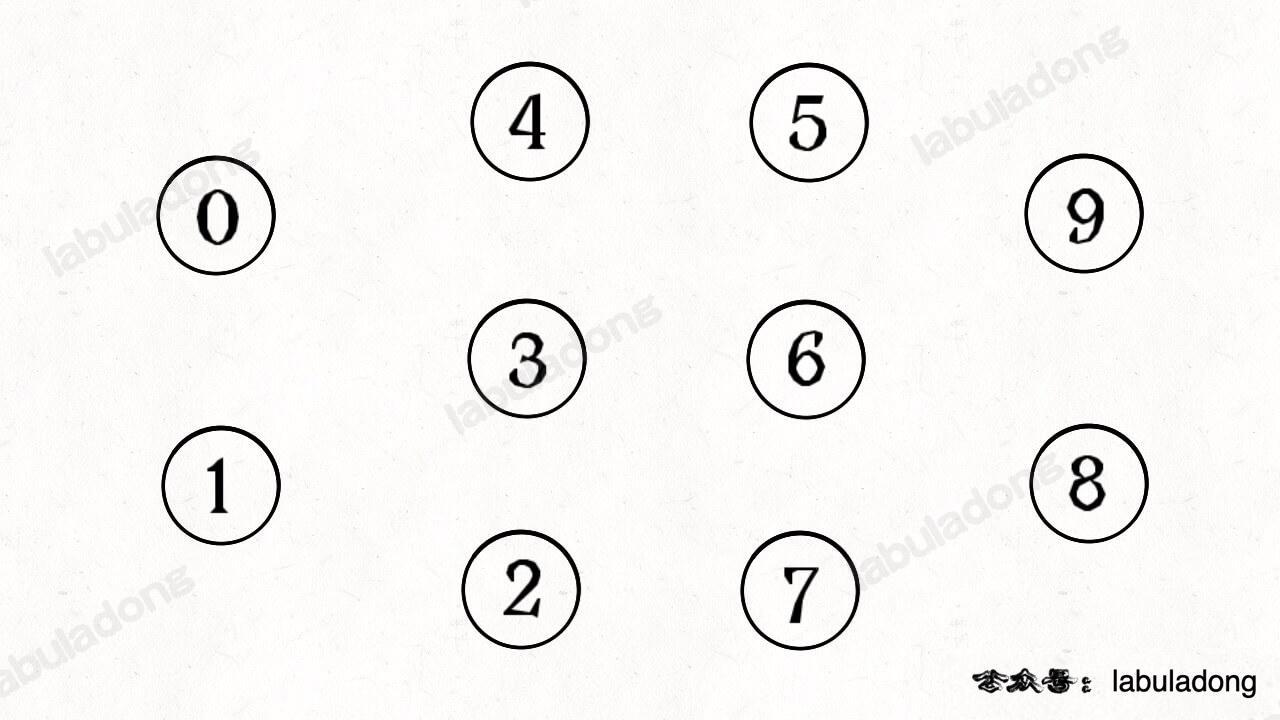
我们可以说这个图结构中，有 10 个「连通分量」，每个节点自身都是一个连通分量，因为它们自成一派，没有和其他节点相连。

现在将其中的一些节点进行「连接操作」，比如连接节点 0,1 和 1,2：

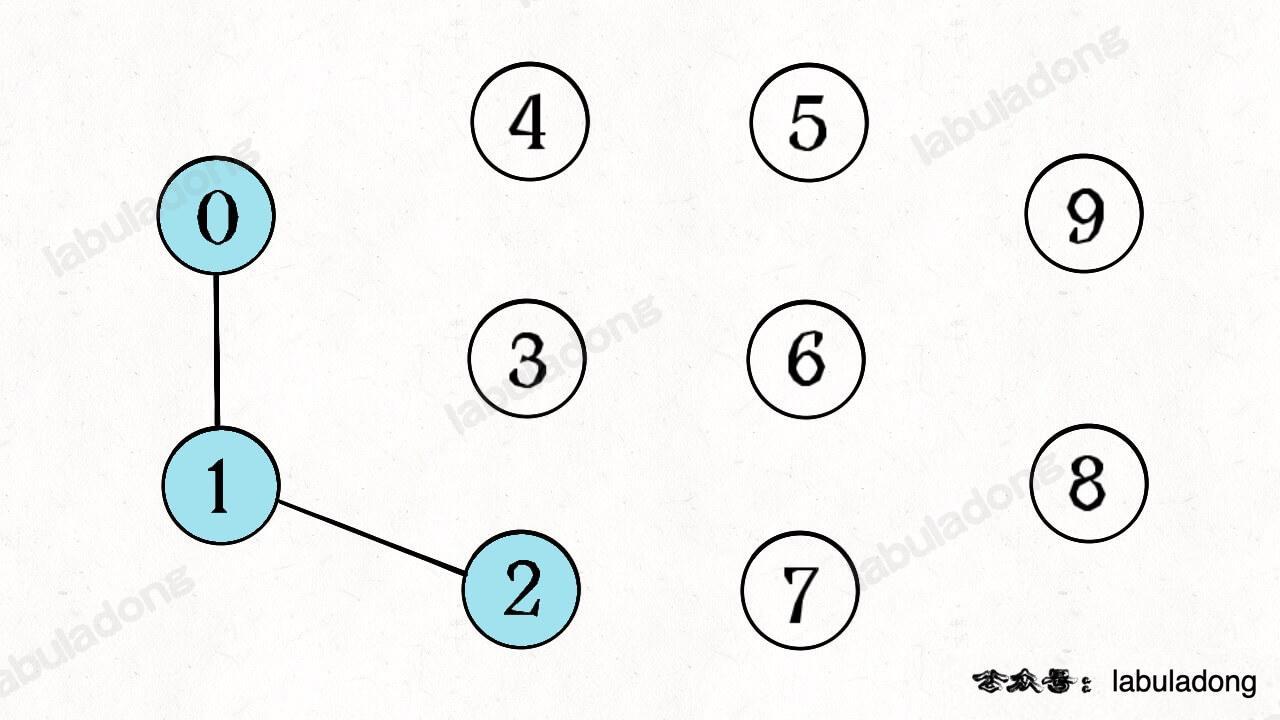
此时，图结构中的节点 0,1,2 之间就连通了，它们三个节点共同构成了一个连通分量，我们可以说这三个节点是「连通」的。

同时，这个图结构中的连通分量的数量从 10 减少到了 8，因为连接操作将 0,1,2 三个连通分量合并成了一个。

那么动态连通性问题就是说，给你输入一个图结构，然后进行若干次「连接操作」，同时可能会查询任意两个节点是否「连通」，或者查询当前图中有多少个「连通分量」。

我们的目标是设计一种数据结构，在尽可能小的时间复杂度下完成连接操作和查询操作。

为什么需要并查集算法

并查集（Union Find）结构提供如下 API：

class UF {
    // 初始化并查集，包含 n 个节点，时间复杂度 O(n)
    public UF(int n);

    // 连接节点 p 和节点 q，时间复杂度 O(1)
    public void union(int p, int q);

    // 查询节点 p 和节点 q 是否连通（是否在同一个连通分量内），时间复杂度 O(1)
    public boolean connected(int p, int q);

    // 查询当前的连通分量数量，时间复杂度 O(1)
    public int count();
}

其中 union 方法用于连接两个节点，connected 方法用于查询两个节点是否连通，count 方法用于查询当前图中的连通分量数量。它们都可以在 $O(1)$ 时间内完成。

$O(1)$ 的时间复杂度是最牛逼的，假设你没学过并查集算法，你应该如何实现上述几个方法呢？

也不是完全没办法，比如 图结构基础及通用代码实现 中已经介绍了图结构邻接表/邻接矩阵的代码实现，这个 union 方法其实就是在图中添加一条无向边，时间复杂度可以做到 $O(1)$。

这个 connected 方法怎么实现呢？你是不是想说，去查一下邻接表/邻接矩阵，看看这两个节点是否相连就行了？

不对，别忘了上面讲的「连通」的性质，其中有有一条是「传递性」：如果节点 p 和 q 连通，q 和 r 连通，那么 p 和 r 也连通。

你单纯去查邻接表/邻接矩阵，只能判断两个节点是否直接相连，而无法处理这种传递的连通关系。

所以，要想实现 connected(a, b)，我们只能使用 图结构的 DFS/BFS 遍历算法，从 a 节点开始遍历所有可达的节点，看看 b 节点是否在其中，才能判断 a,b 两个节点是否连通。

这样的话，connected 方法的最坏时间复杂度就是图遍历的复杂度 $O(V+E)$，其中 $V$ 是节点数量，$E$ 是边数量。

接下来，count 方法如何实现呢？

还得依赖 图结构的 DFS/BFS 遍历算法，但是更麻烦。

你得用 BFS/DFS 遍历整幅图，将所有节点分类到不同的连通分量中，最后统计连通分量的数量。这个过程的时间复杂度是 $O(V+E)$。

所以说并查集算法非常巧妙，它不仅可以在 $O(1)$ 时间内完成上述操作，而且它根本不需要真的用邻接表/邻接矩阵构造图结构，只需要一个数组就可以了。

下面具体介绍。