用数组加强哈希表（ArrayHashMap）

labuladong原创约 2792 字

前置知识

阅读本文前，你需要先学习：

哈希表核心原理

上一章用链表加强哈希表我们利用双链表对哈希表进行了加强，实现了 LinkedHashMap 这种数据结构，让哈希表的键保持插入顺序。

链表能加强哈希表，数组作为链表的好兄弟，其实也能加强哈希表。

添加 `randomKey()` API

现在我给你出个题，让你基于标准哈希表的 API 之上，再添加一个新的 randomKey() API，可以在 O(1) 的时间复杂度返回一个随机键：

interface Map<K, V> {
    // 获取 key 对应的 value，时间复杂度 O(1)
    V get(K key);

    // 添加/修改 key-value 对，时间复杂度 O(1)
    void put(K key, V value);

    // 删除 key-value 对，时间复杂度 O(1)
    void remove(K key);

    // 是否包含 key，时间复杂度 O(1)
    boolean containsKey(K key);

    // 返回所有 key，时间复杂度 O(N)
    List<K> keys();

    // 新增 API：随机返回一个 key，要求时间复杂度 O(1)
    K randomKey();
}

均匀随机（uniform random）

注意，我们一般说的随机，都是指均匀随机，即每个元素被选中的概率相等。比如你有 n 个元素，你的随机算法要保证每个元素被选中的概率都是 1/n，才叫均匀随机。

怎么样，你会不会做？不要小看这个简单的需求，实现方法其实是比较巧妙的。

通过前面的学习，你应该知道哈希表的本质就是一个 table 数组，现在让你随机返回一个哈希表的键，很容易就会联想到在数组中随机获取一个元素。

在标准数组，随机获取一个元素很简单，只要用随机数生成器生成一个 [0, size) 的随机索引，就相当于找了一个随机元素：

java 🟢

int randomeElement(int[] arr) {
    Random r = new Random();
    // 生成 [0, arr.length) 的随机索引
    return arr[r.nextInt(arr.length)];
}

cpp 🤖

int randomeElement(vector<int>& arr) {
    // 生成 [0, arr.size()) 的随机索引
    return arr[rand() % arr.size()];
}

python 🤖

import random

def randomeElement(arr: List[int]) -> int:
    # 生成 [0, len(arr)) 的随机索引
    return arr[random.randint(0, len(arr) - 1)]

go 🤖

import "math/rand"

func randomeElement(arr []int) int {
    // 生成 [0, len(arr)) 的随机索引
    return arr[rand.Intn(len(arr))]
}

javascript 🤖

function randomeElement(arr) {
    // 生成 [0, arr.length) 的随机索引
    return arr[Math.floor(Math.random() * arr.length)];
}

这个算法是正确的，它的复杂度是 O(1)，且每个元素被选中的概率都是 1/n，n 为 arr 数组的总元素个数。

但你注意，上面这个函数有个前提，就是数组中的元素是紧凑存储没有空洞的，比如 arr = [1, 2, 3, 4]，这样才能保证任意一个随机索引都对应一个有效的元素。

如果数组中有空洞就有问题了，比如 arr = [1, 2, null, 4]，其中 arr[2] = null 代表没有存储元素的空洞，那么如果你生成的随机数恰好是 2，请问你该怎么办？

也许你想说，可以向左或者向右线性查找，找到一个非空的元素返回，类似这样：

// 返回一个非空的随机元素（伪码）
int randomeElement(int[] arr) {
    Random r = new Random();
    // 生成 [0, arr.length) 的随机索引
    int i = r.nextInt(arr.length);
    while (arr[i] == null) {
        // 随机生成的索引 i 恰巧是空洞
        // 借助环形数组技巧向右进行探查
        // 直到找到一个非空元素
        i = (i + 1) % arr.length;
    }
    return arr[i];
}

你这样是不行的，这个算法有两个问题：

1、有个循环，最坏时间复杂度上升到了 O(N)，不符合 O(1) 的要求。

2、这个算法不是均匀随机的，因为你的查找方向是固定的，空洞右侧的元素被选中的概率会更大。比如 arr = [1, 2, null, 4]，元素 1, 2, 4 被选中的概率分别是 1/4, 1/4, 2/4。

那也许还有个办法，一次运气不好，就多来随机几次，直到找到一个非空元素：

// 返回一个非空的随机元素（伪码）
int randomeElement(int[] arr) {
    Random r = new Random();
    // 生成 [0, arr.length) 的随机索引
    int i = r.nextInt(arr.length);
    while (arr[i] == null) {
        // 随机生成的索引 i 恰巧是空洞
        // 重新生成一个随机索引
        i = r.nextInt(arr.length);
    }
    return arr[i];
}

现在这个算法是均匀随机的，但问题也非常明显，它的时间复杂度竟然依赖随机数！肯定不是 O(1) 的，不符合要求。

怎么样，从一个带有空洞的数组中随机返回一个元素是不是都把你难住了？

别忘了，我们现在的目标是从哈希表中随机返回一个键，哈希表底层的 table 数组不仅包含空洞，情况还会更复杂一些：

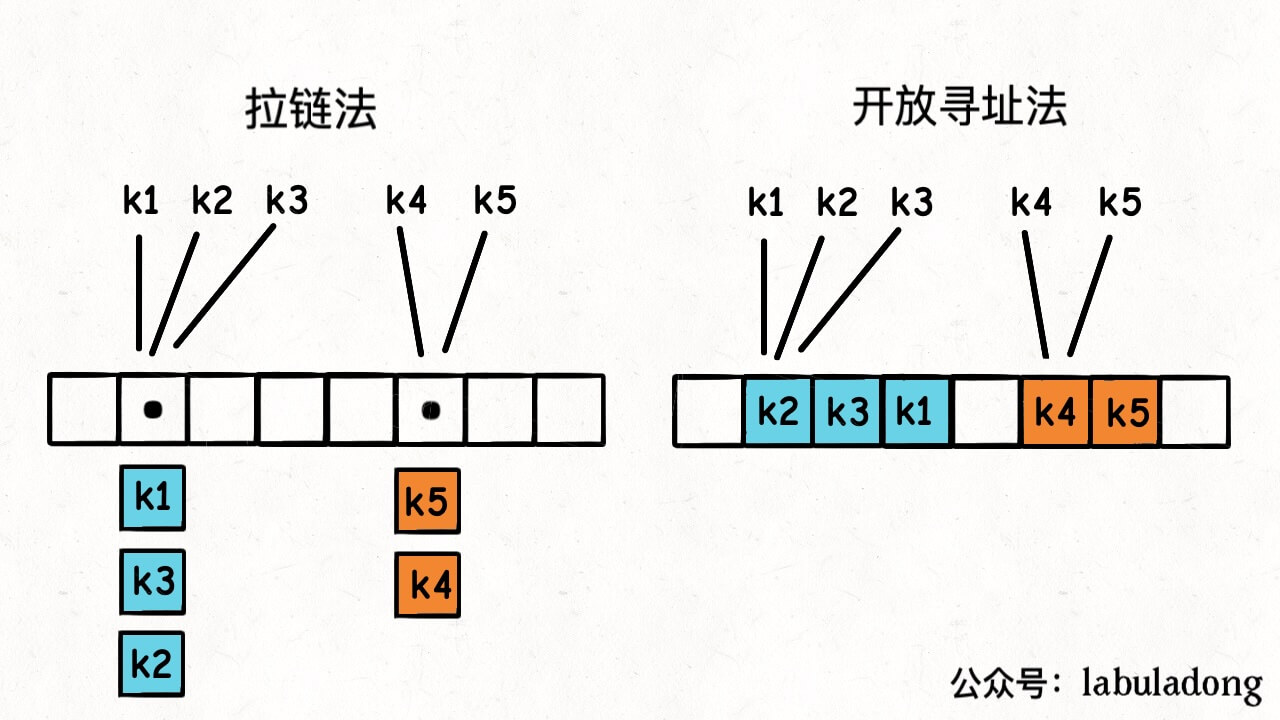
如果你的哈希表用开放寻址法解决哈希冲突，那还好，就是带空洞数组的场景。

如果你的哈希表用拉链法，那可麻烦了。数组里面的每个元素是一个链表，你光随机一个索引是不够的，还要随机链表中的一个节点。

而且注意概率，这个拉链法，就算你均匀随机到一个数组索引，又均匀随机该索引存储的链表节点，得到的这个键是均匀随机的么？

其实不是，上图中 k1, k2, k3 被随机到的概率是 1/2 * 1/3 = 1/6，而 k4, k5 被随机到的概率是 1/2 * 1/2 = 1/4，这不是均匀随机。

关于概率算法

概率算法也是非常有意思的一类问题，无论算法题还是实际业务中都会用到一些经典的随机算法，我会在后文谈谈游戏中的随机算法和带权重的随机选择中详细讲解，这里暂时不需要掌握。

唯一的办法就是通过 keys 方法遍历整个 table 数组，把所有的键都存储到一个数组中，然后再随机返回一个键。但这样复杂度就是 O(N) 了，还是不符合要求。

是不是感觉已经走投无路了？所以说，还是要积累一些经典数据结构设计经验，如果面试笔试的时候遇到类似的问题，你现场想恐怕是很难的。下面我就来介绍一下如何用数组加强哈希表，轻松实现 randomKey() API。

用数组加强哈希表（ArrayHashMap）

添加 `randomKey()` API

实现思路

代码实现

用数组加强哈希表（ArrayHashMap）

添加 randomKey() API

实现思路

代码实现

添加 `randomKey()` API