哈希表核心原理

首先，我需要先阐明一个初学者很容易犯的概念错误。

请问，哈希表和我们常说的 Map（键值映射）是不是同一个东西？不是。

这一点用 Java 来讲解就很清楚，Map 是一个 Java 接口，仅仅声明了若干个方法，并没有给出方法的具体实现：

interface Map<K, V> {
    V get(K key);
    void put(K key, V value);
    V remove(K key);
    // ...
}

Map 接口本身只定义了键值映射的一系列操作，HashMap 这种数据结构根据自身特点实现了这些操作。还有其他数据结构也实现了这个接口，比如 TreeMap、LinkedHashMap 等等。

换句话说，你可以说 HashMap 的 get, put, remove 方法的复杂度都是 $O(1)$ 的，但你不能说 Map 接口的复杂度都是 $O(1)$。因为如果换成其他的实现类，比如底层用二叉树结构实现的 TreeMap，这些方法的复杂度就变成 $O(logN)$ 了。

我为什么要强调这一点呢？主要是针对使用非 Java 语言的读者。

其他编程语言可能没有 Java 这么清晰的接口定义，所以很容易让读者把哈希表和 Map 键值对混为一谈，听到键值对操作，就认为其增删查改的复杂度一定是 $O(1)$。这是不对的，具体要看这个底层的数据结构是如何实现键值操作的。

那么这一章节我会带大家动手实现一个哈希表，探讨哈希表为什么能做到增删查改 $O(1)$ 复杂度，以及解决哈希冲突的两种办法。

哈希表的基本原理

// 哈希表伪码逻辑
class MyHashMap {

    private Object[] table;

    // 增/改，复杂度 O(1)
    public void put(K key, V value) {
        int index = hash(key);
        table[index] = value;
    }

    // 查，复杂度 O(1)
    public V get(K key) {
        int index = hash(key);
        return table[index];
    }

    // 删，复杂度 O(1)
    public void remove(K key) {
        int index = hash(key);
        table[index] = null;
    }

    // 哈希函数，把 key 转化成 table 中的合法索引
    // 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
    private int hash(K key) {
        // ...
    }
}

// 哈希表伪码逻辑
class MyHashMap {

private:
    vector<void*> table;

public:
    // 增/改，复杂度 O(1)
    void put(auto key, auto value) {
        int index = hash(key);
        table[index] = value;
    }

    // 查，复杂度 O(1)
    auto get(auto key) {
        int index = hash(key);
        return table[index];
    }

    // 删，复杂度 O(1)
    void remove(auto key) {
        int index = hash(key);
        table[index] = nullptr;
    }

private:
    // 哈希函数，把 key 转化成 table 中的合法索引
    // 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
    int hash(auto key) {
        // ...
    }
};

# 哈希表伪码逻辑
class MyHashMap:

    def __init__(self):
        self.table = [None] * 1000

    # 增/改，复杂度 O(1)
    def put(self, key, value):
        index = self.hash(key)
        self.table[index] = value

    # 查，复杂度 O(1)
    def get(self, key):
        index = self.hash(key)
        return self.table[index]

    # 删，复杂度 O(1)
    def remove(self, key):
        index = self.hash(key)
        self.table[index] = None

    # 哈希函数，把 key 转化成 table 中的合法索引
    # 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
    def hash(self, key):
        # ...
        pass

// 哈希表伪码逻辑
type MyHashMap struct {
	table []interface{}
}

func Constructor() MyHashMap {
	return MyHashMap{
		table: make([]interface{}, 10000),
	}
}

// 增/改，复杂度 O(1)
func (h *MyHashMap) Put(key, value interface{}) {
	index := h.hash(key)
	h.table[index] = value
}

// 查，复杂度 O(1)
func (h *MyHashMap) Get(key interface{}) interface{} {
	index := h.hash(key)
	return h.table[index]
}

// 删，复杂度 O(1)
func (h *MyHashMap) Remove(key interface{}) {
	index := h.hash(key)
	h.table[index] = nil
}

// 哈希函数，把 key 转化成 table 中的合法索引
// 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
func (h *MyHashMap) hash(key interface{}) int {
	...
}

// 哈希表伪码逻辑
class MyHashMap {
    constructor() {
        this.table = new Array(1000).fill(null);
    }

    // 增/改，复杂度 O(1)
    put(key, value) {
        const index = this.hash(key);
        this.table[index] = value;
    }

    // 查，复杂度 O(1)
    get(key) {
        const index = this.hash(key);
        return this.table[index];
    }

    // 删，复杂度 O(1)
    remove(key) {
        const index = this.hash(key);
        this.table[index] = null;
    }

    // 哈希函数，把 key 转化成 table 中的合法索引
    // 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
    hash(key) {
        // ...
    }
}

几个关键概念及原理

key 是唯一的，value 可以重复

哈希表中，不可能出现两个相同的 key，而 value 是可以重复的。

明白了上面讲的原理应该很好理解，你直接类比数组就行了：

数组里面每个索引都是唯一的，不可能说你这个数组有两个索引 0。至于数组里面存什么元素，随便你，没人 care。

所以哈希表是一样的，key 的值不可能出现重复，而 value 的值可以随意。

哈希函数

哈希函数的作用是把任意长度的输入（key）转化成固定长度的输出（索引）。

你也看到了，增删查改的方法中都会用到哈希函数来计算索引，如果你设计的这个哈希函数复杂度是 $O(N)$，那么哈希表的增删查改性能就会退化成 $O(N)$，所以说这个函数的性能很关键。

这个函数还要保证的一点是，输入相同的 key，输出也必须要相同，这样才能保证哈希表的正确性。不能说现在你计算 hash("123") = 5，待会儿计算 hash("123") = 6，这样的话哈希表就废了。

那么哈希函数是如何把非整数类型的 key 转化成整数索引的？又是如何保证这个索引是合法的呢？

int h = key.hashCode();
if (h < 0) h = -h;

int h = key.hashCode();
// 位运算，把最高位的符号位去掉
// 另外，位运算的运行速度也会比一般的算术运算快
// 所以你看标准库的源码，能用位运算的地方它都会优先使用位运算
h = h & 0x7fffffff;
// 这个 0x7fffffff 的二进制表示是 0111 1111 ... 1111
// 即除了最高位（符号位）是 0，其他位都是 1
// 把 0x7fffffff 和其他 int 进行 & 运算之后，最高位（符号位）就会被清零，即保证了 h 是非负数

int hash(K key) {
    int h = key.hashCode();
    // 保证非负数
    h = h & 0x7fffffff;
    // 映射到 table 数组的合法索引
    return h % table.length;
}

哈希冲突

上面给出了 hash 函数的实现，那么你肯定也会想到，如果两个不同的 key 通过哈希函数得到了相同的索引，怎么办呢？这种情况就叫做「哈希冲突」。

出现哈希冲突的情况怎么解决？两种常见的解决方法，一种是拉链法，另一种是线性探查法（也经常被叫做开放寻址法）。

名字听起来高大上，说白了就是纵向延伸和横向延伸两种思路嘛：

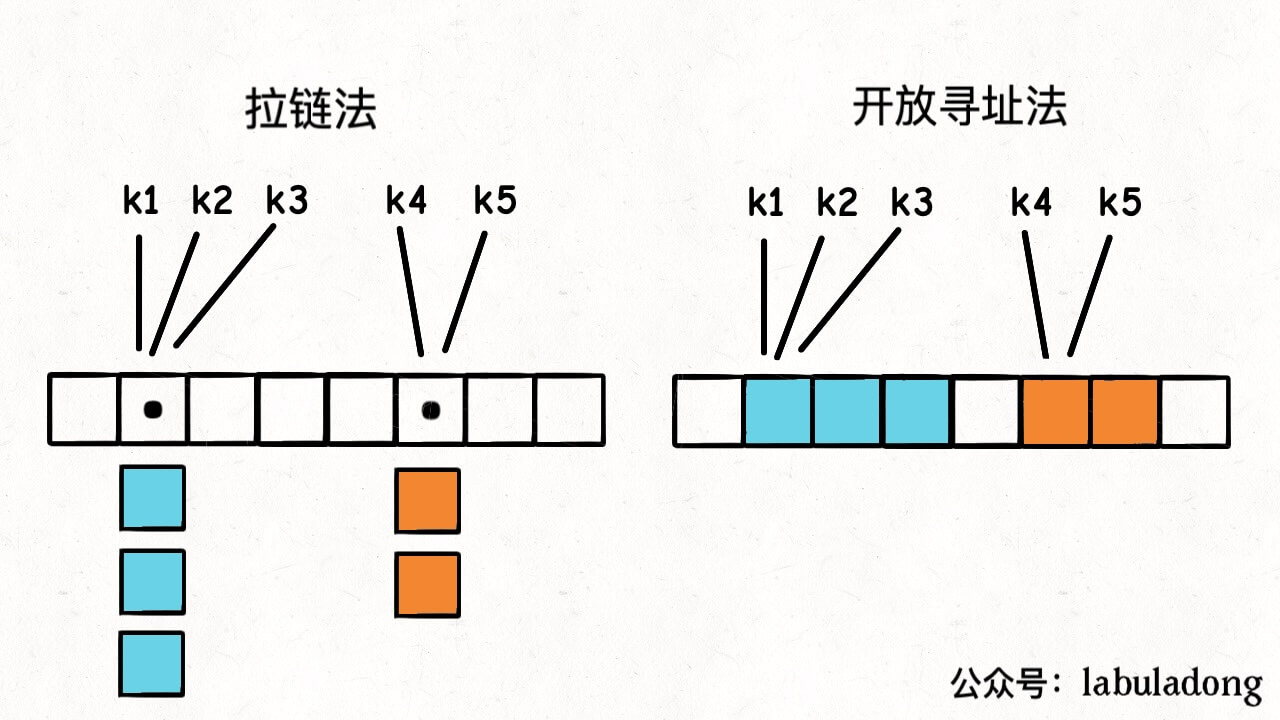
拉链法相当于是哈希表的底层数组并不直接存储 value 类型，而是存储一个链表，当有多个不同的 key 映射到了同一个索引上，这些 key -> value 对儿就存储在这个链表中，这样就能解决哈希冲突的问题。

而线性探查法的思路是，一个 key 发现算出来的 index 值已经被别的 key 占了，那么它就去 index + 1 的位置看看，如果还是被占了，就继续往后找，直到找到一个空的位置为止。

比方说上图，key 的插入顺序是 k2, k4, k5, k3, k1，那么哈希表底层就会变成这样：

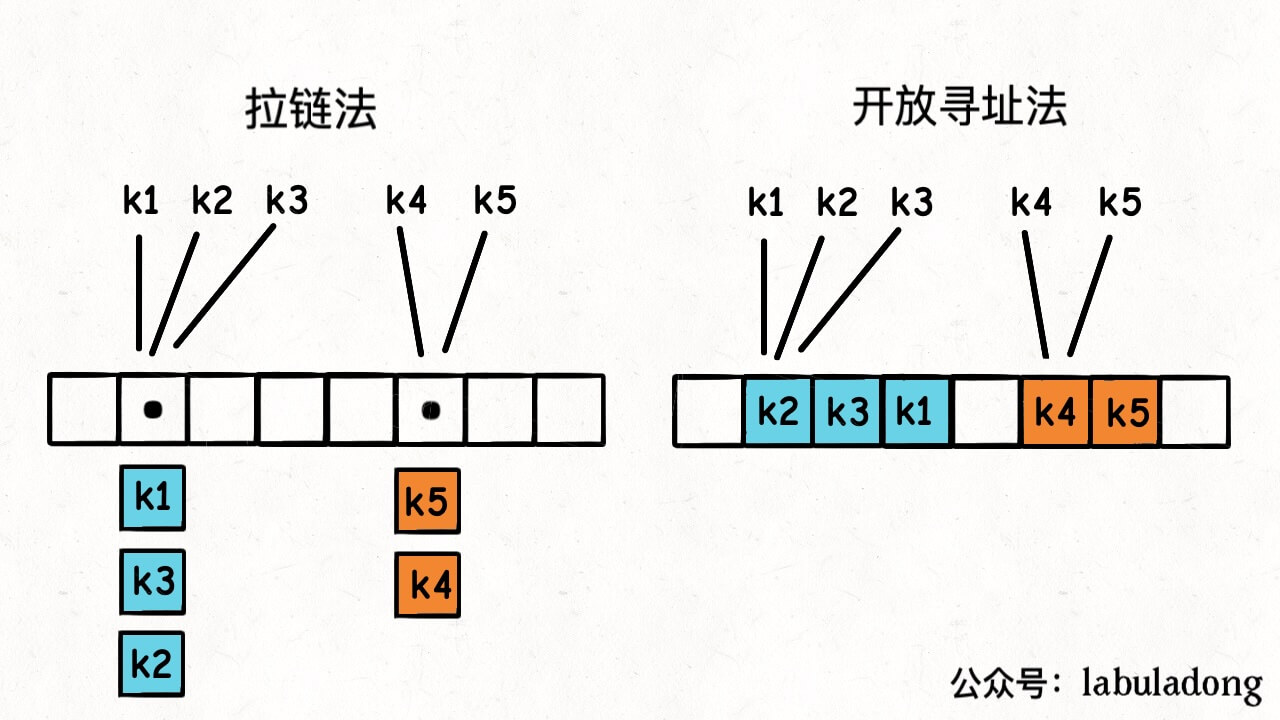
这里先讲一下原理，后面的章节我会手把手带大家分别实现这两种方法来解决哈希冲突。

扩容和负载因子

相信大家都听说过「负载因子」这个专业术语，现在你明白了哈希冲突的问题，就能理解负载因子的意义了。

拉链法和线性探查法虽然能解决哈希冲突的问题，但是它们会导致性能下降。

比如拉链法，你算出来 index = hash(key) 这个索引了，结果过去查出来的是个链表，你还得遍历一下这个链表，才能在里面找到你要的 value。这个过程的时间复杂度是 $O(K)$，K 是这个链表的长度。

线性探查法也是类似的，你算出来 index = hash(key) 这个索引了，你去这个索引位置查看，发现存储的不是要找的 key，但由于线性探查法解决哈希冲突的方式，你并不能确定这个 key 真的不存在，你必须顺着这个索引往后找，直到找到一个空的位置或者找到这个 key 为止，这个过程的时间复杂度也是 $O(K)$，K 为连续探查的次数。

所以说，如果频繁出现哈希冲突，那么 K 的值就会增大，这个哈希表的性能就会显著下降。这是我们需要避免的。

那么为什么会频繁出现哈希冲突呢？两个原因呗：

1、哈希函数设计的不好，导致 key 的哈希值分布不均匀，很多 key 映射到了同一个索引上。

2、哈希表里面已经装了太多的 key-value 对了，这种情况下即使哈希函数再完美，也没办法避免哈希冲突。

对于第一个问题没什么好说的，开发编程语言标准库的大佬们已经帮你设计好了哈希函数，你只要调用就行了。

对于第二个问题是我们可以控制的，即避免哈希表装太满，这就引出了「负载因子」的概念。

为什么不能依赖哈希表的遍历顺序

你大概也听过一个编程常识，即哈希表中键的遍历顺序是无序的，不能依赖哈希表的遍历顺序来编写程序。这是为什么呢？

哈希表的遍历本质上就是遍历那个底层 table 数组：

// 遍历所有 key 的伪码逻辑

// 哈希表底层的 table 数组
KVNode[] table = new KVNode[1000];

// 获取哈希表中的所有键
// 我们不能依赖这个 keys 列表的顺序
List<KeyType> keys = new ArrayList<>();

for (int i = 0; i < table.length; i++) {
    KVNode node = table[i];
    if (node != null) {
        keys.add(node.key);
    }
}

你如果理解了前面讲的内容，应该已经能够理解这个问题了。

首先，由于 hash 函数要把你的 key 进行映射，所以 key 在底层 table 数组中的分布是随机的，不像数组/链表结构那样有个明确的元素顺序。

其次，刚才讲了哈希表达到负载因子时会怎样？会扩容对吧，也就是 table.length 会变化，且会搬移元素。

那么这个搬移数据的过程，是不是要用 hash 函数重新计算 key 的哈希值，然后放到新的 table 数组中？

而这个 hash 函数，它计算出的值依赖 table.length。也就是说，哈希表自动扩容后，同一个 key 的哈希值可能变化，即这个 key-value 对儿存储在 table 的索引也变了，所以遍历结果的顺序就和之前不一样了。

你观察到的现象就是，这次遍历的第一个键是 key1，但是增删几个元素再遍历，可能发现 key1 跑到最后去了。

所以说，这些东西没必要背的，原理搞明白了，你稍微推理下自己都能想通。

为什么不建议在 for 循环中增/删哈希表的 key

注意我这里说的是不建议，并不是一定不可以。因为不同的编程语言标准库对哈希表的实现不同，有些语言针对这种情况做了优化，所以到底行不行，要查阅文档。

我们这里仅从哈希表的原理上分析，在 for 循环中增/删哈希表的 key，是很容易出现问题的，原因和上面相同，还是扩缩容导致的哈希值变化。

遍历哈希表的 key，本质就是遍历哈希表底层的 table 数组，如果一边遍历一边增删元素，如果遍历到一半，插入/删除操作触发了扩缩容，整个 table 数组都变了，那么请问，接下来应该是什么行为？还有，在遍历过程中新插入/删除的元素，是否应该被遍历到？

扩缩容导致 key 顺序变化是哈希表的特有行为，但即便排除这个因素，任何其他数据结构，也都不建议在遍历的过程中同时进行增删，否则很容易导致非预期的行为。

如果你非要这样做，请确保查阅了相关文档，明确这个操作的行为是什么，做到心里有数。

key 必须是不可变的

只有那些不可变类型，才能作为哈希表的 key，这一点很重要。

所谓不可变类型，就是说这个对象一旦创建，它的值就不能再改变了。比如 Java 中的 String, Integer 等类型，一旦创建了这些对象，你就只能读取它的值，而不能再修改它的值了。

作为对比，Java 中的 ArrayList、LinkedList 这些对象，它们创建出来之后，可以往里面随意增删元素，所以它们是可变类型。

因此，你可以把 String 对象作为哈希表的 key，但不能把 ArrayList 对象作为哈希表的 key：

// 可以把不可变类型作为 key
Map<String, AnyOtherType> map1 = new HashMap<>();
Map<Integer, AnyOtherType> map2 = new HashMap<>();

// 不应该把可变类型作为 key
// 注意，这样写并不会产生语法错误，但是代码非常容易出 bug
Map<ArrayList<Integer>, AnyOtherType> map3 = new HashMap<>();

为啥不建议把可变类型作为 key 呢？就比如这个 ArrayList 吧，它的 hashCode 方法的实现逻辑如下：

public int hashCode() {
    for (int i = 0; i < elementData.length; i++) {
        h = 31 * h + elementData[i];
    }
}

第一个就是效率问题，每次计算 hashCode 都要遍历整个数组，复杂度是 $O(N)$，这样就会导致哈希表的增删查改操作的复杂度退化成 $O(N)$。

更严重的问题是，ArrayList 的 hashCode 是根据它里面的元素计算出来的，如果你往这个 ArrayList 里面增删元素，或者其中某个元素的 hashCode 值发生改变，那么这个 ArrayList 的 hashCode 返回值也会发生改变。

比方说，你现在用一个 ArrayList 类型的 arr 变量作为哈希表的 key 在哈希表中保存了对应的 value。但如果 arr 中的某个元素在程序的其他位置被修改了，那么 arr 的 hashCode 就会变化。此时你再用这个 arr 变量去哈希表中查询，发现找不到任何值了。

也就是说，你存入哈希表的 key-value 意外丢失了，这是非常非常严重的 bug，还会带来潜在的内存泄漏问题。

public class Test {
    public static void main(String[] args) {
        // 错误示例
        // 把可变类型作为 HashMap 的 key
        Map<ArrayList<Integer>, Integer> map = new HashMap<>();

        ArrayList<Integer> arr = new ArrayList<>();
        arr.add(1);
        arr.add(2);

        map.put(arr, 999);
        System.out.println(map.containsKey(arr)); // true
        System.out.println(map.get(arr)); // 999

        arr.add(3);
        // 出现严重 bug，键值对丢失
        System.out.println(map.containsKey(arr)); // false
        System.out.println(map.get(arr)); // null

        // 此时 map 底层的 table 中，arr 的键值对数据依然存在
        // 但是由于 arr 的 hashCode 改变了，此键值对无法被查找到
        // 这也会导致内存泄漏，因为这个 arr 变量被 map 引用着，无法被垃圾回收
    }
}

上面就是一个简单的错误示例。你也许会说，把元素 3 删掉，arr -> 999 这个键值对不就又出现了？或者，直接遍历哈希表底层的 table 数组，应该也可以看到这个键值对。

拜托🙏🏻，你这是在写代码还是在写盗墓笔记呢？一会儿出现一会儿消失，你这个哈希表是幽灵附体了吗？

开个玩笑。实际上可变类型本身就是一种不确定性，在代码构成的屎山里，你怎么知道这个 arr 传递到哪里被修改了呢？

所以正确的做法是，使用不可变类型作为哈希表的 key，比方说用 String 类型作为 key。因为 Java 中的 String 对象一旦创建出来，它的值就不允许被改变，你就不会遇到上面的问题。

String 类型的 hashCode 方法也需要遍历所有字符，但是由于它的不可变性，这个值只要算出来一次，就可以缓存下来，不用每次都重新计算，所以 平均时间复杂度 依然是 $O(1)$。

我这里是用 Java 举的例子，其他语言也是类似的，你需要查询相关文档，了解标准库提供的哈希表是如何计算对象哈希值的，避免产生类似的问题。

总结

上面的说明应该已经吧哈希表的底层原理全部串起来了，最后模拟几个面试问题来总结一下本文的内容：

1、为什么我们常说，哈希表的增删查改效率都是 $O(1)$？

因为哈希表底层就是操作一个数组，其主要的时间复杂度来自于哈希函数计算索引和哈希冲突。只要保证哈希函数的复杂度在 $O(1)$，且合理解决哈希冲突的问题，那么增删查改的复杂度就都是 $O(1)$。

2、哈希表的遍历顺序为什么会变化？

因为哈希表在达到负载因子时会扩容，这个扩容过程会导致哈希表底层的数组容量变化，哈希函数计算出来的索引也会变化，所以哈希表的遍历顺序也会变化。

3、哈希表的增删查改效率一定是 $O(1)$ 吗？

不一定，正如前面分析的，只有哈希函数的复杂度是 $O(1)$，且合理解决哈希冲突的问题，才能保证增删查改的复杂度是 $O(1)$。

哈希冲突好解决，都是有标准答案的。关键是哈希函数的计算复杂度。如果使用了错误的 key 类型，比如前面用 ArrayList 作为 key 的例子，那么哈希表的复杂度就会退化成 $O(N)$。

4、为啥一定要用不可变类型作为哈希表的 key？

因为哈希表的主要操作都依赖于哈希函数计算出来的索引，如果 key 的哈希值会变化，会导致键值对意外丢失，产生严重的 bug。

要对自己使用的编程语言标准库中的源码有一定的了解，才能保证写出高效的代码。

下面，就我将手把手带大家分别用拉链法和线性探查法来实现简单的哈希表，来加深对哈希表的理解。