二叉树的递归/层序遍历

了解了 二叉树基本概念和几种特殊的二叉树，本文来讲解如何遍历和访问二叉树的节点。

二叉树的遍历算法主要分为递归遍历和层序遍历两种，都有代码模板。递归代码模板可以延伸出后面要讲的 DFS 算法、回溯算法，层序代码模板可以延伸出后面要讲的 BFS 算法，所以我经常强调二叉树结构的重要性。

大家熟知的前序遍历、中序遍历、后序遍历，都属于二叉树的递归遍历，只不过是把自定义代码插入到了代码模板的不同位置而已，下面我会结合可视化面板来讲解。

递归遍历（DFS）

递归遍历二叉树的代码模板如下：

// 基本的二叉树节点
class TreeNode {
    int val;
    TreeNode left, right;
}

// 二叉树的递归遍历框架
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

// 基本的二叉树节点
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 二叉树的递归遍历框架
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    traverse(root->left);
    traverse(root->right);
}

# 基本的二叉树节点
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 二叉树的递归遍历框架
def traverse(root: TreeNode):
    if root is None:
        return
    traverse(root.left)
    traverse(root.right)

// 基本的二叉树节点
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

// 二叉树的递归遍历框架
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.Left)
    traverse(root.Right)
}

// 基本的二叉树节点
class TreeNode {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

// 二叉树的递归遍历框架
var traverse = function(root) {
    if (root === null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

请问，这段短小精干的代码为什么能遍历二叉树？又是以什么顺序遍历二叉树的？

对于 traverse 这样的递归遍历函数，你就可以把它理解成一个在二叉树结构上游走的指针，下面用一个可视化面板直观地展现这个算法的遍历过程。

不用着急，你可以多看几遍这个可视化面板，直到把 traverse 函数遍历二叉树的顺序彻底搞清楚为止。

traverse 函数的遍历顺序就是一直往左子节点走，直到遇到空指针不能再走了，才尝试往右子节点走一步；然后再一直尝试往左子节点走，如此循环；如果左右子树都走完了，则返回上一层父节点。

看代码也能看出来，先递归调用的 root.left，然后才递归调用的 root.right，每次进入 traverse 函数，都会先往左子节点递归遍历，直到遇到空指针走不动了，才轮到往右子节点走一次。

那么我们简单拓展一下，如果修改前面的 traverse 函数，先递归遍历 root.right，再递归遍历 root.left，会是什么效果？

// 修改标准的二叉树遍历框架
void traverseFlip(TreeNode root) {
    if (root == null) {
        return;
    }
    // 反过来，先递归遍历右子树，再递归遍历左子树
    traverseFlip(root.right);
    traverseFlip(root.left);
}

可以看到 traverseFlip 函数也能遍历二叉树的所有节点，只不过和标准的 traverse 函数遍历顺序相反。

我举这个 traverseFlip 的例子，是想告诉你：

递归遍历节点的顺序（即上面可视化面板中 root 在树上的移动顺序）仅取决于左右子节点的递归调用顺序，与其他代码无关。

我们说二叉树遍历时，一般不会像 traverseFlip 这样遍历二叉树，默认还是按照先左后右的顺序，所以当我们说二叉树遍历的代码模板时，指的是先左后右的遍历顺序：

// 基本的二叉树节点
class TreeNode {
    int val;
    TreeNode left, right;
}

// 二叉树的递归遍历框架
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

// 基本的二叉树节点
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 二叉树的递归遍历框架
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    traverse(root->left);
    traverse(root->right);
}

# 基本的二叉树节点
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 二叉树的递归遍历框架
def traverse(root: TreeNode):
    if root is None:
        return
    traverse(root.left)
    traverse(root.right)

// 基本的二叉树节点
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

// 二叉树的递归遍历框架
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    traverse(root.Left)
    traverse(root.Right)
}

// 基本的二叉树节点
class TreeNode {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

// 二叉树的递归遍历框架
var traverse = function(root) {
    if (root === null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

只要这个先左后右的调用顺序不变，那么 traverse 函数访问节点的顺序就是固定的，你插入一万行代码进去，也不会变。

有一些数据结构基础的读者可能有点晕了：

不对呀，只要上过大学的数据结构课程，就知道二叉树有前/中/后序三种遍历，会得到三种不同顺序的结果。为啥你这里说递归遍历节点的顺序是固定的呢？

这个问题很好，下面来解答。

理解前/中/后序遍历

递归遍历的顺序，即 traverse 函数访问节点的顺序确实是固定的。正如可视化面板所示，root 指针在树上移动的顺序是固定的：

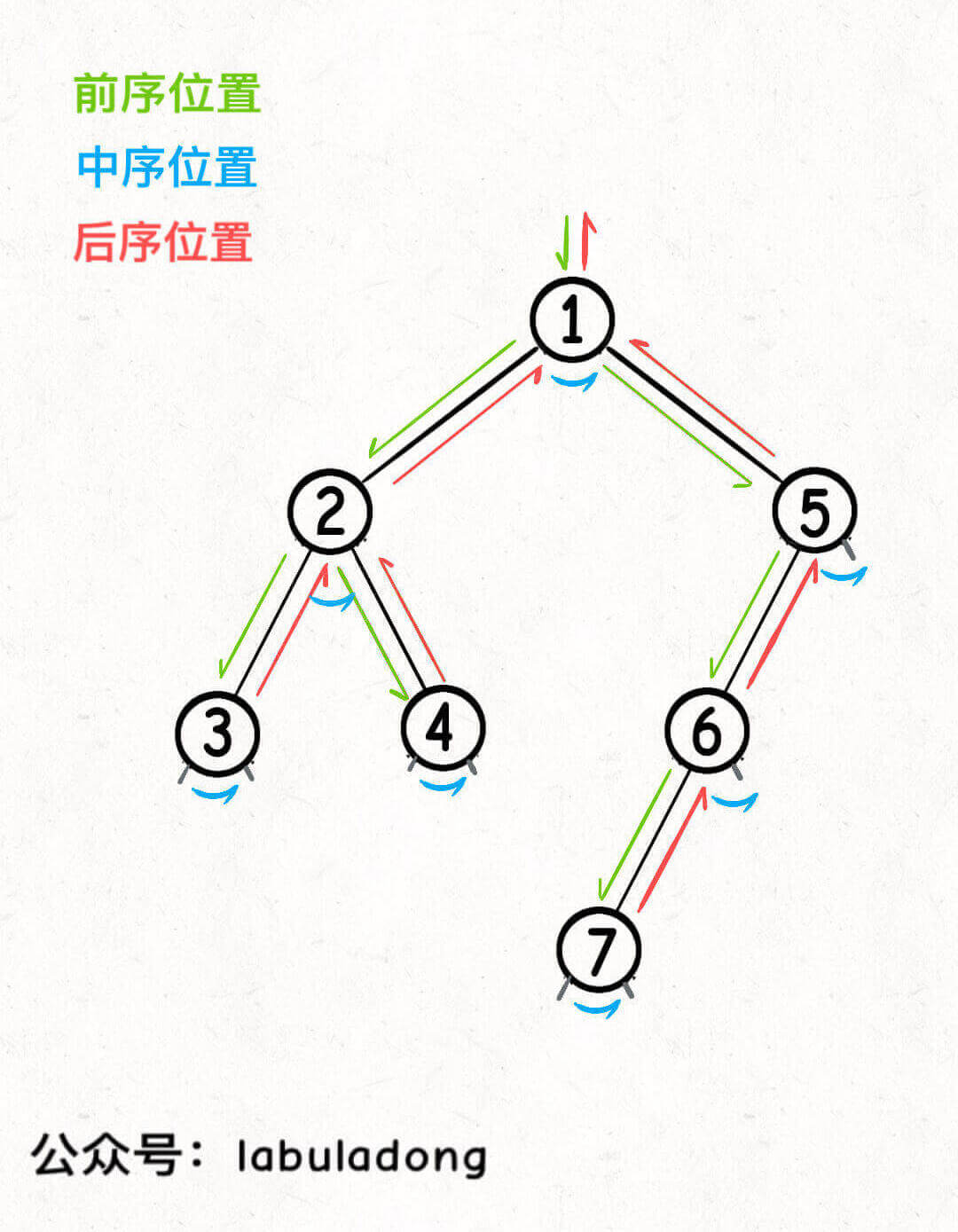
但是，你在 traverse 函数中不同位置写代码，效果是可以不一样的。前中后序遍历的结果不同，原因是因为你把代码写在了不同位置，所以产生了不同的效果。

比方说，刚进入一个节点的时候，你还对它的子节点一无所知，而当你要离开一个节点的时候，它的所有子节点你都遍历过了。那么在这两种情况下写的代码，肯定是可以有不同的效果的。

所谓的前中后序遍历，其实就是在二叉树遍历框架的不同位置写代码：

// 二叉树的遍历框架
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

// 二叉树的遍历框架
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // 前序位置
    traverse(root->left);
    // 中序位置
    traverse(root->right);
    // 后序位置
}

# 二叉树的遍历框架
def traverse(root):
    if root is None:
        return
    # 前序位置
    traverse(root.left)
    # 中序位置
    traverse(root.right)
    # 后序位置

// 二叉树的遍历框架
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // 前序位置
    traverse(root.Left)
    // 中序位置
    traverse(root.Right)
    // 后序位置
}

// 二叉树的遍历框架
var traverse = function(root) {
    if (root === null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
};

前序位置的代码会在进入节点时立即执行；中序位置的代码会在左子树遍历完成后，遍历右子树之前执行；后序位置的代码会在左右子树遍历完成后执行：

下面结合可视化代码就能很直观地理解了。

因为前序位置的代码是刚进入节点时执行的，所以前序遍历的顺序就是 root 指针在树上移动的顺序。

正确理解前中后序位置非常重要，请你仔细理解上面的可视化面板，做到可以心算任意一棵二叉树的前中后序遍历结果。

实际的算法题中不会简单的让你计算前中后序的遍历顺序，而是需要你把正确的代码插入到正确的位置。我会在 二叉树算法思想（纲领篇） 和习题中深入探讨二叉树遍历框架的前中后序位置，以及如何运用到回溯算法、动态规划算法中，这里不展开。

最后一个知识点，二叉搜索树（BST） 的中序遍历结果是有序的，这是 BST 的一个重要性质。

可以看这个可视化面板，点击其中 res.push(root.val); 这一行代码，就可以看到中序遍历访问节点的顺序：

在后续 BST 相关习题集 中，会有一些题目利用到这个特性。

层序遍历（BFS）

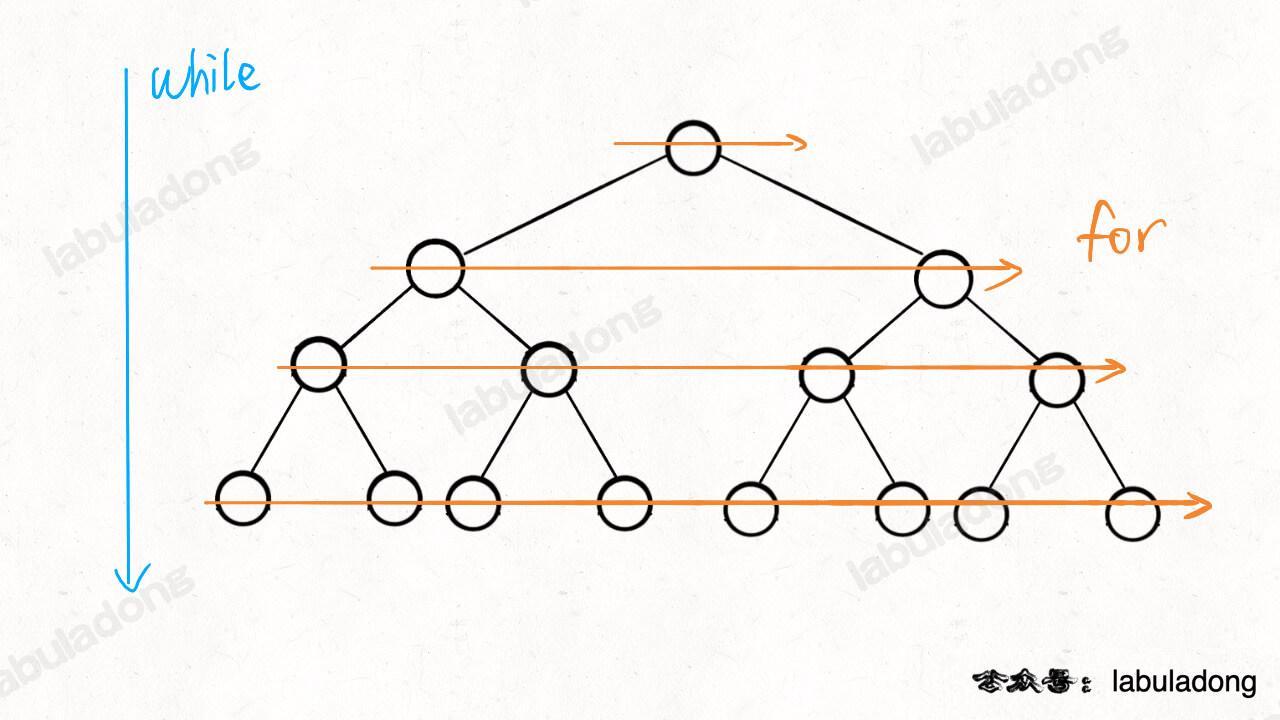
上面讲的递归遍历是依赖函数堆栈递归遍历二叉树的，遍历顺序是从最左侧开始，一列一列地走到最右侧。

二叉树的层序遍历，顾名思义，就是一层一层地遍历二叉树。这个遍历方式需要借助队列来实现，而且根据不同的需求，主要有三种不同的写法，下面一一列举。

写法一

这是最简单的写法，代码如下：

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    while (!q.isEmpty()) {
        TreeNode cur = q.poll();
        // 访问 cur 节点
        System.out.println(cur.val);

        // 把 cur 的左右子节点加入队列
        if (cur.left != null) {
            q.offer(cur.left);
        }
        if (cur.right != null) {
            q.offer(cur.right);
        }
    }
}

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    std::queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* cur = q.front();
        q.pop();
        // 访问 cur 节点
        std::cout << cur->val << std::endl;
        
        // 把 cur 的左右子节点加入队列
        if (cur->left != nullptr) {
            q.push(cur->left);
        }
        if (cur->right != nullptr) {
            q.push(cur->right);
        }
    }
}

from collections import deque

def levelOrderTraverse(root):
    if root is None:
        return
    q = deque()
    q.append(root)
    while q:
        cur = q.popleft()
        # 访问 cur 节点
        print(cur.val)

        # 把 cur 的左右子节点加入队列
        if cur.left is not None:
            q.append(cur.left)
        if cur.right is not None:
            q.append(cur.right)

func levelOrderTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []*TreeNode{}
    q = append(q, root)
    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        // 访问 cur 节点
        fmt.Println(cur.Val)
        
        // 把 cur 的左右子节点加入队列
        if cur.Left != nil {
            q = append(q, cur.Left)
        }
        if cur.Right != nil {
            q = append(q, cur.Right)
        }
    }
}

var levelOrderTraverse = function(root) {
    if (root === null) {
        return;
    }
    var q = [];
    q.push(root);
    while (q.length !== 0) {
        var cur = q.shift();
        // 访问 cur 节点
        console.log(cur.val);

        // 把 cur 的左右子节点加入队列
        if (cur.left !== null) {
            q.push(cur.left);
        }
        if (cur.right !== null) {
            q.push(cur.right);
        }
    }
}

写法二

对上面的解法稍加改造，就得出了下面这种写法：

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    // 记录当前遍历到的层数（根节点视为第 1 层）
    int depth = 1;

    while (!q.isEmpty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // 访问 cur 节点，同时知道它所在的层数
            System.out.println("depth = " + depth + ", val = " + cur.val);

            // 把 cur 的左右子节点加入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
        depth++;
    }
}

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    queue<TreeNode*> q;
    q.push(root);
    // 记录当前遍历到的层数（根节点视为第 1 层）
    int depth = 1;

    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();
            // 访问 cur 节点，同时知道它所在的层数
            cout << "depth = " << depth << ", val = " << cur->val << endl;

            // 把 cur 的左右子节点加入队列
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
        depth++;
    }
}

from collections import deque

def levelOrderTraverse(root):
    if root is None:
        return
    q = deque()
    q.append(root)
    # 记录当前遍历到的层数（根节点视为第 1 层）
    depth = 1

    while q:
        sz = len(q)
        for i in range(sz):
            cur = q.popleft()
            # 访问 cur 节点，同时知道它所在的层数
            print(f"depth = {depth}, val = {cur.val}")

            # 把 cur 的左右子节点加入队列
            if cur.left is not None:
                q.append(cur.left)
            if cur.right is not None:
                q.append(cur.right)
        depth += 1

func levelOrderTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []*TreeNode{root}
    // 记录当前遍历到的层数（根节点视为第 1 层）
    depth := 1

    for len(q) > 0 {
        // 获取当前队列长度
        sz := len(q)
        for i := 0; i < sz; i++ {
            // 弹出队列头
            cur := q[0]
            q = q[1:]
            // 访问 cur 节点，同时知道它所在的层数
            fmt.Printf("depth = %d, val = %d\n", depth, cur.Val)

            // 把 cur 的左右子节点加入队列
            if cur.Left != nil {
                q = append(q, cur.Left)
            }
            if cur.Right != nil {
                q = append(q, cur.Right)
            }
        }
        depth++
    }
}

var levelOrderTraverse = function(root) {
    if (root === null) {
        return;
    }
    let q = [];
    q.push(root);
    // 记录当前遍历到的层数（根节点视为第 1 层）
    let depth = 1;

    while (q.length !== 0) {
        let sz = q.length;
        for (let i = 0; i < sz; i++) {
            let cur = q.shift();
            // 访问 cur 节点，同时知道它所在的层数
            console.log("depth = " + depth + ", val = " + cur.val);

            // 把 cur 的左右子节点加入队列
            if (cur.left !== null) {
                q.push(cur.left);
            }
            if (cur.right !== null) {
                q.push(cur.right);
            }
        }
        depth++;
    }
};

注意代码中的内层 for 循环：

int sz = q.size();
for (int i = 0; i < sz; i++) {
    ...
}

这个变量 i 记录的是节点 cur 是当前层的第几个，大部分算法题中都不会用到这个变量，所以你完全可以改用下面的写法：

int sz = q.size();
while (sz-- > 0) {
    ...
}

这个属于细节问题，按照自己的喜好来就行。

但是注意队列的长度 sz 一定要在循环开始前保存下来，因为在循环过程中队列的长度是会变化的，不能直接用 q.size() 作为循环条件。

这种写法就可以记录下来每个节点所在的层数，可以解决诸如二叉树最小深度这样的问题，是我们最常用的层序遍历写法。

写法三

既然写法二是最常见的，为啥还有个写法三呢？因为要给后面的进阶内容做铺垫。

现在我们只是在探讨二叉树的层序遍历，但是二叉树的层序遍历可以衍生出 多叉树的层序遍历，图的 BFS 遍历，以及经典的 BFS 暴力穷举算法框架，所以这里要拓展延伸一下。

回顾写法二，我们每向下遍历一层，就给 depth 加 1，可以理解为每条树枝的权重是 1，二叉树中每个节点的深度，其实就是从根节点到这个节点的路径权重和，且同一层的所有节点，路径权重和都是相同的。

那么假设，如果每条树枝的权重和可以是任意值，现在让你层序遍历整棵树，打印每个节点的路径权重和，你会怎么做？

这样的话，同一层节点的路径权重和就不一定相同了，写法二这样只维护一个 depth 变量就无法满足需求了。

写法三就是为了解决这个问题，在写法一的基础上添加一个 State 类，让每个节点自己负责维护自己的路径权重和，代码如下：

class State {
    TreeNode node;
    int depth;

    State(TreeNode node, int depth) {
        this.node = node;
        this.depth = depth;
    }
}

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<State> q = new LinkedList<>();
    // 根节点的路径权重和是 1
    q.offer(new State(root, 1));

    while (!q.isEmpty()) {
        State cur = q.poll();
        // 访问 cur 节点，同时知道它的路径权重和
        System.out.println("depth = " + cur.depth + ", val = " + cur.node.val);

        // 把 cur 的左右子节点加入队列
        if (cur.node.left != null) {
            q.offer(new State(cur.node.left, cur.depth + 1));
        }
        if (cur.node.right != null) {
            q.offer(new State(cur.node.right, cur.depth + 1));
        }
    }
}

class State {
public:
    TreeNode* node;
    int depth;

    State(TreeNode* node, int depth) : node(node), depth(depth) {}
};

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    queue<State> q;
    // 根节点的路径权重和是 1
    q.push(State(root, 1));

    while (!q.empty()) {
        State cur = q.front();
        q.pop();
        // 访问 cur 节点，同时知道它的路径权重和
        cout << "depth = " << cur.depth << ", val = " << cur.node->val << endl;

        // 把 cur 的左右子节点加入队列
        if (cur.node->left != nullptr) {
            q.push(State(cur.node->left, cur.depth + 1));
        }
        if (cur.node->right != nullptr) {
            q.push(State(cur.node->right, cur.depth + 1));
        }
    }
}

class State:
    def __init__(self, node, depth):
        self.node = node
        self.depth = depth

def levelOrderTraverse(root):
    if root is None:
        return
    q = deque()
    # 根节点的路径权重和是 1
    q.append(State(root, 1))

    while q:
        cur = q.popleft()
        # 访问 cur 节点，同时知道它的路径权重和
        print(f"depth = {cur.depth}, val = {cur.node.val}")

        # 把 cur 的左右子节点加入队列
        if cur.node.left is not None:
            q.append(State(cur.node.left, cur.depth + 1))
        if cur.node.right is not None:
            q.append(State(cur.node.right, cur.depth + 1))

type State struct {
    node  *TreeNode
    depth int
}

func levelOrderTraverse(root *TreeNode) {
    if root == nil {
        return
    }
    q := []State{{root, 1}}

    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        // 访问 cur 节点，同时知道它的路径权重和
        fmt.Printf("depth = %d, val = %d\n", cur.depth, cur.node.Val)

        // 把 cur 的左右子节点加入队列
        if cur.node.Left != nil {
            q = append(q, State{cur.node.Left, cur.depth + 1})
        }
        if cur.node.Right != nil {
            q = append(q, State{cur.node.Right, cur.depth + 1})
        }
    }
}

function State(node, depth) {
    this.node = node;
    this.depth = depth;
}

var levelOrderTraverse = function(root) {
    if (root === null) {
        return;
    }
    // @visualize bfs
    var q = [];
    // 根节点的路径权重和是 1
    q.push(new State(root, 1));

    while (q.length !== 0) {
        var cur = q.shift();
        // 访问 cur 节点，同时知道它的路径权重和
        console.log("depth = " + cur.depth + ", val = " + cur.node.val);

        // 把 cur 的左右子节点加入队列
        if (cur.node.left !== null) {
            q.push(new State(cur.node.left, cur.depth + 1));
        }
        if (cur.node.right !== null) {
            q.push(new State(cur.node.right, cur.depth + 1));
        }
    }
};

这样每个节点都有了自己的 depth 变量，是最灵活的，可以满足所有 BFS 算法的需求。但是由于要额外定义一个 State 类比较麻烦，所以非必要的话，用写法二就够了。

其实你很快就会学到，这种边带有权重的场景属于图结构算法，在之后的 BFS 算法习题集 和 dijkstra 算法 中，才会用到这种写法。

其他遍历？

二叉树的遍历方式只有上面两种，也许有其他的写法，但都是表现形式上的差异，本质上不可能跳出上面两种遍历方式。

比方说，你可能看到用栈来迭代遍历二叉树的代码。但这本质还是是递归遍历，只不过他手动维护栈模拟递归调用罢了。

再比如，你还可能看到递归地一层层遍历二叉树的代码。但这本质还是层序遍历，只不过他把层序遍历代码中的 for 循环用递归的形式展现了。

总之，不要被表象迷惑，二叉树的遍历方式就上面两种，结合后面的教程和习题，你把这两种遍历方式玩明白，一切暴力穷举算法都小菜一碟。